
- •Cборник индивидуальных заданий по высшей математике
- •Творческие задания по теме «Предел»
- •Дополнительные задачи на пределы
- •Задачи на пределы (3й уровень)
- •26-36 Построить графики функций
- •Задачи третьего уровня сложности по теме «пределы»
- •Тема 2. Производная и дифференциал Задания уровня а
- •Задания уровня в
- •Условия заданий по теме 2
- •Ответы на задания по теме 2
- •Тема 3. Неопределенные интегралы Вычислить интегралы
- •Ответы на задания по теме 2
- •Тема 4. Определенные интегралы Задания уровня а
- •Задания уровня b
- •Условия заданий по теме 4
- •Ответы на задания по теме 3
Ответы на задания по теме 2
Вариант 1А
1.
 .2.
.2.
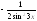 .
.
4.
 .5.
.5.
 .
.
6.
 .7.
.7.
 .
.
8.
 ,
, .10.
.10.
 .
.
Вариант 1В
1.
 3.
1,980.
3.
1,980.
4.

5.
б)
 6.Max=
6.Max= ,Min=
,Min= .
.
7.
 8.
8.

10.

Вариант 2А
1.
 . 2.
. 2. .
.
4.
 . 5.
. 5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 ,
,
 .10.
.10.
 .
.
Вариант 2В
1.
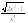 3.
2,010.
3.
2,010.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
3. 8.
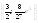

10.
Вариант 3А
1.
 . 2.
. 2.
 .
.
4.
 . 5.
. 5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 ,
,
 .10.
.10.
 .
.
Вариант 3В
1.
 3.
3.

4.


5.
б)
 . 6.
Max=
. 6.
Max=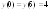 ,
,
Min= .
.
7.
1. 8.

10.

Вариант 4А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 . 10.
. 10.
 .
.
Вариант 4В
1.
 3.
3,020.
3.
3,020.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
 8.
нет.
8.
нет.
10.
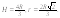
Вариант 5А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
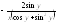 . 7.
. 7.
 .
.
8.
 ,
, .10.
.10.
 .
.
Вариант 5В
1.
 . 3.
0,080.
. 3.
0,080.
4.

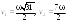
5.
б)
 . 6.
Max=
. 6.
Max=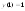 ,
,
Min= .
.
7.
 . 8.
. 8.
 .
.
10. S=2ab.
Вариант 6А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 ,
,
 .10.
.10.
 .
.
Вариант 6В
1.
 3.
3.

4.


5.
б)
 . 6.Max=
. 6.Max= ,
,
Min= .
.
7.
0. 8.
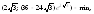

10.
Вариант 7А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 ,
,
 .10.
.10.
 .
.
Вариант 7В
1. . 3.
2,98.
. 3.
2,98.
4.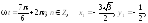

5.
б)
 . 6.
Max=
. 6.
Max= ,
,
Min=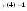 .
.
7.
0,5. 8.

10.
Вариант 8А
1.
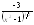 . 2.
. 2.
 .
.
4.
 . 5.
. 5.
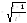 .
.
6. . 7.
. 7.
 .
.
8.
нет. 10.
 .
.
Вариант 8В
1.
 3.
2,975.
3.
2,975.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
 . 8.
. 8.

 и
и


10.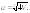
Вариант 9А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6. .
7.
.
7.
 .
.
8.
 ,
,
 .10.
.10.
 .
.
Вариант 9В
1. 3.
1,231.
3.
1,231.
4.

5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
0,18. 8.

10.
Вариант 10А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
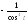 .
.
6.
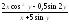 . 7.
. 7.
 .
.
8.
 . 10.
. 10.
 .
.
Вариант 10В
1. 3.
1,07.
3.
1,07.
4.

5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
 8.
8.

10.
 .
.
Вариант 11А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 ,
,
 .10.
.10.
 .
.
Вариант 11В
1. 3.
0,958.
3.
0,958.
4.
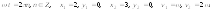
5.
б)
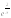 . 6.
Min=
. 6.
Min= ,Max=
,Max= .
.
7.
 .
8.
.
8.


10.

Вариант 12А
1.
 . 2.
. 2.
 .
.
4.
 . 5.
. 5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 ,
,
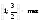 .10.
.10.
 .
.
Вариант 12В
1. 3.
1,02.
3.
1,02.
4.


5.
б)
 . 6.Max=
. 6.Max= ,
,
Min= .
.
7.
 . 8.
. 8.

10.

Вариант 13А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 . 10.
. 10.
 .
.
Вариант 13В
1.
 3.
65,92.
3.
65,92.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7. 1. 8. нет.
10.
Вариант 14А
1. . 2.
. 2. .
.
4.
 5.
5. .
.
6.
 . 7.
. 7.
 .
.
8.
 . 10.
. 10.
 .
.
Вариант 14В
1.
 3.
2,02.
3.
2,02.
4.

5.
б)
 .
6.
Max=
.
6.
Max= ,
,
Min= .
.
7.
 8.
8.
10.
Вариант 15А
1.
 . 2.
. 2.
 .
.
4. 5.
5.
 .
.
6.
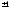 . 7.
. 7.
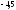 .
.
8. ,
,
 .10.
.10. .
.
Вариант 15В
1. 3.
126,208.
3.
126,208.
4.
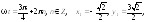

5.
б)
 . 6.Max=
. 6.Max= ,
,
Min= .
.
7.
2. 8.
(1;2,5)-max,

10. 600.
Вариант 16А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 . 10.
. 10.
 .
.
Вариант 16В
1.
 3.
1,97.
3.
1,97.
4.

5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
 8.
8.

10.

 .
.
Вариант 17А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
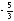 .
.
6. . 7.
. 7.
 .
.
8.
 .10.
.10.
 .
.
Вариант 17В
1. 3.
3,04.
3.
3,04.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min=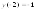 .
.
7.
-3. 8.

10.

Вариант 18А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 . 10.
. 10.
 .
.
Вариант 18В
1.
 3.
0,495.
3.
0,495.
4.

5.
б)
 . 6.
Max=
. 6.
Max= ,
,
Min= .
.
7.
 8.
8.

10.

Вариант 19А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
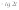 .
.
6.
 . 7.
. 7.
 .
.
8.
 ,
,
 .10.
.10.
 .
.
Вариант 19В
1.
 3.
2,03.
3.
2,03.
4.

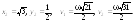
5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
0,25. 8.

10.

Вариант 20А
1.
 . 2.
. 2.
 .
.
4.
 5.
5.
 .
.
6.
 . 7.
. 7.
 .
.
8.
 . 10.
. 10.
 .
.
Вариант 20В
1. 3.
0,49.
3.
0,49.
4.


5.
б)
 6.
Max=
6.
Max=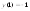 ,Min=
,Min= .
.
7.
1. 8.

10.

Вариант 21А
1.
 2.
2.
 .
.
4.
 5.
5.
 .
.
6.
 7.
5.
7.
5.
8.
 . 10.
. 10.

Вариант 21В
1.
 3.
128,896.
3.
128,896.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,
,
Min= .
.
7.
 . 8.
. 8.

10.
Вариант 22А
1.
 2.
2.

4.
 5.
5.

6.
 7.
7.

8.
 10.
24.
10.
24.
Вариант 22В
1.
 3.
2,03.
3.
2,03.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
 . 8.
. 8.


10.

Вариант 23А
1.
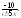 2.
2.

4.
 5.
5.

6.
 7.
7.

8.
 10.
1.
10.
1.
Вариант 23В
1.
 3.
0,97.
3.
0,97.
4.


5.
б)
 . 6.Max=
. 6.Max= ,Min=
,Min= .
.
7.
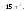 8.
8.


10.

Вариант 24А
1.
 2.
2.

4.
 5.
5.

6.
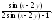 7.
7.
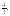
8. 10.
3.
10.
3.
Вариант 24В
1.
 3.
26,919.
3.
26,919.
4.

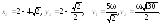
5.
б)
 . 6.
Max=
. 6.
Max= ,
,
Min= .
.
7.
 8.
8.

10.
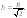
Вариант 25А.
1.
 2.
2.

4.
 5.
5.
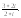
6.
 7.
7.
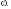
8.
 10.
9.
10.
9.
Вариант 25В
1.
 3.
1,012.
3.
1,012.
4.


5.
б)
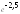 . 6.
Max=
. 6.
Max= ,Min=
,Min=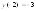 .
.
7.
 8.
8.

10.

Вариант 26А
1.
 2.
2.

4.
 5.
5.

6.
 7.
7.

8. нет. 10. 0,25.
Вариант 26В
1.
 3.
255,488.
3.
255,488.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,Min=
,Min= .
.
7.
 8.
8.

10.

Вариант 27А
1.
 2.
2.

4.
 5.
5.

6.
 7.
7.

8.
 10.
28.
10.
28.
Вариант 27В
1.
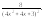 3.
1,01.
3.
1,01.
4.


5.
б)
 6.
Max=
6.
Max= ,
,
Min= .
.
7.
 .8.
нет.
.8.
нет.
10. нет .
Вариант 28А
1.
 2.
2.

4.
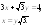 5.
5.

6.
 7.
7.

8.
 10.
2.
10.
2.
Вариант 28В
1.
 3.
1,01.
3.
1,01.
4.


5.
б)
1. 6.
Max= ,Min=
,Min= .
.
7.
 8.
8.


10. нет.
Вариант 29А
1.
 2.
2.

4.
 5.
5.

6. 7.
1,5.
7.
1,5.
8.
 10.
4.
10.
4.
Вариант 29В
1.
 3.
1,01.
3.
1,01.
4.


5.
б) 2. 6.
Max= ,Min=
,Min= .
.
7.
 . 8.
. 8.

10.

Вариант 30А
1.
 2.
2.

4. 5.
5.
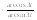
6.
 7.
7.

8.
 10.
3.
10.
3.
Вариант 30В
1.
 3.
2,98.
3.
2,98.
4.


5.
б)
 . 6.
Max=
. 6.
Max= ,
,
Min= .
.
7.
4. 8.

10.

Задачи третьего уровня сложности по теме
«ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ»
№1.
Дано уравнение

где
частота ω>0, а параметр b
удовлетворяет условию:
 .
.
А)
оценить, сколько корней имеет уравнение
в промежутке
 ,
если ω=1, аb=200.
,
если ω=1, аb=200.
Б) оценить интервал, в котором лежат все положительные корни уравнения, как функцию параметра b.
В) сколько всего неотрицательных корней может иметь уравнение в зависимости от величины параметра b, если ω=0?
№2.
Имеет ли положительный корень уравнение:
 ?
?
№3.
Является ли процесс h(t), задаваемый функцией

постоянным? Постройте его график.
№4.
Найти значения первого максимума и первого минимума при t>0 функции
 .
.
Чему равно значение 10-го максимума? Укажите также значения времени t, при которых они достигаются.
№5.
Исследовать зависимость числа неотрицательных корней процесса

от величины постоянных параметров a,k,b.
№6.
Процесс u(t) при t≥0 задан аналитической формулой

где a, b – параметры процесса.
Найти все значения параметров a и b, при которых процесс u(t) имеет первый экстремум при t>0, равный ½.
Чему равно значение b в пункте 1, если a=0.
При каких значениях параметров a и b первый экстремум процесса u(t) при t>0 будет максимумом, а при каких минимумом?
Пусть первый экстремум процесса u(t) равен ½ и достигается при заданном значении времени t=t0>0. Выразите значения параметров a и b через t0.
Найти все значения параметров а и b, при которых процесс u(t) имеет первый максимум (минимум) при t>0 в момент времени t1=
 (t1=
(t1= ).
).
№7.
Докажите, что функция

Дифференцируема
в точке t=0.
Является ли функция f(t)
непрерывно дифференцируемой при всех
значениях t R?
R?
№8.
Найти наибольшее и наименьшее значения функции
 .
.
№9.
Найти
минимум функции
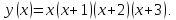
№10.
Сколько действительных корней имеет уравнение
 ?
?
№11.
Найти
все значения параметра q,
при которых график функции
 касается осиOx.
касается осиOx.
№12.
Найти минимум функции и построить ее график
№13.
На
отрезке [a;b]
задана произвольная квадратичная
функция
 .
Чему равна для нее «средняя точка» из
теоремы Лагранжа «о среднем значении»
для отрезка [a;b]?
.
Чему равна для нее «средняя точка» из
теоремы Лагранжа «о среднем значении»
для отрезка [a;b]?
№14.
На
отрезке [x1,x2]
заданы две произвольные квадратичные
функции
 ,
,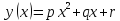 .
.
А) Чему равна для них «средняя точка» С из теоремы Коши для отрезка [x1,x2], если aq≠pb?
Б) Что геометрически для двух парабол f(x) и g(x) выражает условие aq=pb?
В) Чему равно значение С в пункте а), если aq=pb?
№15.
Является ли процесс u(t) , задаваемый аналитической формулой

стационарным (т. е. постоянным во времени)? Постройте график этого процесса.
№16.
Для
функции
 , гдеa,b,c,d
– постоянные действительные коэффициенты
(а≠0) выполняется условие 3ас>b2.
, гдеa,b,c,d
– постоянные действительные коэффициенты
(а≠0) выполняется условие 3ас>b2.
А) Сколько экстремумов может иметь y(x)?
Б) Сколько действительных корней может иметь y(x)?
№17.
Установить общий вид графика функции y(x), производная которой y’(x) имеет вид
 .
.
№18.
Исследовать поведение функции

и нарисовать ее график.
№19.
Вычислить
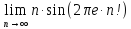 .
.
№20.
Процесс
u(t)
задан формулой
 .
Стремится ли процессu(t)
с ростом t
к некоторому постоянному режиму u1(t)≡c0?
Если «да», то найдите с0
и нарисуйте примерный график u(t).
.
Стремится ли процессu(t)
с ростом t
к некоторому постоянному режиму u1(t)≡c0?
Если «да», то найдите с0
и нарисуйте примерный график u(t).
№21.
Известно,
что
 при некоторыхx,
y.
Верно ли тогда, что
при некоторыхx,
y.
Верно ли тогда, что
 ?
?
№22.
Доказать,
что уравнение
 ,
где а,b,c
– действительные числа и с≠0, имеет не
более трех действительных корней.
,
где а,b,c
– действительные числа и с≠0, имеет не
более трех действительных корней.
№23.
Дано
уравнение
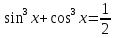 .
.
А)
Сколько корней имеет это уравнение на
отрезке [0; ]?
]?
Б)
Найти все корни, лежащие на отрезке
[0; ].
].
№24.
a,b,c
– длины сторон произвольного тупоугольного
треугольника. Чему равен
 ?
?
№25.
Найти
 .
.
№26.
Исследовать
зависимость числа действительных корней
уравнения
 от величины параметраk
от величины параметраk R.
R.
№27.
Найти
число действительных корней уравнения
 .
.
№28.
Доказать,
что многочлен
 имеет хотя бы один действительный
корень, если
имеет хотя бы один действительный
корень, если .
.
№29.
Доказать, что любой многочлен нечетной степени n (n≥3) имеет хотя бы одну точку перегиба.
№30.
Доказать
что многочлен
 не имеет кратных корней.
не имеет кратных корней.
№31.
Пусть
f(x)
дважды дифференцируема на (0;+∞),
 и
и при
при .
Доказать, что
.
Доказать, что .
.
№32.
Найти
y50(x)
и y(50)(0),
если
 .
.
№33.
Найти
y10(0),
если
 .
.
№34.
Источник
света А расположен на высоте h
над центром круга радиуса а. При каком
значении h
освещенность на границе круга будет
максимальной? (Для освещенности
использовать формулу
 ,
гду с – коэффициент пропорциональности,r
– расстояние от источника до точки, в
которой определяется освещенность,
,
гду с – коэффициент пропорциональности,r
– расстояние от источника до точки, в
которой определяется освещенность,
 – угол наклона луча к плоскости круга
в этой точке).
– угол наклона луча к плоскости круга
в этой точке).
№35.
Докажите, что число е иррациональное.
№36.
Дискретный
процесс {un},
n=1,2,3,…
задается рекуррентной формулой
 где
где ,
а
,
а и
и – два постоянных числа, причем 0<
– два постоянных числа, причем 0< ≤
≤ .
Стремится ли процесс {un}
к некоторому постоянному режиму?
.
Стремится ли процесс {un}
к некоторому постоянному режиму?
(указание: Докажите, что последовательность {un} убывающая и ограничена снизу)
№37.
Найти
наименьшее расстояние между кривыми
 и
и .
.
№38.
При каких значениях параметра µ графики функций y=ln x и y= xμ имеют только одну общую точку?
№39.
Сколько
действительных корней имеет многочлен
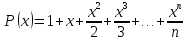 при четном и нечетномn?
при четном и нечетномn?
№40.
Пусть
многочлен P(x)
не имеет действительных коней. Доказать,
что многочлен
 также не имеет действительных корней.
также не имеет действительных корней.
(Указание: примените к P(x) формулу Тейлора)
№41.
Доказать
неравенство
 .
.
№42.
Чему равна наименьшая боковая поверхность прямого кругового конуса объема 1?
№43.
Многочлен
степени n
с действительными коэффициентами
удовлетворяет условию: P(x)≥0
 .
Доказать, что таким же свойством обладает
многочлен
.
Доказать, что таким же свойством обладает
многочлен .
.
№44.
Доказать,
что корни многочлена
 принадлежат отрезку [-1;1] и
принадлежат отрезку [-1;1] и то справедливо неравенство
то справедливо неравенство .
.
№45.
Функция
f(x)
непрерывна на отрезке [0;1] и дифференцируема
на интервале (0;1). Доказать, что если
 ,
то
,
то в некоторой точке
в некоторой точке .
.
№46.
Доказать,
что для любого действительного числа
а
многочлен
 имеет хотя бы один корень в интервале
[-1;1].
имеет хотя бы один корень в интервале
[-1;1].
№47.
Доказать,
что квадратный трехчлен
 при выполнении условий
при выполнении условий ,
, ,
не имеет корней на отрезке [-1;1].
,
не имеет корней на отрезке [-1;1].
№48.
Пусть
 .
Известно, что
.
Известно, что .
.
Докажите,
что
 для любого
для любого .
Укажите также значения коэффициентовa,b,c
и число
.
Укажите также значения коэффициентовa,b,c
и число
 ,
для которых
,
для которых .
.
№49.
Многочлен
P(x)
удовлетворяет функциональному уравнению
 .
Найти все такие многочлены P(x).
.
Найти все такие многочлены P(x).
№50.
Квадратный
трехчлен
 принимает только положительные значения.
Чему равен предел
принимает только положительные значения.
Чему равен предел .
.
№51.
При
каком значении параметра k
передел
 равен 1?
равен 1?
№52.
Является
ли процесс h(t)
затухающим, если
 ?
?
№53.
Найти
все возрастающие функции, удовлетворяющие
условию
 .
.
№54.
Доказать,
что функция
 выпукла в интервале
выпукла в интервале .
.
№55.
Провести полное исследование и построить графики функций
А)

Б)

№56.
Доказать справедливость неравенств:
А)

Б)

В)

Г)

Д)

№57.
Доказать,
что при всех
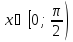 справедливо неравенство:
справедливо неравенство: .
.
№58.
Докажите справедливость неравенств:
А)

Б)

№59.
Вычислите пределы:
А)
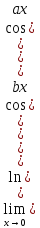
Б)

В)

Г)

№60.
Вычислите предел:

№61.
Построить
кривую, заданную уравнением:
 .
.
№62.
Провести полное исследование и построить графики функций:
А)

Б)

В)
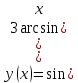
№63.
Существует
ли такая непрерывная на всей вещественной
прямой функция f(x),
что
 для всех
для всех ?
?
№64.
Функция
f(x)
определена на всей вещественной оси.
Известно, что для любого x
и любого h>0
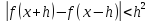 .
Доказать, что
.
Доказать, что .
.
№65.
При
каком значении а функция
 дифференцируема в точкеx=0?
дифференцируема в точкеx=0?
№66.
При
каком значении а функция
 дифференцируема в точкеx=0
?
дифференцируема в точкеx=0
?
№67.
Пусть f(x) – нечетная дифференцируемая на R функция. Доказать, что f’(x) – четная функция. Верно ли обратное утверждение?
№68.
Доказать,
что выражение
 не изменится, если заменитьy(x)
на
не изменится, если заменитьy(x)
на
 .
.
№69.
Непрерывная функция f(x) выпукла вниз и f(0)=0. Доказать, что f(x)/x возрастает при x>0.
№70.
Пусть
f(x)
– дважды дифференцируемая на
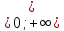 функция и пусть для всехx>0
выполняется неравенство
функция и пусть для всехx>0
выполняется неравенство
 ,
а также неравенство
,
а также неравенство .
.
Доказать,
что
 на
на .
.


