§7. Работа и мощность. Кинетическая энергия

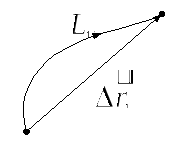
Пусть твердое тело под действием приложенной к нему силы совершает бесконечно малое (элементарное) перемещение (), двигаясь вдоль траектории L,

тогда элементарной работой силыназывается скалярное произведение

,

где - угол между векторамии;- элементарная длина пути перемещения.

При этом ,(т.к- элементарное изменение длины радиус-вектора:, а- модуль элементарного перемещения). Для того, чтобы найти работу на конечном участке траектории, следует просуммировать все элементарные работы, совершаемые силой на всех бесконечно малых участках траектории. Таким образом, мы приходим к сумме бесконечного числа бесконечно малых величин, т.е. интегрированию:

В частном случае, если , и точка движется вдоль прямой (), то работа определяется, где- длина пути.

В системе СИ работа измеряется в Джоулях [Дж].

Опр.

Работа, совершаемая силой за единицу времени, называется мощностью.

Если за время силой была совершена работа, то из определения следует, что.

Мощность измеряется в Ваттах

Для твердого тела, движущегося поступательно, величина называется кинетической энергией. [К] = Дж.

Элементарная работа равнодействующей всех сил равна

Докажем, что (справедливо и для радиус-вектора).

Действительно . Продифференцировав левую и правую части этого тождества, получим.

Тогда

Полученное равенство принято именовать теоремой о кинетической энергии.

Теорема о кинетической энергии

Работа равнодействующей всех сил , приложенных к телу, равна изменению кинетической энергии тела.

Эта теорема верна не только для поступательного движения твердого тела, но и в случае его произвольного движения.

Кинетической энергией обладают только движущиеся тела, поэтому ее называют энергией движения.

§8. Консервативные (потенциальные) силы.

Поле консервативных сил

Опр.

Силы, работа которых не зависит от пути, по которому двигалось тело, а определяется только начальным и конечным положениями тела, называются консервативными (потенциальными) силами.

Опр.

Поле сил – область пространства, в каждой точке которого на тело, помещенное туда, действует сила, закономерно меняющаяся от точки к точке пространства.

Опр.

Поле, не изменяющееся со временем, называется стационарным.

Можно доказать следующие 3 утверждения

1. Работа консервативных сил по любому замкнутому пути равна 0.

Доказательство:

(из определения) , где, т.к. изменение направления на обратное сопровождается заменой всех элементарных перемещений нав интеграле вычисления работы.

2. Однородное поле сил консервативно.

Опр.

Поле называется однородным, если во всех точках поля силы, действующие на тело помещенное туда, одинаковы по модулю и направлению.

Доказательство:

3. Поле центральных сил, в котором величина силы зависит только от расстояния до центра, консервативно.

Опр.

Поле центральных сил – силовое поле, в каждой точке которого на точечное тело, движущееся в нем, действует сила, направленная вдоль линии, проходящей через одну и ту же неподвижную точку – центр поля.

Такое поле определяется координатной зависимостью силы в виде , где - скалярная функция координат.

В общем случае такое поле центральных сил не является консервативным. Если же в поле центральных сил величина силы зависит только от расстояния до центра силового поля (О), т.е. , то такое поле является консервативным (потенциальным).

Доказательство:

где- первообразная.