Физический смысл универсальной газовой постоянной.

У

ниверсальная газовая постоянная имеет размерность работы, отнесенной к 1 молю и температуре 1К.

Выясним физический смысл постоянной “R”.

Пусть в цилиндре под поршнем находится 1 моль газа объема V. Газ под поршнем оказывает давление равное внешнему постоянному давлению, т.е.p=const. Пусть газ в цилиндре нагревается на 1К. Расширяясь, он поднимает поршень на высоту “h”, совершив при том работу, но давление на поршень, поэтому, здесь– приращение объема, т.е., поэтому работа расширения будет равна

(*)

С другой стороны до нагревания уравнение состояния

(1)

после нагревания

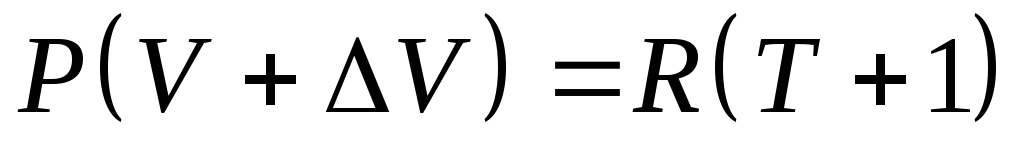
(2)

Вычитая из (2) – (1), получим . Сопоставляя со (*), имеем.

Т.е.

универсальная газовая постоянная численно равна работе при изобарическом расширении 1 моля газа вследствие его нагревания на 1К.

ЗАПОМНИТЬ

ЗАМЕЧАНИЕ: Уравнение Клапейрона – Менделеева справедливо и для смеси газов. Пусть имеем смесь газов:

Массы газов –	m1,m2,m3, …,mn
молярные массы газов –	1,2,3, …,n

Введем величины: ;и т.д. Причем.

Уравнение Менделеева Клапейрона для смеси газов запишется в виде:

.

Для того, чтобы упростить это выражение для смеси газов вводят понятие эффективного молекулярного веса смеси газов.

ОПРЕДЕЛЕНИЕ: Эффективным молекулярным весомназывается вес такого газа, который при одинаковых параметрах со смесью газов имеет ту же массу, что и смесь газов.

; ;

.

9.2. Основное уравнение кинетической теории газов

Если в предыдущем разделе применялся термодинамический метод исследования, то в этом разделе будет использован статистический метод исследования молекулярных процессов. На основании исследования совокупного действия молекул будут получены такие термодинамические параметры, как давление и температура.

Для расчетов воспользуемся моделью идеального газас точки зрения молекулярно-кинетической теории:

молекулы газа непрерывно и хаотично движутся;

молекулы взаимодействуют только во время удара;

удары молекул абсолютно упругие;

размеры молекул малы по сравнению с расстоянием между ними.

Пусть в сосуде кубической формы объемомV = l ³ , гдеl - длина ребра (рис. 9.2), число молекул в единице объема равноn_o. Молекулы движутся хаотично и, соударяясь со стенкой площадьюS=l ², оказывают на нее давление. Результаты расчета давления на стенку не изменятся, если хаотическое движение молекул заменить направленным движением их вдоль осейx, y, z . Тогда со стенкойS будет соударяться третья часть от всех молекул, равная

(9.8)

При каждом соударении со стенкой молекула передает ей импульс, равный mv₁- (-mv₁) = 2mv₁, гдеm- масса молекулы,v₁-ее скорость. За времяt молекула пройдет путьv₁t, соударится со стенкой число раз, равноеv₁t/2l, и передаст стенке импульсP₁=mv₁²t/l. Просуммируем импульс, переданный стенке всемиn молекулами:P =(mt/l)(v₁² +v₂² + ...+v_n²). В данном выражении находится сумма квадратов скоростей. Статистическое усреднение будет заключаться в том, что мы введем новую среднюю величину - среднеквадратичную скорость - по формулеv_кв²=(v₁² +v₂² + ...+v_n²)/n. Следует заметить, чтоv_квприблизительно на 10% больше, чем средняя скорость молекулы, которая определяется по формуле:v_ср=(v₁ +v₂ + ... +v_n)/n. Используя выражение дляv_кв², получимP=mv_кв²tn/l. По второму закону Ньютона на стенку будет действовать силаF = P/t = mv_кв²n/l. Давление газа на стенку найдем по формулеp = F/S = F/l ² илиp = mv_кв²n/l³. Используя формулу (9.8), получим окончательно

(9.9)

Мы получили основное уравнение кинетической теории газов, которое связывает макроскопический параметр - давление газа - с микроскопическими параметрами молекул. Величинаn_o(mv_кв²/2)есть кинетическая энергия молекул, заключенная в единице объема. Отсюда следует, чтодавление есть мера плотности кинетической энергии молекул.

Сравнивая формулы (9.9) и (9.7), получим выражение для средней кинетической энергии молекулы

(9.10)

Итак, мы пришли к важному выводу: кинетическая энергия молекул зависит только от абсолютной температуры. Отсюда следует физический смысл температуры:абсолютная температура есть мера средней энергии поступательного движения молекул. Из формулы (9.10) можно найти среднеквадратичную скорость движения молекул:v_кв² = 3kT/m = 3RT/ . Для кислорода при комнатной температуреv_кв480 м/с и сравнима со скоростью пули.