8.2. Уравнение гармонического колебательного движения.

Пусть на некоторое тело массы “m” действует квазиупругая сила, под действием которой тело приобретает ускорение “a”, тогда поII-закону Ньютонаи, следовательно(пример, колебание шарика, подвешенного к пружинке). Здесь движение (колебательный процесс) происходит вдоль оси “x”.

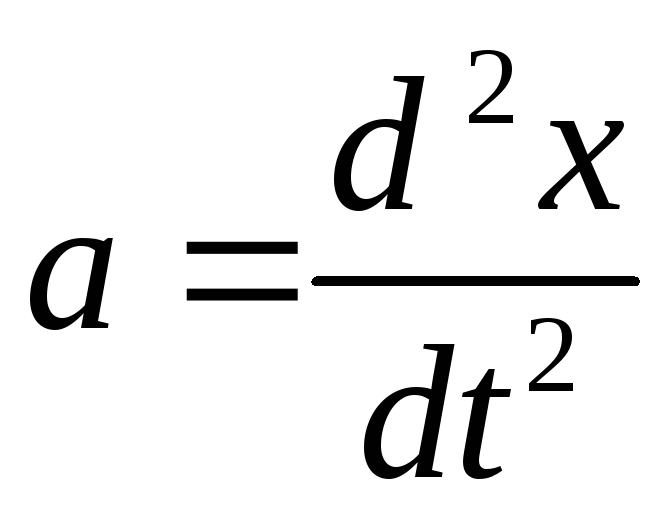Далее ; и; тогдаили.

Колебательный процесс возможен, если коэффициент при “x” положителен, представим его в виде(здесь₀– вещественная величина). Тогда получим:

– дифференциальное уравнение гармонического колебания.

Таким образом, движение шарика на пружинке под действием силы описывается линейным однородным дифференциальным уравнением 2-го порядка.

Решением такого уравнения является функция вида:

, (8.1)

где А – амплитуда колебаний, величина наибольшего отклонения системы от положения равновесия. Определяется величиной первоначального отклонения (А = const> 0).

(₀t+) – фаза колебаний. Физический смысл фазы состоит в том, что она определяет смещение колеблющейся точки в любой момент времени. Постояннаяпредставляет собой значение фазы в момент времениt = 0 и называется начальной фазой колебания. Из уравнения следует, что фазам, отличающимся на величину, кратную 2, соответствуют одинаковые смещения.

Так как смещение системы при колебательном движении представляет периодическую функцию от времени, то и скорость и ускорение такой системы будут также в точности повторяться через равные промежутки времени T, за который фаза колебаний получит приращение, кратное 2. Этот промежуток времениTназывается периодом колебаний (или иначеT– это время, за которое совершается полный цикл колебаний).

(8.2)

С учетом получим

. (8.3)

Из формулы видно, что период колебаний зависит только от свойств самой системы.

Для описания колебательного периодического движения вводится еще несколько величин:

а) – частота колебаний – это величина численно равная числу колебаний в единицу времени.. За единицу частоту (1Гц) принимают частоту такого колебания, период которого равен 1с.

б) ₀= 2– круговая или циклическая частота (₀– число колебаний за 2секунд).

Для колебательного процесса смещение, скорость и ускорение можно представить как аналитически:

1. .

2. .

3. .

т

Рис. 8.2

ак и графически (рис. 8.2).

8.3. Графическое изображение гармонических колебаний. Векторная диаграмма.

Сложение нескольких колебаний одинакового направления (или, что то же самое, сложение нескольких гармонических функций) значительно облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости.

В

Рис. 8.3

озьмем ось, которую обозначим “x”. Из точки О, взятой на оси, под углом, равным начальной фазе колебаний, отложим вектор длиныA(рис. 8.3). Спроектируем векторAна осьx, получимx₀=Acos– начальное смещение колеблющейся точки от положения равновесия. Приведем этот вектор во вращение против часовой стрелки с угловой скоростью₀. Положение этого вектора в любые моменты времени будет характеризоваться углами, равными:

₀t₁+;₀t₂+;₀t₃+; и т.д.

А проекция этого вектора будет перемещаться по оси «x» в пределах от –А до +А. Причем координата этой проекции будет изменяться со временем по закону:

.

Следовательно, проекция конца вектора на некоторую произвольную ось будет совершать гармоническое колебание с амплитудой равной длине вектора, круговой частотой равной угловой скорости вращения вектора и начальной фазой равной углу, образованному вектором с осью в начальный момент времени.

Итак, гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью “x” угол равный начальной фазе колебания.

Р

Рис. 8.4

ассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Смещение колеблющегося тела “x” будет суммой смещенийx₁иx₂, которые запишутся следующим образом:

Представим оба колебания с помощью векторов и(рис. 8.4) По правилам сложения векторов строим результирующий вектор. Проекция этого вектора на осьXбудет равна сумме проекций слагаемых векторов:x=x₁+x₂. Следовательно, векторпредставляет собой результирующее колебание. Этот вектор вращается с той угловой скоростью₀, что и векторыи, так что результирующее движение будет гармоническим колебанием с с частотой₀, амплитудой «а» и начальной фазой. Из построения следует, что

.

Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Этот способ отличается большей простотой и наглядностью, чем использование тригонометрических преобразований.

Проанализируем выражение для амплитуды. Если разность фаз обоих колебаний ₂₁= 0, то амплитуда результирующего колебания равна сумме (а₂+а₁). Если разность фаз₂₁= +или, т.е. колебания находятся в противофазе, то амплитуда результирующего колебания равна.

Если частоты колебаний x₁иx₂неодинаковы, векторыибудут вращаться с различной скоростью. В этом случае результирующий векторпульсирует по величине и вращается с непостоянной скоростью, Следовательно, результирующим движением будет в этом случаенепросто гармоническое колебании, а некоторый сложный колебательный процесс.