Проверка по критерию Фишера

P_мод=1- q₂= FРАСП(1979,82;2;6) =0,999

Показывает, что модель адекватна.

2. Построение экспоненциальной модели. Для построения уравнения нелинейной регрессии вида

= a0 alx

(6.18)

воспользуемся функцией ЛГРФПРИБЛ в Excel, формат ввода аналогичен функции ЛИНЕЙН.

Пример 6.5. Требуется построить модель нелинейной регрессии вида (6.18), используя данные примера 6.1.

1. Введем исходные данные в таблицу Excel(табл. 6.8).

Таблица 6.8. Исходные данные для нелинейной модели

	A	B
1	x	y
2	628	433
3	1577	616
4	2659	900
5	3701	1113
6	4796	1305
7	5926	1488
8	7281	1645
9	9350	1914
10	18807	2411

2. Найдем предельные значения.

	Пределлные значения х1
мин.		628
макс.		18807

2. Построим уравнение регрессии c помощью функции ЛГРФПРИБЛ:

• выделить область 2 столбца и 5 строк (число столбцов равно k+1);

• вызвать функцию ЛГРФПРИБЛ (диапазон у; диапазон х;1;1);

• ввести диапазоны исходных данных ЛГРФПРИБЛ (В2:В10; A2:А10;1;1);

• нажать клавиши Shift + Ctrl + Enter.

Результаты сведены в табл.6.9.

Таблица 6.9. Результаты расчета

	A	B		C
21		Экспоненциальная модель
22		а1	а0
23	Коэффициенты	1,000084	699,7396
24	СКО	2,05E-05	0,164003
25	Достоверн./ Sад.	0,704569	0,319692
26	F / ст.свобод.	16,69419	7
27		1,706195	0,71542

Получаем модель = 699,74  1,000084^x. По критерию Фишера видно, что модель адекватна.

Пример 6.6. Рассмотреть построение нелинейной модели в пакете STATISTICA, используя данные примера 6.1.

1. Запустим пакет STATISTICA и в появившемся окне (рис.3.7) выберем модуль «Множественная регрессия».

2. Откроем исходные данные из примера 6.3 (рис.6.1).

3. Выберем команду «Продолжить анализ», появится окно «Множественная регрессия» (рис. 6.7).

4. Изменим тип регрессии на «Фиксированная нелинейная» и нажмем кнопку «ОК».

Рис.6.7. Окно множественной регрессии для нелинейной модели

5. Появится окно «Регрессия с нелинейными компонентами» (рис.6.8), в котором выберем вид нелинейной функции (например, Х**2). Нажмем кнопку «ОК».

Рис.6.8. Окно для выбора нелинейных компонент

6. Появится окно «Определение модели» (рис.6.9), выберем кнопку «Переменные».

Рис.6.9. Окно настройки модели

7. В окне «Список зависимых и независимых переменных» выберем не только линейные переменные, но и их квадраты (рис.6.10). Нажмем кнопку «ОК».

Рис.6.10. Окно выбора переменных

8. Появится окно «Результаты множественной регрессии» (рис. 6.11). Выберем кнопку «Итоговая таблица регрессии», получим результаты (рис.6.12).

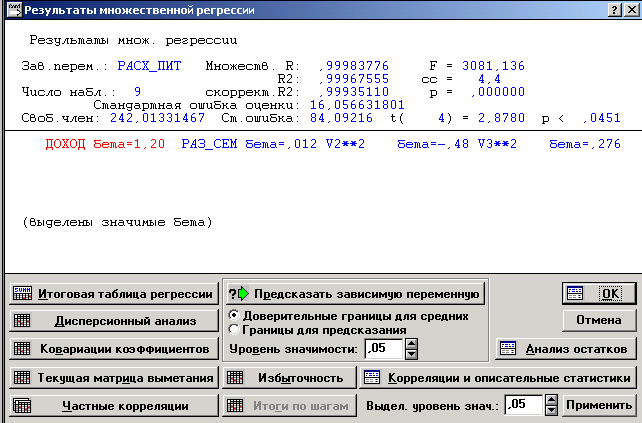
Рис.6.11. Окно результатов множественной регрессии

Рис.6.12. Коэффициенты уравнения нелинейной регрессии

Получаем модель вида

= 242,01 + 0,14x₁ +9,13 x₂ -0,00х₁²+37,50 х₂².

9. Для проверки адекватности выберем команду «Дисперсионный анализ» (рис.6.13).

Критерий Фишера

при минимальном уровне значимости р=0,000, степенях свободы ₁ =4 и ₂=4. Это свидетельствует об адекватности модели.

Рис.6.13. Проверка адекватности нелинейной модели

Аналогичным образом можно построить нелинейную модель другого типа из предлагаемого списка в окне (рис.6.7).