5.2. Применение балансовых моделей

Пример 5.1. Для трех отраслей задана матрица коэффициентов прямых материальных затрат А и конечная продукция Y. Найти коэффициенты полных материальных затрат, валовую Х_j и чистую Z_j продукцию.

Таблица 5.2. Исходные данные расчета межотраслевого баланса

Производящие отрасли	Потребляющие отрасли			Конечная продукция Yi	Валовая продукция Хi
	Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,3	0,1	0,4	200
Отрасль 2	0,2	0,5	0	100
Отрасль 3	0,3	0,1	0,2	300
Условная чистая продукция Zj
Валовая продукция Xj

1. Составим матрицу межотраслевого баланса и запишем исходные данные в матричном виде, т.е. получим матрицы А, Y (табл. 5.2).

Запишем исходные данные в матричной форме:

• матрица коэффициентов прямых материальных затрат

;

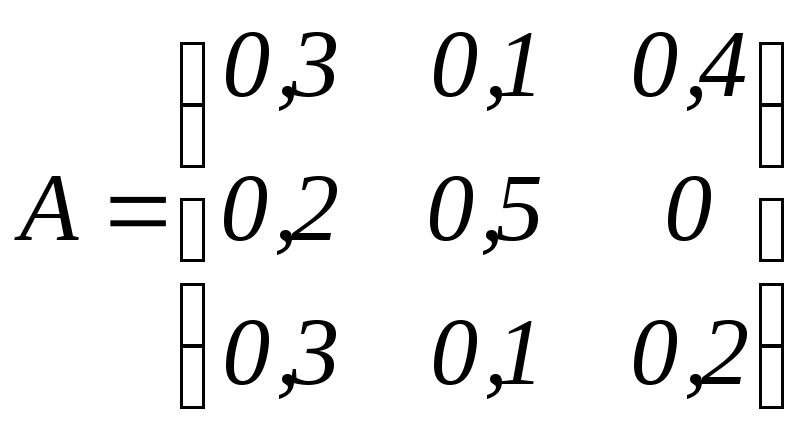• конечная продукция Y =(200 100 300)^Т.

2. Найдем (Е-А), где Е – единичная матрица:

.

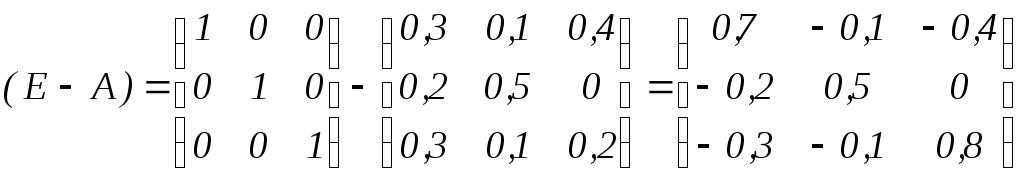3. Вычислим определитель матрицы (Е-А):

.

4. Найдем алгебраические дополнения 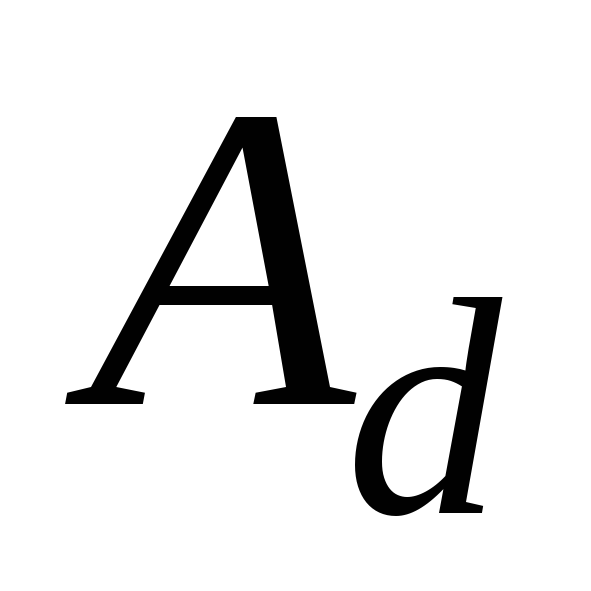для(Е-А):

.

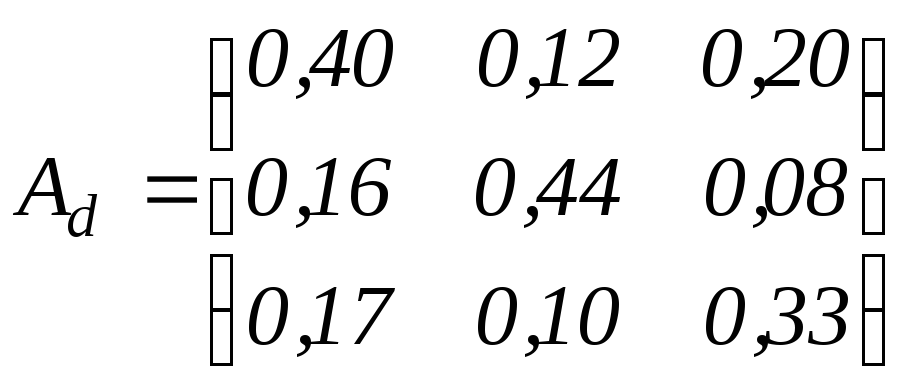5. Вычислим коэффициенты полных затрат:

.

6. Определим величины валовой продукции Х=В·Y=.

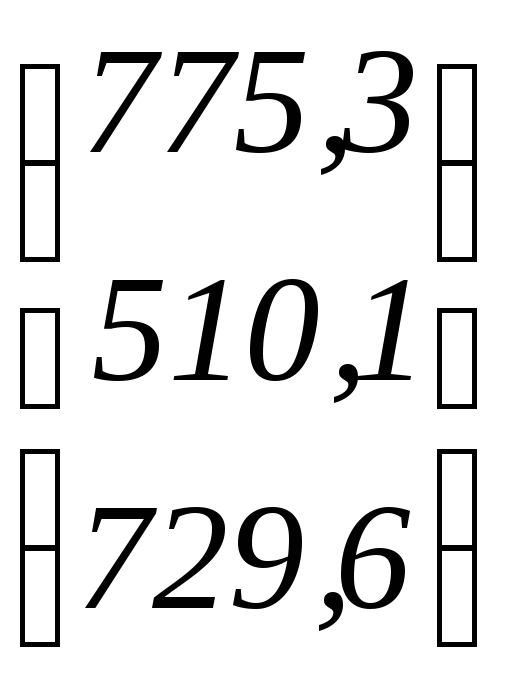7. Определим величины межотраслевых потоков .

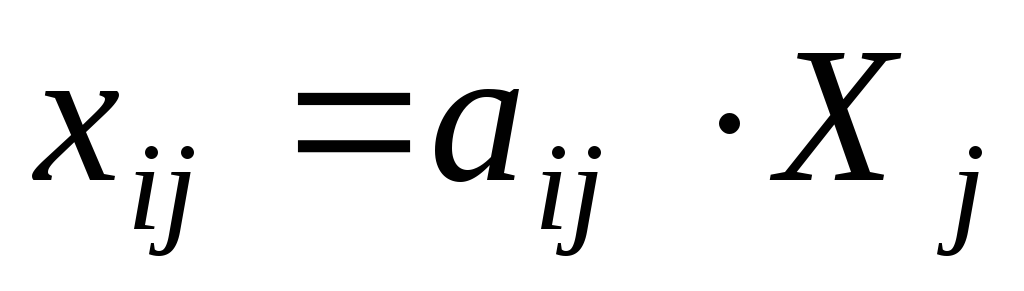8. Рассчитаем величину чистой продукции .

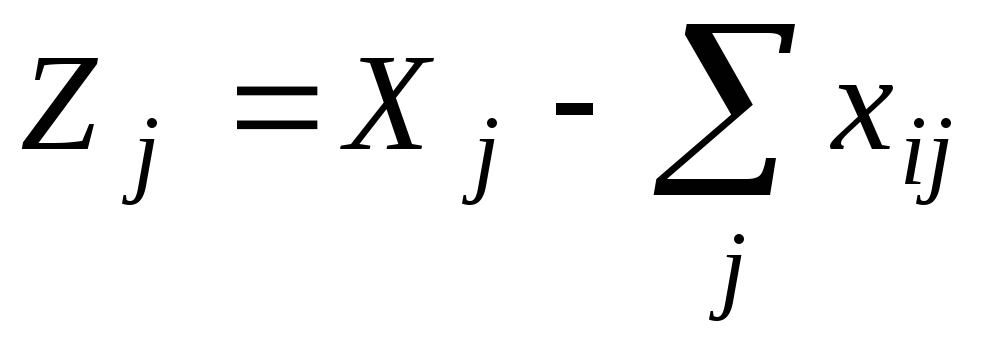Результаты сведены в табл. 5.3.

Таблица 5.3. Результаты расчетов

Производящие отрасли	Потребляющие отрасли			Конечная продукция Yi	Валовая продукция Хi
	Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	232,6	51,0	291,8	200	775,3
Отрасль 2	155,1	0,5255,0	0	100	510,1
Отрасль 3	232,6	0,151,0	145,9	300	729,6
Условная чистая продукция Zj	155,0	153,1	291,9	∑=600
Валовая продукция Xj	775,3	510,1	729,6		∑=2015,0

Пример 5.2. Два цеха предприятия выпускают продукцию двух видов: первый цех – продукцию 1, второй – продукцию 2. Часть продукции идет на внутреннее потребление, остальная часть является конечной продукцией. Требуется выявить распределение между цехами продукции, идущей на внутреннее потребление x_ij, общие (валовые) объемы выпускаемой продукции X_j , если заданы параметры прямых затрат А, и конечной продукции Y (табл.5.4).

Таблица 5.4. Исходные данные для расчета продукции предприятия

Цех	Внутреннее потребление продукции		Конечная продукция Y	Валовая продукция Х
	I	II
I	1/5	1/10	130
II	1/4	1/5	190

Провести расчеты для двух цехов.

Запишем исходные данные в матричной форме:

• матрица коэффициентов прямых материальных затрат

;

• конечная продукция .

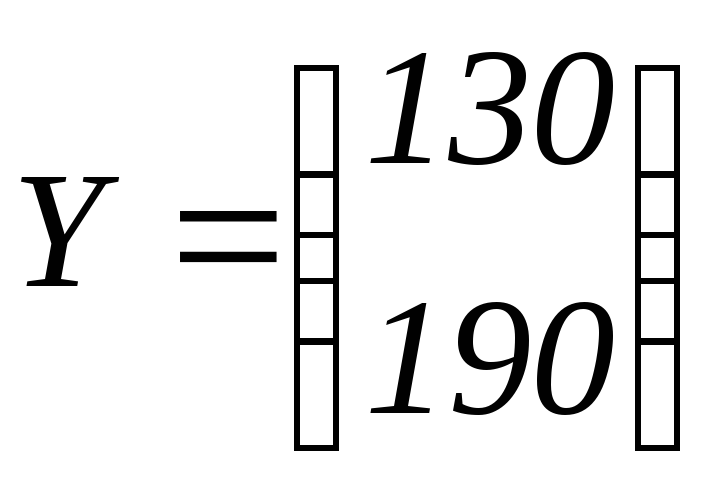Провести расчеты для двух цехов с использованием пакета Excel. Последовательность расчета в электронной таблице Excel ms Office:

1. Создать форму матрицы межотраслевого баланса и ввести исходные данные в таблицу Excel (табл.5.5). Таким образом, записав исходные данные в ячейки таблицы, можем представить их в матричном виде, т.е. получаем матрицы А(B3:C4), Y(D3:D4).

Таблица 5.5. Форма ввода исходных данных

	A	B	C	D	Е
1	Цех	Внутреннее потребление		Конечная продукция Y	Валовая продукция Х
2		I	II
3	I	0,20	0,10	130
4	II	0,25	0,20	190
5	Услов. чистая продукция Zj
6	Валовая продукция Xj

2. Вычислить матрицу (Е-А), введя формулы в ячейки (В7:С8) (табл. 5.6). Получаем результат:

.

3. Рассчитать матрицу B=(Е-А)^-1 с помощью обратной функции МОБР:

• выделить область матрицы В (B10:C11);

• вызвать функцию МОБР и указать диапазон исходных данных (B7:C8);

• нажать клавиши Shift + Ctrl + Enter ;

• в ячейках (B10:C11) получить обратную матрицу

.

Таблица 5.6. Промежуточный расчет

	A	B	C	D	Е
1	Цех	Внутреннее потребление		Конечная продукция Y	Валовая продукция Х
2		I	II
3	I	0,20	0,10	130	=МУМНОЖ(B10:C11;D3:D4)
4	II	0,25	0,20	190	=МУМНОЖ(B10:C11;D3:D4)
5	Услов. чистая продукция Zj	=B6 - СУММ (B13:B14)	=C6 - СУММ (C13:C14)
6	Валовая продукция Xj	=E3	=E4
7	Е-А	=1-B3	=0-C3
8		=0-B4	=1-C4
9
10	В	=МОБР(B7:C8)	=МОБР(B7:C8)
11		=МОБР(B7:C8)	=МОБР(B7:C8)
12
13	х	=B3*B6	=C3*C6
14		=B4*B6	=C4*C6

4. Определить величины валовой продукции Х=В·Y, используя функцию МУМНОЖ:

• выделить область матрицы X (Е2:Е3);

• вызвать функцию МУМНОЖ и указать диапазон исходных данных: массив1 – (B10:C11), массив 2– (D3:D4);

• нажать клавиши Shift + Ctrl + Enter.

В ячейках (Е2:Е3) получим величины валовой продукции:

.

5. Определить величины межотраслевых потоков 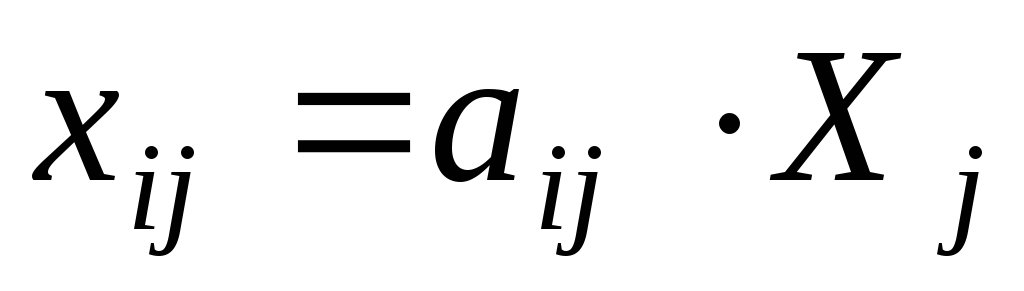(см..табл.5.5):

• в ячейку (В6) записать значение ячейки (Е3), в ячейку (С6) записать значение ячейки (Е4);

• в ячейки х (В13:С15) записать формулы вычисления межотраслевых потоков (см.табл.5.6).

Получим численные значения межотраслевых потоков:

.

6. Рассчитать величину чистой продукции 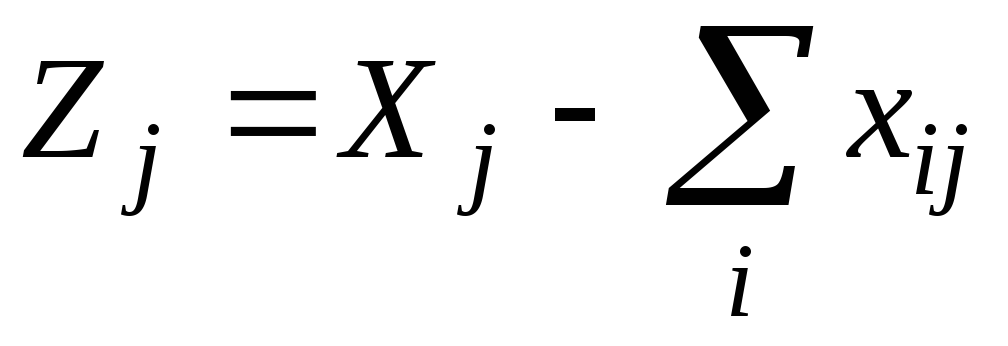, введя в ячейки (В5:С5) соответствующую формулу (табл.5.6).

Получаем значения величин чистой продукции для каждого цеха

.

Результаты расчета можно сгруппировать в виде табл.5.7.

Таблица 5.7. Результаты расчета

	A	B		C	D	Е
1	Цех	Внутреннее потребление			Конечная продукция Y	Валовая продукция Хi
2		I	II
3	I	40	30		130	200
4	II	50	60		190	300
5	Услов.чистая продукция Zj	110	210
6	Валовая продукция Xj	200	300			∑=500

Таким образом, мы получили информацию, которая может быть использована при составлении плана выпуска продукции.

Задания для самостоятельной работы

Задание 1. Для трех отраслей задана матрица коэффициентов прямых материальных затрат А и конечная продукция Y. На основании данных, приведенных в табл.5.8, найти коэффициенты полных материальных затрат, валовую Х_j и чистую Z_j продукцию.

Таблица 5.8. Исходные данные расчета межотраслевого баланса

Производящие отрасли	Потребляющие отрасли			Конечная продукция Yi
	Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,2	0,2	0,1	50
Отрасль 2	0,5	0,3	0,2	0
Отрасль 3	0,2	0,2	0,4	30

Задание 2. Составить задачу, аналогичную приведенным примерам, и решить ее.

Контрольные вопросы

1. 1.Что включает промежуточный и конечный продукт?

2. Из каких частей состоит матрица межотраслевого баланса, что характеризуют эти части?

3. Дайте понятие чистой продукции.

4. Что показывают коэффициенты полных материальных затрат?

5. Для каких задач используются балансовые модели? Приведите примеры их применения.