6.4. Обработка результатов пфэ

при дублировании опытов

Чтобы иметь возможность осуществить проверку адекватности модели и оценить значимость полученных коэффициентов опыта в соответствии с матрицей плана эксперимента, необходимо проводить серии с определенным количеством однотипных измерений в каждой серии опытов. Рассмотрим пример полного факторного эксперимента с двумя уровнями. Таблица с матрицей плана и результатами эксперимента приведена ниже (табл. 6.6).

Таблица 6.6. Форма плана и записи результатов наблюдений ПФЭ

Опыт	z0	z1	z2	z1 z2	Y1	Y2	…	Yi	Ym
1	+	–	–	+
2	+	+	–	–	…	…	…
3	+	–	+	–
4	+	+	+	+		…	…

После составления матрицы плана аналогично табл. 6.6 и проведения эксперимента следует построить уравнение регрессии и проверить его адекватность.

Обработка эксперимента имеет определенную последовательность.

1. Вычисление средних значений для каждого опыта. Определим их по результатам обработки дублированных измерений:

.

(6.20)

2. Вычисление дисперсии для каждого опыта, определяющей разброс наблюдений при фиксированных значениях факторов:

.

(6.21)

Эти значения будут использованы для оценки воспроизводимости, которая покажет, насколько велико влияние помех или факторов, не учтенных в нашем эксперименте.

3. Оценка однородности этих дисперсий. Если проверка однородности будет успешна, то это будет означать, что условия проверки каждой серии опытов не изменялись. Иначе необходимо будет принять, что помимо выбранных нами факторов имеет влияние третий фактор, флуктуация которого приводит к разбросу наблюдаемых откликов. Такой фактор следует включить в эксперимент. Здесь имеется много дисперсий, а для однородности используется критерий Кохрена. Расчетное значение критерия есть отношение максимальной дисперсии из полученных к сумме дисперсий, где n  количество опытов в матрице плана эксперимента:

.

(6.22)

Полученное значение сопоставляется с критическим (табличным), выбранным для определенного уровня значимости и степеней свободы:

.

Если расчетное значение будет меньше критического, то дисперсии будут однородны. Тогда воспроизводимость серии опытов считается доказанной.

4. Принятие в качестве дисперсии воспроизводимости средней из них:

.

(6.23)

Далее эта величина может быть использована для определения значимости коэффициентов регрессии.

5. Вычисление коэффициентов уравнения регрессии:

; i  l.

(6.24)

6. Проверка значимости коэффициентов. В качестве расчетного значения выбирается величина

(6.25)

где  дисперсия оценки коэффициента b;

среднеквадратичное отклонение оценки b.

Полученные значения сопоставляются с критическим . Значения коэффициентов регрессии, для которых t_i меньше критического, могут быть исключены из рассмотрения, так как их влияние сопоставимо с влиянием случайной величины. Таким образом, в уравнении регрессии оказываются только те коэффициенты, которые значимы.

7. Проверка адекватности модели. Она проводится определением разности квадратов между найденным по уравнению и средними значениями для каждого опыта с числом степеней свободы (n – k), где k  количество коэффициентов регрессии, оставшихся в уравнении. Дисперсия адекватности определяется по формуле

.

(6.26)

Полученная дисперсия адекватности сопоставляется с дисперсией воспроизводимости:

(6.27)

Полученное соотношение сравнивается с табличным значением критерия Фишера, для которого степени свободы: ₁= n – k и ₂= n(m– 1) .

Если отношение адекватности меньше критического (F < F_кр), то модель считается адекватной. В противном случае следует рассмотреть более сложную модель.

Пример 6.3. Проведен эксперимент на математической модели в соответствии с матрицей плана табл. 6.6. Результаты эксперимента приведены в табл. 6.7. Требуется построить регрессионное уравнение и проверить его адекватность.

Таблица 6.7. Исходные данные к примеру 6.3

Опыт	z0	z1	z2	z1 z2	y1	y2	y3	y4	y5
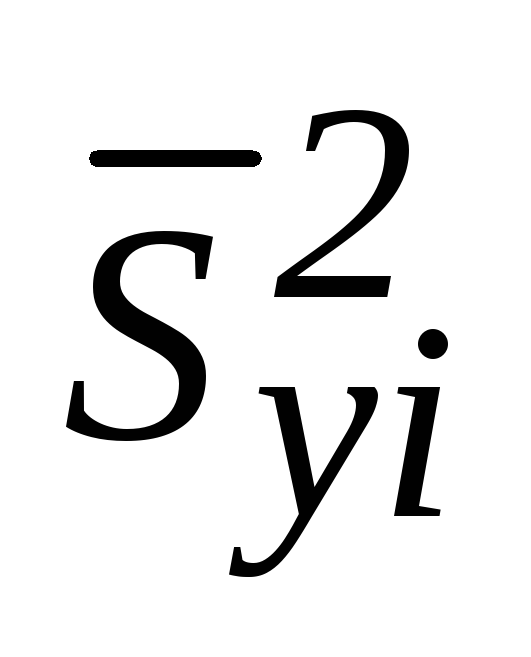
1	+	–	–	+	99,54	98,14	97,78	98,56	99,7	98,74	0,719
2	+	+	–	–	130,8	130,5	135,15	132,1	134,49	132,62	4,494
3	+	–	+	–	190,07	193,52	195,88	193,53	193,62	193,32	4,323
4	+	+	+	+	165,09	161,67	159,66	163,2	159,42	161,81	5,761

Решение.

1. Вычислим средние значения для каждого опыта, определив их по результатам обработки дублированных измерений по формуле (6.20), и занесем в табл. 6.7.