Дисперсия времени отказа
|
|
(2.44) |
,при условии = const
|
|
(2.45) |
,откуда
|
|
(2.46) |
.
Следовательно,
при экспоненциальном
законе надежности
среднее квадратичное отклонение времени
отказа равно среднему времени безотказной
работы. Это свойство экспоненциального
закона надежности позволяет считать,
что при его наличии величина
является достаточно полной характеристикой
надежности.
Для определения
характеристик надежности элементов
проводят специальные испытания при
условиях, близких к условиям функционирования
этих элементов в системе. При этом
исследуется N
образцов
элемента. На временной шкале откладываются
равные интервалы времени t.
В каждом i-м
интервале времени определяется число
отказавших элементов
.
Испытания продолжаются до тех пор
,
пока не выйдут из строя все элементы.
Среднее время безотказной работы на основании опытных данных определяют по формуле
|
|
(2.47) |
,где
.
Статистическая оценка (t) получается из выражения
|
|
(2.48) |
,где
n
число отказавших элементов за промежуток
времени от
;
среднее число
исправно работающих элементов в интервале
t
(
число исправно работающих элементов в
начале и конце интервала).
Вышеприведенные характеристики являются показателями надежности невосстанавливаемых объектов. При этом не учитывается возможность их восстановления в процессе функционирования системы. В практических условиях такая возможность чаще всего присутствует; более того, для этих целей создаются специальные службы.
Полагая,
что каждый отказ каким-либо способом
устраняется, восстанавливаемый элемент
можно характеризовать числом отказов
n,
происходящих
в течение промежутка времени t,
и средним временем между двумя соседними
отказами
,
называемымнаработкой
на отказ.
|
|
(2.49) |
,где n число отказов элемента за время испытаний t;
время
исправной работы элемента между (i
–1)-м
и i-м
отказами.
Если испытания производились не с одним, а с m аналогичными элементами, то
|
|
(2.50) |
,где
число отказов j-го
образца;
время исправной работы между (i
– 1)-м и i-м
отказами j-го
образца.
Пример 2.5. На основании данных технических паспортов установлено, что вероятность отказа прибора 1 в течение 6000 ч составляет 0,95, а вероятность отказа прибора 2 в течение 10000 ч – 0,90. Определить, какой из этих приборов более надежен.
Решение. В соответствии с (2.30) вероятность безотказной работы приборов за соответствующие периоды времени следующая:
На основании (2.43) имеем
.
Отсюда
.
Для прибора 1
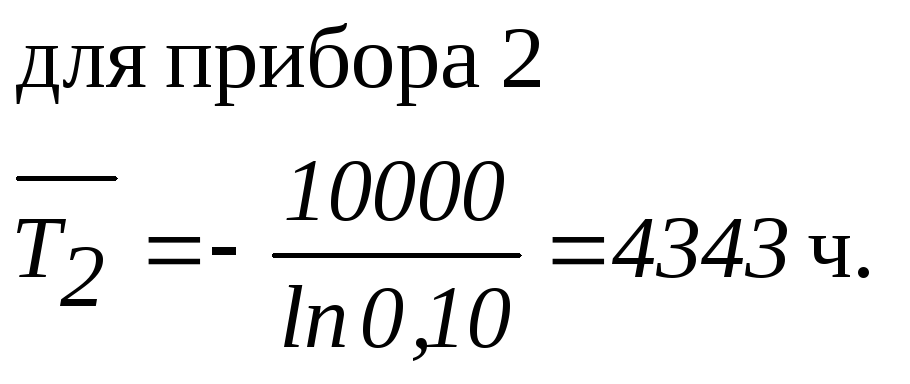
Поскольку
,
можно считать, что прибор 2 более чем в
два раза надежнее прибора 1.
Пример 2.6. На основании проведенных испытаний N образцов элемента А получены следующие результаты (табл.2.1).
Таблица 2.1. Результаты испытаний
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
2 |
11 |
23 |
40 |
56 |
66 |
75 |
81 |
79 |
69 |
53 |
45 |
25 |
18 |
11 |
6 |
Здесь
i
– номер
интервала испытаний,
– число
отказавших образцов на i-м
интервале времени. Общее число образцов
элемента А
определяется как
.
В нашем примереN
= 660. Длительность
интервала t
= 200 ч. Следует
определить среднее время безотказной
работы.
Решение. По (2.47) получим
Задания для самостоятельной работы
1. На основании данных испытаний, приведенных в примере 2.6, определите:
функцию плотности вероятности f(t);
функцию распределения F(t) = Q(t);
функцию вероятности безотказной работы P(t);
вероятность
безотказной работы P(t)
для какого-то
значения t
= Т
по графику функции P(t)
и аналитически на основании полученного
.
2. В офисе работают 25 секретарей, которые постоянно пользуются ручкой и карандашом. Среднее время безотказной работы (среднее время износа) ручки 80 ч, карандаша – 140 ч. Сколько приблизительно нужно приобретать офису ручек и карандашей на 1 месяц, если известно, что среднее время (математическое ожидание) пользования ручкой 2 ч/день, карандашом – 0,5 ч/день?