2.3.1. Определение количественных характеристикнадежности элементов

Допустим, что при отсчете времени работы элемента от t = 0 при t = T произойдет отказ. Тогда Т определим как время отказа. Представим P(t) как вероятность того, что в течение времени t  T отказа не произойдет. Р(t) называют вероятностью безотказной работы. Вероятность события, противоположного рассмотренному и несовместимого с ним, когда t  T, называют вероятностью отказа Q(t):

Q(t) = 1 – P(t).

(2.30)

Вероятность безотказной работы P(t) является непрерывной убывающей функцией времени, вид которой (рис.2.2) определяется условиями возникновения отказа в системе, т.е. траекторией (t).

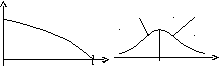
P(t) f(t)

Q(t) P(t)

t t

T t = Т

Рис.2.2. Вероятность безотказной работы

Рис.2.3. Вероятность отказа

Очевидно лишь, что Р(0) = 1, Р () = 0. Тогда из (2.3) следует, что отказ исключен лишь при t = 0, когда P(t) = 1 и Q(t) = 0. Отказ возможен при всех значениях t > 0, хотя при малых t вероятность его мала.

Время отказа как непрерывная случайная величина характеризуется функцией плотности вероятности f(t). При этом вероятность безотказной работы при T  t

,

(2.31)

а вероятность отказа

.

(2.32)

Площадь под кривой f(t) (рис.2.3), равная 1, разделена на две части ординатой, соответствующей абсциссе t. Площадь слева от t численно равна Q(t), а справа  Р(t).

Из (2.32) следует, что вероятность отказа является функцией распределения Т, т.е.

Q(t) = F(t),

(2.33)

тогда

.

(2.34)

Из (2.30) и (2.34) находим

.

(2.35)

Время отказа характеризуется средним из всех значений, которые оно может получать при наблюдении множества однотипных элементов. Среднее время безотказной работы при t  0 есть математическое ожидание¹.

.

(2.36)

Определим средний функциональный ресурс невосстанавливаемых элементов. Если представить, что группа однотипных элементов входит в состав одной системы и отказы в этой группе не устраняются, то интенсивность отказов этих элементов

.

(2.37)

Из (2.37) следует

.

(2.38)

При (t) = const, что соответствует режиму нормального функционирования системы,

,

(2.39)

а

,

(2.40)

т.е. имеет место экспоненциальное распределение времени отказов. Подставляя (2.39) в (2.36), получим

.

(2.41)

Это означает, что постоянная интенсивность отказов  =const равна средней частоте отказов

.

(2.42)

Из (2.40) и (2.42) следует, что

.

(2.43)

Приняв в (2.43) t = , получим , т.е. математическое ожидание времени отказа для экспоненциального распределения определится как время, в течение которого вероятность безотказной работы уменьшится до 0,37, т.е. в е раз.

Среднее время безотказной работы является лишь одной из численных характеристик случайной величины времени безотказной работы Т (наработки). Для исчерпывающей характеристики Т необходимо знать еще и дисперсию времени отказа или его среднее квадратичное отклонение.