Построение статистических регрессионных моделей в ппп statistica
|
Цель работы: |
получить навыки обработки экспериментальных данных в ППП STATISTICA. |
Пример 8. Построение регрессионной модели.
Для исходных данных лабораторной работы № 8 требуется проанализировать зависимость величины расходов на питание от величины душевого дохода и среднего размера семьи. Построим регрессионное уравнение вида у=f(x1,x2). Исходные данные возьмем из табл. 9.
Последовательность выполнения
Для построения уравнения множественной регрессии запустите пакет STATISTICA и откройте файл данных для лабораторной работы №6, содержащий три переменные – РАСХ_ПИТ, ДОХОД, РАЗ_СЕМЬИ и 9 наблюдений.
Выберите в строке команд Статистика/Множественная регрессия, появится окно Multiple Linear Regression (рис.60). Задайтесь переменными: независимыми (independent) – ДОХОД, РАЗ_СЕМЬИ; зависимой (dependent)– РАСХ_ПИТ. Нажмите кнопку ОК.
Рис.60. Окно множественной регрессии
Появится окно результатов Multiple Regression Results (рис.61). Активизировать вкладку Advanced и изучить полученные результаты, выбрав соответствующие кнопки.
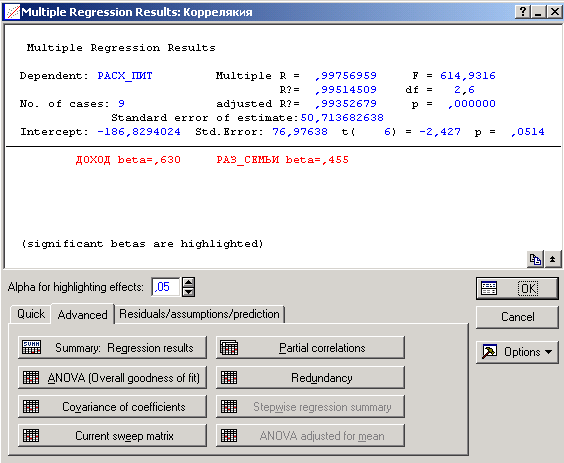
Рис.61. Окно результатов
Выбрав кнопку Summary Regression Results получим коэффициенты модели с проверкой их значимости (рис.62). Таблица результатов включает:
бета коэффициенты;
среднеквадратические отклонения бета;
коэффициенты регрессии В;
среднеквадратические отклонения В;
критерий Стьюдента для каждого коэффициента В;
уровень принятия гипотезы о незначимисти коэффициента В (p-level)
Таким образом, модель имеет вид
,
причем все коэффициенты модели значимы, так как p-level мал.
Рис. 62. Коэффициенты линейной модели
Выбрав кнопку ANOVA (Overall goodness of fit) получим проверку адекватности модели (рис.63). Таблица результатов включает:
суммы квадратов;
степени свободы;
среднеквадратические отклонения;
критерий Фишера;
уровень принятия гипотезы (p-level).
Критерий
Фишера равен
при минимальном уровне значимостир=0,00000
и степенях
свободы 1
=2 и 2=6,
что свидетельствует об адекватности
модели.
Рис.63. Проверка адекватности модели
Нажав кнопку Cancel в окне результатов (рис.61) получим другое окно результатов. Активизируйте вкладку Advanced, поставьте галочку против режима Review descriptive statistics, correlation matrix (рис.64) и нажмите кнопку OK. В появившимся окне нажмите кнопку Correlation, получим матрицу парных коэффициентов корреляции независимых факторов (рис. 65). Нажав кнопку Means & standard deviations получим таблицу средних и СКО для каждой переменной (рис. 66). Для выхода из метода следует нажать кнопку Cancel.
Рис.64. Окно результатов
Рис.65. Корреляционная матрица
Рис. 66. Таблица средних значений и СКО для переменных
Пример 9. Построение регрессионной модели методом шаговой регрессии.
Рассмотрим решение задачи по данным лабораторной работы № 8 (табл.9) методом шаговой регрессии. Исходные данные вводятся аналогично данным регрессионного анализа.