Последовательность выполнения
Запустите пакет STATISTICA 6.0 и в появившемся окне введите исходные данные в файл. При этом файл данных будет содержать три переменные – ГРУППА, НАБЛЮД и ЧИСЛ_ЗАД и 30 наблюдений (5 наблюдений 6 уровней) (рис. 30). Сохраните данные в файле.
Выберите режим Статистика / Непараметрические данные. Появится окно непараметрические статистики Nonparametric Statistics (рис.31), в котором следует выбрать режим Comparing multiple indep. samples (groups) и нажать кнопку ОК.
|
|
|
|
Рис.30. Окно исходных данных |
Рис.31. Окно непараметрической статистики |
Появится окно Kruskal-Wallis ANOVA and Median Test (рис.32). Необходимо задаться зависимой (grouping) переменной (ГРУППА) и зависимой (dependent) переменной (ЧИСЛ_ЗАД), задаться кодами – All. Нажмите кнопку Summary: Kruskal-Wallis ANOVA and Median Test.
|
|
|
Рис.32. Окно дисперсионного анализа Краскела-Уоллиса |
Результаты расчета представлены в двух таблицах (рис. 33 – 34).
Рис.33. Результаты анализа - критерий Краскела-Уоллиса
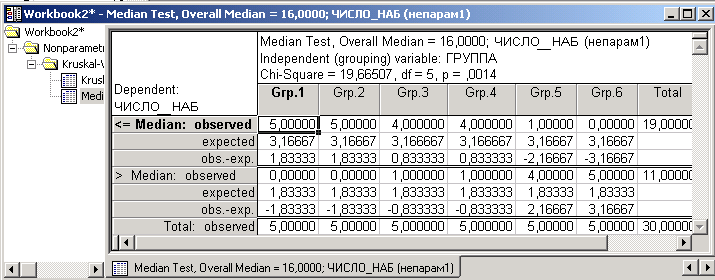
Рис.34. Результаты анализа – Медианный тест, критерий 2
Критерий Краскела-Уоллиса H=21,219 при минимальном уровне значимости р=0,0007. Так как р-уровень близок к нулю, то мы не можем принять гипотезу Н0 и должны ее отвергнуть. Следовательно, денежное стимулирование влияет на производительность труда. Критерий 2=19,665 при минимальном уровне значимости р=0,0014. По этому критерию мы тоже должны отвергнуть гипотезу Н0.
Методика выполнения лабораторной работы
1. Запустить ППП STATISTICA. Ввести данные из лабораторной работы №4. Первый столбец соответствует уровню фактора, второй – наблюдениям. Сохранить данные в файл.
2. Выбрать метод однофакторного анализа аналогично примеру 3 и проверить гипотезу о влиянии фактора на исследуемый процесс.
3. Сравнить с ручным расчетом и сделать выводы.
4. Выбрать непараметрический метод – Краскела-Уоллиса и провести расчеты аналогично примеру 4.
5. Сделать выводы о принятии или отвержении нулевой гипотезы.
Контрольные вопросы
1. Какие методы решают задачи однофакторного анализа в ППП STATISTICA?
2. Какие задачи можно решать с помощью метода однофакторного анализа в ППП STATISTICA?
3. Какие выводы можно сделать на основании полученных результатов обработки?
Лабораторная работа n 6 Двухфакторный дисперсионный анализ
|
Цель pаботы: |
получить навыки в постановке и проверке гипотезы о значимости влияния нескольких факторов на исследуемый отклик |
Постановка статистической задачи
Рассмотpим постановку многофакторной задачи в общем виде.
Дано:
отклик y
может зависить от m
независимых упpавляемых фактоpов
;
каждый фактоp
может ваpьиpоваться на
уpовнях; каждыйj-й
уpовень содеpжит
наблюдений
.
Oпpеделить, в какой меpе существенно на фоне случайных погpешностей (шума) влияние того или иного фактоpа xi на отклик y.
Пусть имеем матpицу наблюдений влияния двух фактоpов x1 и х2 на y (табл.6).
Таблица 6. Наблюдения за откликом y при изменении факторов x1 и x2
-
Уровни фактора х2
Уровни фактора х1
1
...
k1
1
...
...
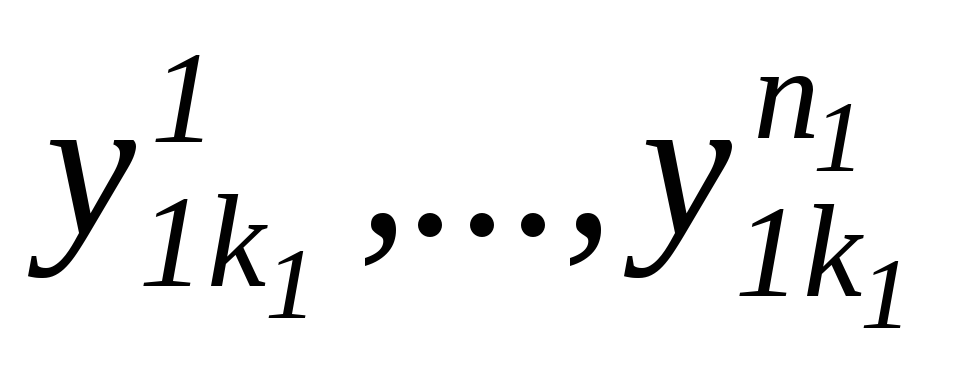
k2
...
Как
видно из таблицы, для каждого уровня
фактора имеем
наблюденийy.
Преобразуем данные, вычислив для каждой
пары уровней переменных х1
и х2
среднее значение наблюдения у:
.
Данные сведем в таблицу (табл.7) и вычислим среднее значение y по каждому уровню и общее среднее по формулам:
.
Таблица 7. Рассчитанные значения
|
Уровни фактора х2 |
Уровни фактора х1 |
Сpеднее
по уровням фактора х1:
| ||
|
1 |
... |
k1 | ||
|
1 |
|
... |
|
|
|
... |
|
|
|
|
|
k2 |
|
... |
|
|
|
Сpеднее
по уровням х2
:
|
|
… |
|
|
