Лабораторная работа n 5

Однофакторный анализ в ППП STATISTICA

Цель работы:

получить навыки проверки гипотезы о значимости влияния фактора на исследуемый отклик с использованием ППП STATISTICA

Пример 3. Однофакторный дисперсионный анализ.

Имеем наблюдения – оценки успеваемости студентов за выполнение лабораторных работ, которые проставляются с точностью до одного знака после запятой. Число лабораторных работ равно 5, число студентов – 8. Требуется установить, влияет ли номер лабораторной работы на оценки студентов, т.е. одинаковы ли по сложности лабораторные работы. Предположим, что плотность распределения оценок соответствует нормальному закону распределения. Исходные данные приведены ниже (табл.4).

Таблица 4.Исходные данные

Студенты (наблюдения)	Лабораторные работы (уровни фактора А)
	ЛАБ1	ЛАБ2	ЛАБ3	ЛАБ4	ЛАБ5
Иванов И.И.	4,0	3,5	4,3	4,0	5,0
Петрова П.П.	4,5	4,6	5,0	4,7	4,0
Сидорова С.Н.	3,0	3,5	4,0	3,6	3,0
Смирнова И.П.	4,3	4,0	4,4	4,5	4,0
Павлова Р.Л.	5,0	4,5	4,0	4,5	5,0
Рыжова Е.П.	3,5	3,3	3,0	4,0	3,5
Гришина Н.В.	2,0	3,0	2,5	3,5	3,0
Шилина Л.В.	4,7	4,0	4,0	4,5	4,2

Выдвинем нулевую гипотезу о том, что сложность работ одинакова и фактор А (номер лабораторной работы) не влияет на оценки, т.е. Н₀ : m₁ = m₂ = .. .= m_k = m. Сделаем необходимые вычисления в пакете STATISTICA.

Последовательность выполнения

1. Запустите пакет STATISTICA 6.0 и в появившемся окне введите исходные данные в файл аналогично тому, как показано в лабораторной работе №1. При этом файл данных будет содержать 2 переменные (ЛАБ_РАБ и НАБЛЮД) и 40 наблюдений ([5лабораторных работ] [8студентов]) (рис.19). Сохраните данные в файле.

2. Выберите режим Статистика /Анализ вариантов (рис.20). Появится окно General ANOVA/MANOVA, где следует выбрать однофакторный дисперсионный анализ One-way ANOVA (рис.21) и нажмите кнопку ОК.

Рис.19. Исходные данные	Рис.20. Меню команды Статистика

Рис.21. Окно выбора метода анализа

3. Появится окно дисперсионного анализа ANOVA/MANOVA One-way ANOVA, в котором следует, нажав кнопку Variables задаться зависимыми Dependent (НАБЛЮД) и независимыми переменными Categorical predictor(factor)) (ЛАБ_РАБ) (рис.22). Нажмите кнопку OK.

4. В окне дисперсионного анализа (рис.23) нажмите кнопку Factor codes. Появится окно Select codes for indep.Var (factors) (рис.24) в котором нажмите кнопку All.

Рис.22. Окно задания переменных для анализа

Рис.23. Окно дисперсионного анализа

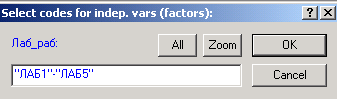
Рис.24. Выбор кодов независимых переменных

5. Нажав кнопку OK, в окне дисперсионный анализ появится окно результатов дисперсионного анализа ANOVA Results 1 (рис.25).

Рис.25. Окно результатов дисперсионного анализа	Рис.26. Таблица эффектов

6. Выберем режим All effects/Graphs, появится таблица эффектов (рис.26), в котором для независимой переменной рассчитаны:

• степени свободы (Dtgr. of Freedom);

• дисперсии фактора (MS);

• критерий Фишера (F);

• уровень принятия гипотезы Н₀ (p-level).

7. Выбрав в этом окне кнопку Graph можно получить графики средних (рис.27), а выбрав режим Spreadsheet получим таблица средних значений по уровням (рис.28).

Рис.27. Графики средних значений по уровням

Рис.28. Таблица средних значений по уровням

8. В окне результатов дисперсионного анализа выберем режим All effects, появится таблица проверки адекватности модели (рис.29).

Рис.29. Таблица проверки адекватности модели

В нашем примере видно, что фактор ЛАБ_РАБ (номер лабораторной работы) имеет F=0,273 и р-уровень (минимальный уровень значимости), равный 0,89. Следовательно, с вероятностью 0,89 можно принять гипотезу Н₀ о равенстве математических ожиданий оценок студентов за выполнение лабораторных работ. Таким образом, можно считать доказанным, что сложность выполнения лабораторных работ примерно одинакова. Из графиков средних и таблиц средних также видно несущественность отличия математических ожиданий.

Пример 4. Однофакторный непараметрический анализ экспериментальных данных.

Рассмотрим решение задачи непараметрического анализа методом Краскела-Уоллиса. Для выяснения влияния денежного стимулирования на производительность труда шести однородным группам из 5 человек были предложены задания одинаковой трудности. Задания предлагались каждому испытуемому независимо от остальных. Группы отличались величиной денежного вознаграждения за решаемую задачу. Данные (число решаемых задач) приведены в табл. 5. Требуется доказать, что производительность труда в каждой группе существенно отличается от остальных. Для доказательства предположения сформулируем гипотезу Н₀ о том, что расхождение наблюдений в каждой группе объясняется только случайными причинами, т.е. величина вознаграждения не влияет на производительность труда.

Таблица 5. Исходные данные

Наблюдения	Уровни
	Гр.1	Гр.2	Гр.3	Гр.4	Гр.5	Гр.6
1	10	8	12	12	24	19
2	11	10	17	15	16	18
3	9	16	14	16	22	27
4	7	13	9	16	18	25
5	13	12	16	19	20	24