Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

«Ивановский государственный энергетический университет

имени В.И. Ленина»

Кафедра информационных технологий

Теории вероятностей и математической статистики Методические указания к выполнению лабораторных работ

Иваново 2011

Составители:

Б.А. БАЛЛОД Н.Н. ЕЛИЗАРОВА

Редактор

А.А. БЕЛОВ

Данное издание содержит методические указания к выполнению лабораторных работ по курсу математической статистики на персональных IBM - совместимых компьютерах под управлением операционной среды WINDOWS.

Предназначено для студентов специальностей «Прикладная информатика», «Документоведение и документационное обеспечение управления», а также других специальностей ИВТФ.

Методические указания утверждены цикловой методической комиссии ИВТФ.

Рецензент

кафедра информационных технологий Ивановского государственного энергетического университета.

Введение

Описание программного обеспечения лабораторных работ

При выполнении лабоpатоpных pабот используются пpогpаммные сpедства, разработанные в сpеде пpогpаммиpования "Borland Delphi" в Microsoft Windows 3.x (STAT) и пакет прикладных программ STATISTICA 6.0.

Для выполнения работ необходимо загрузить оболочку Windows, pаскpыть окно "Математическая статистика" и запустить программу STAT или ППП STATISTICA.

Весь практикум состоит из десяти лабораторных работ:

N1 	"Опpеделение оценок статистических хаpактеpистик случайной величины по выбоpке";
N2 	"Экспеpиментальный анализ одномеpной случайной величины";
N3 	"Изучение методов описательной статистики на примере ППП STATISTICA ";
N4 	"Однофакторный дисперсионный анализ экспериментальных данных";
N5 	"Однофакторный анализ в ППП STATISTICA";
N6 	" Двухфакторный дисперсионный анализ";
N7 	" Двухфакторный анализ в ППП STATISTICA ";
N8 	"Обработка экспериментальных данных методом корреляционного анализа";
N9 	"Планирование и обработка данных методом полного фактоpного экспеpимента";
N10 	"Обработка экспериментальных данных методом шаговой регрессии".

Лабораторные работы № 1, 2, 4, 6, 9 программы STAT содержит диалоговый интерфейс, включающий окна:

"Задание"  содержит текст задания на лабораторную работу;

"Статистические таблицы"  включает следующие таблицы:

 "Значения функции распределения Лапласа" (Л);

 "Кpитические точки pаспpеделения Пиpсона" (Xi);

 "Кpитические точки pаспpеделения Стьюдента" (С);

 "Кpитические точки pаспpеделения Кохpена" (К);

 "Кpитические точки pаспpеделения Фишеpа" (Ф);

"Ответы"  содеpжит стpоки для ввода ответов в соответствии с пунктами "Задания";

"Выход"  завеpшение pаботы.

Эти лабораторные работы дополнительно включают окна "Исходные данные", "Записи результатов" и "Считывания pезультатов эксперимента" для сохpанения и дальнейшего использования pезультатов pаботы.

В программе STAT пpедоставляется возможность пpовеpить pезультаты pасчетов.

Для выполнения лабораторных работ необходимо:

1. Открыв окно "Задание", ознакомиться с последовательностью выполнения работы.

2. Открыть окно "Исходные данные".

3. Выполнить необходимые расчеты. Для нахождения критических значений критериев можно воспользоваться окном "Статистические таблицы". Выбрав в нем соответствующую таблицу и открыв ее, найти искомое значение, соответствующее заданным степеням свободы и уровню значимости.

4. Открыть окно "Ответы", ввести рассчитанные значения и проверить результаты. Если проверка указала на ошибку, тогда необходимо повторить расчет, вновь ввести и проверить результат.

Отчет по работе должен содержать:

• название и цель работы;

• исходные данные;

• последовательность выполнения работы;

• результаты вычислений и выводы по ним.

Лабораторная работа N1

Определение оценок статистических характеристик случайной

величины по выборке

Цель работы:

получить навыки в вычислении оценок параметров нормального закона распределения по выборке экспериментальных данных; проверке гипотезы о равенстве математического ожидания и дисперсий.

Методика выполнения

1. Запустить в директории STAT программу LW1, получить исходные данные для расчета – две выборки значений: случайные величины объемом n₁ и n₂ соответственно. Примером такой случайной величины может служить температура воздуха, зафиксированная в различных районах города с помощью какого-либо измерительного прибора. Выборки содержат результаты измерений в первый и второй дни.

2. Используя формулы несмещенных оценок, вычислить математическое ожидание (), дисперсию () и среднеквадратичное отклонение () для каждой выборки.

3. Задавшись уровнем значимости q = 0,05 и соответствующими значениями степеней свободы (v=n-1), найти по статистическим таблицам значения квантилей распределения статистик Стьюдента () и Xи-квадрат для каждой выборки.

4. Вычислить минимальную и максимальную границы доверительных интервалов на математическое ожидание выборок:

5. Вычислить минимальную и максимальную границы доверительных интервалов на дисперсию выборок.

6. Используя критерий Стьюдента, проверить гипотезу о равенстве математических ожиданий случайной величины в двух выборках

7. Используя критерий Фишера, проверить гипотезу о равенстве дисперсий случайной величины в двух выборках .

8. Оформить отчет по выполненной работе и сделать соответствующие заключения.

Контрольные вопросы

1. Что такое генеральная совокупность?

2. Какие характеристики можно оценить по выборке значений случайной величины?

3. Какую информацию можно получить, вычислив доверительный интервал на математическое ожидание и дисперсию?

4. Какие можно сформулировать гипотезы о математическом ожидании, найденном по выборочным значениям? Приведите пример.

5. Какие выводы можно сделать на основании полученных результатов обработки?

6. Придумайте ситуацию, в которой значения случайной величины могут быть представлены несколькими выборками.

Лабораторная работа N2

Экспериментальный анализ одномерной случайной величины

Цель работы:

изучить методику статистического определения закона распределения случайной величины по конечной выборке.

Методика выполнения

1. Запустить в директории STAT программу LW2, получить исходные данные для расчета – выборку значений случайной величины объемом n. Примером такой случайной величины может быть – объем продаж какого-либо товара. Необходимо провести статистический анализ этих экспериментальных данных.

2. По исходной выборке определить максимальное x_min и минимальное x_max значения случайной величины. Определить количество интервалов:

k=1+3.32 lg n

и построить ось, разбитую на интервалы

.

3. Построить гистограмму, для чего необходимо подсчитать число попаданий случайной величины в каждый i-й интервал, указанный на оси, определить относительную частоту

4. Выбрать закон распределения, для которого будет проводиться проверка гипотезы принадлежности данной выборки этому закону распределения (например, нормальный закон распределения).

5. Для каждого i-го интервала определить значения теоретической вероятности f_i . Для нормального распределения можно использовать таблицы функции Лапласа, предварительно преобразовав границы интервалов случайной величины х следующим образом .

6. Вычислить расчетное значение критерия Пирсона, используя частоты попадания случайной величины в соответствующий интервал:

 = n.

7. Определить по статистическим таблицам критические значения критерия для соответствующих степеней свободы () и уровня значимостиq = 0,05 (– односторонняя область) илиq = 0,025 (– двухсторонняя область).

8. Сравнивая расчетное и критическое значения критерия, решить вопрос о принятии или отклонении гипотезы о принадлежности генеральной совокупности к заданному закону распределения

.

8. Оформить отчет по выполненной работе и сделать соответствующие заключения.

Контрольные вопросы

1. Какие законы распределения случайной величины вы знаете?

2. Какими параметрами можно охарактеризовать каждый закон распределения?

3. Как определяется число интервалов для построения гистограммы?

4. В каком случае принимается гипотеза о принадлежности выборки к заданному закону распределения?

5.Как определяется теоретическое значение вероятности попадания в каждый интервал?

Лабораторная работа N 3

Изучение методов описательной cтатистики на примере ППП STATISTICA

Цели работы:

получить навыки расчета основных статистических характеристик случайных величин: математического ожидания, дисперсии, СКО и др. – по конечной выборке наблюдений, изучить методику построения гистограммы и определения закона распределения вероятности случайной величины по конечной выборке наблюдений.

Пример 1. Вычисление основных статистических характеристик.

Рассмотрим методику выполнения расчетов. Требуется определить среднюю величину дневной выручки в магазине. Пусть вы располагаете выборкой этой величины, которая фиксировалась кассиром ежедневно в течение месяца. Эти данные приведены в табл.1.

Для решения поставленной задачи необходимо по данным этой выборки определить оценки математического ожидания случайной величины (выручки), дисперсии и среднеквадратичного отклонения. Затем построить доверительный интервал оценки математического ожидания, задавшись приемлемой доверительной вероятностью (например, 95%).

Таблица 1.Исходные данные

День	Выручка (руб)	День	Выручка (руб)	День	Выручка (руб)
1	27479,27	11	38077,50	21	53686,90
2	39469,80	12	69720,76	22	69582,56
3	43501,55	13	38106,10	23	30865,84
4	39264,79	14	50553,20	24	44048,56
5	30043,48	15	43583,21	25	61449,22
6	67662,00	16	41282,52	26	53349,40
7	68987,42	17	46200,47	27	55048,30
8	35961,27	18	45346,07	28	39927,48
9	36232,53	19	54307,78	29	38368,89
10	50277,72	20	67304,06	30	31470,00

Последовательность выполнения

1. Запустите программу STATISTICA 6.0 и в появившемся окне (рис.1) настройте окно с данными для решения своей задачи. Скорее всего, в этом окне будет пустая таблица или таблица с одним из ранее использовавшихся наборов данных. Можете закрыть эту таблицу, нажав кнопку х в правом верхнем углу файла данных.

Рис.1. Начальное окно системы STATISTICA

2. Теперь нужно создать свою электронную таблицу данных. В основном окне системы выберите меню Файл (рис.2) и команду Новый…. В диалоговом окне создания новых документов Create New Document (рис.3) выберите вкладку Крупноформатная таблица и укажите число переменных и число регистров (наблюдений). В нашем примере имеется всего одна переменная и 30 наблюдений. Нажмите кнопку OK.

Рис.2. Меню Файл	Рис.3. Окно создания нового документа

3. Двойным щелчком по ячейке с именем VAR1 вызовите окно переменной и задайте имя переменной нашего примера – ВЫРУЧКА (рис.4), нажмите кнопку ОК.

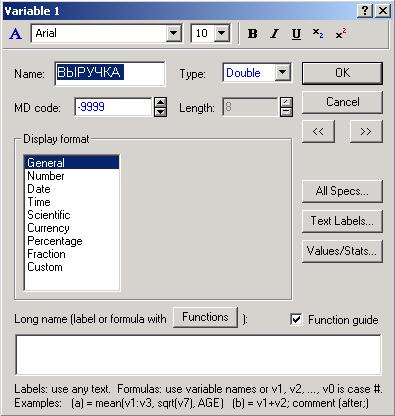
Рис.4. Задание формата для ввода переменной

4. В окне Данные (Data) введите значения выручки в магазине из табл.1. Сохраните файл с данными, выбрав свой каталог и введя имя файла (рис.5). По умолчанию файлам, содержащим таблицы данных, присваивается расширение .sta. В результате будем иметь файл данных (рис. 6).

Рис.5. Окно сохранения данных

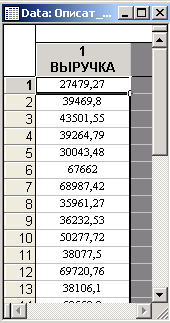
Рис.6. Окно с данными

5. Изучите режимы добавления и удаления переменных Vars и наблюдений Case, которые располагаются в панели форматирования. Добавьте новую переменную, выбрав команду Vars/Добавить и кажите число переменных (How many) – 1, нажмите кнопку ОК. В окне данных появится новая переменная NewVar. Щелкните мышкой по имени переменной NewVar и выберите команду Vars/Удалить. В результате файл данных будет содержать вновь одну переменную ВЫРУЧКА. Аналогично изучите добавления Case/Add и удаления Case/Delete наблюдений.

6. Теперь можно приступить к расчету требуемых статистических характеристик. С помощью команды меню Статистика / Основная статистика/Таблицы (рис.7) вызовите диалоговое окно основных статистик Basic Statistics and Tables (рис.8), выберите команду Descriptive statistics и нажмите кнопку ОК.

Рис.7. Меню команды Статистика	Рис. 8. Окно выбора метода основных статистик

7. В появившемся окне (рис.9), нажав кнопку переменные Variables, укажите имя исследуемой переменной (в данном случае она единственная в списке ВЫРУЧКА) (рис.10).

Рис. 9. Окно выбора метода основных статистик

Рис. 10. Окно задания переменной

8. Нажав кнопку ОК, вернитесь в окноDescriptive statistics и выберите вкладкуAdvanced. В появившемся списке укажите следующие статистические характеристики (рис.11):

þ математическое ожидание (Mean);

þ стандартное отклонение (Standard Deviation);

þ дисперсия (Variance);

þ доверительный интервал математического ожидания при доверительной вероятности 95% (conf. limits for means Interval 95%).

Рис.11. Окно задания рассчитываемых статистик

9. Запустите вычислительную процедуру, нажав кнопку Summary. На экране появится таблица результатов (рис.12). Результаты расчета основных характеристик случайной величины показывают, что величина ежедневной выручки в магазине с вероятностью 95% лежит в пределах от 42304,96 до 51772,28 руб. и в среднем составляет 47038,62 руб.

Рис.12. Результат расчета основных характеристик случайной величины

10. Визуальную интерпретацию результатов можно представить с помощью двумерного графика. Для этого вновь активизируйте диалоговое окно Descriptive statistics, свернутое в нижней части экрана, нажав на него мышкой. Выберите во вкладке Quick режим Box & Whisker Plot for alls variables. В окне результатов появится новая вкладка с графиками (рис.13), где отображаются среднее значение, стандартная ошибка, стандартное отклонение.

Рис.13. Диаграмма размаха значений случайной величины

Смысл этого графика очень простой: точка в центре прямоугольника (ящика) соответствует среднему значению выручки. От этого значения откладывается положительная и отрицательная величина стандартной ошибки (ширина ящика) и положительная и отрицательная величина стандартного отклонения (усы).

Программа позволяет хранить не только исходные данные, но и результаты расчета. Для этого при открытом окне результатов вызвать команду Файл/Сохранить (или Сохранить как), задать имя файла результатов и место его хранения. В результате получим файл с расширением .stw.

Пример 2. Экспериментальный анализ одномерной случайной

величины.

Во многих случаях перед тем, как проводить основной анализ данных, требуется установить, к какому из известных законов распределения вероятности принадлежит наблюдаемая величина. Исследуем прибыль от реализации товара на предприятии как непрерывную случайную величину, распределенную предположительно по нормальному закону. Исходные данные о прибыли, полученные при ее ежедневной регистрации в течение 100 дней (объем выборки n=100), приведены в табл.2.

Таблица 2. Исходные данные о прибыли

47,00	54,67	56,94	44,87	66,61	54,54	54,44
37,22	58,75	53,23	69,72	33,88	49,74	56,18
52,44	55,96	40,60	58,66	55,39	39,45	52,13
62,76	36,28	47,59	73,76	59,02	32,25	39,73
61,98	38,84	51,32	43,45	69,19	58,28	62,38
67,33	43,10	55,58	50,72	49,15	35,56	46,89
28,16	33,10	51,39	58,30	44,76	41,53	41,60
47,66	31,53	40,89	58,62	56,75	34,78	41,79
60,95	40,22	68,85	43,63	46,19	46,37	45,71
39,13	42,26	54,87	40,77	57,58	49,68	45,47
24,22	28,82	46,73	61,11	72,06	50,28
64,48	44,32	46,30	37,99	64,44	46,77
37,20	45,96	63,43	34,41	63,04	71,95
43,46	51,35	49,15	57,11	51,13	32,58
57,58	46,35	48,14	56,38	50,02	42,64