Elektrichestvo_i_Magnetizm_18lr_sec

Построить график зависимости натурального логарифма lnIдрейф от

1/T (табл.2).

Построить на нём прямую наилучшего соответствия. Определить её угловой коэффициент b, который должен быть равен из (5)

b = qUk к ,

(6)

где k = 1,38 10–23 Дж/K, q = 1,6 10–19 Кл.

Определить контактную разность потенциалов Uк из (6).

5. Сравнить Uк, полученную тремя разными способами со справочным значением Uк=0,35±0,05 В и сделать выводы.

131

Работа № 17. ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА С ПОМОЩЬЮ ДАТЧИКА ХОЛЛА

ЦЕЛЬ: экспериментально исследовать магнитное поле на оси короткого и длинного соленоида и сравнить его с расчетным.

ОБОРУДОВАНИЕ: регулируемый источник постоянного напряжения, миниблок «Соленоиды», миниблок «Ключ», два мультиметра, линейка.

В в е д е н и е

Любой проводник с током создает вокруг себя магнитное поле, величина и конфигурация которого зависит от тока, протекающего по проводнику, и формы проводника. В общем случае значение вектора индукции маг-

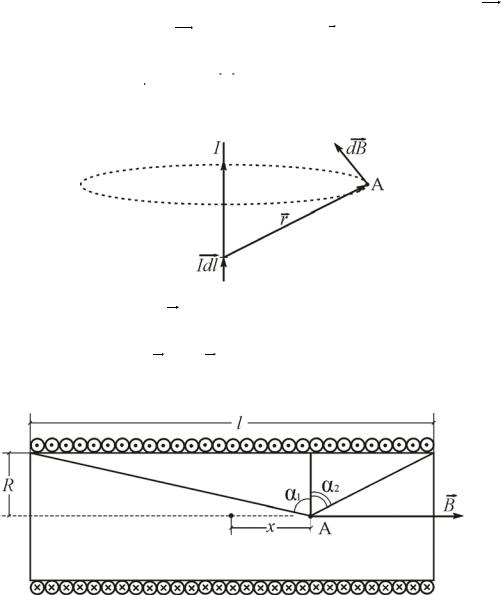
нитного поля описывается законом Био- Савара-Лапласа. Элемент тока Idl

Рис. 1

Полное значение вектора В, созданного проводником конкретной формы вычисляется с использованием принципа суперпозиции

Рис. 2

132

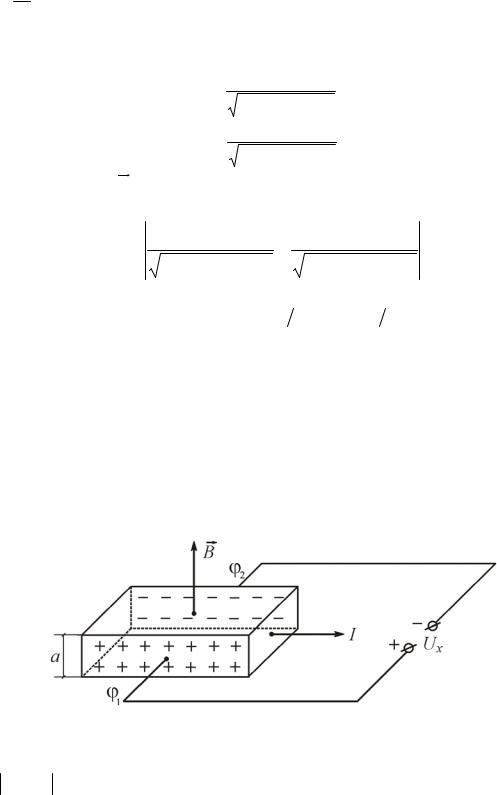
Например в точке А (рис. 2) на оси соленоида (с однослойной намоткой) вектор индукции магнитного поля:

где n = Nl - число витков на единицу длины соленоида,

α1,α2 - углы, под которыми из точки А видны концы соленоида.

Если известно расстояние точки А от середины соленоида «х», то

Т.о. модуль вектора В на оси соленоида в точке, отстоящей на расстоянии х от его середины равен

и магнитное поле является практически однородным.

Если соленоид короткий (l ≈ R), то магнитное поле его резко неоднородно и рассчитывается по формуле (4).

М е т о д и з м е р е н и й

В данной работе измерение вектора индукции магнитного поля основано на применении датчика Холла.

Рис.3

Явление Холла заключается в возникновении разности потенциалов (Ux = ϕ1 −ϕ2 ) при протекании постоянного тока I через проводящую пла-

133

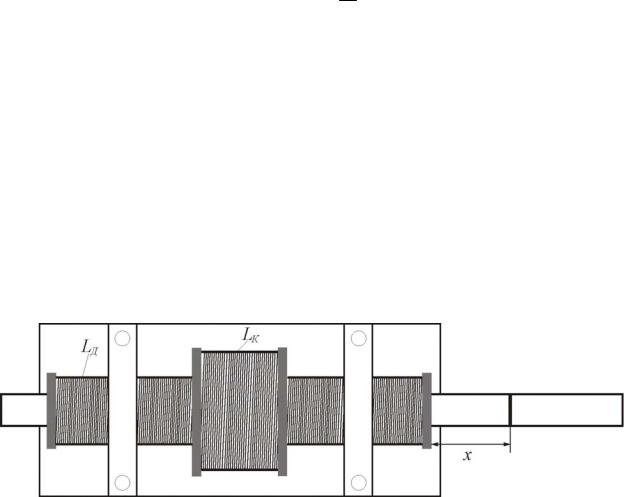
стину толщиной а, помещенную в магнитное поле, перпендикулярное направлению тока (рис. 3):

U x = Rx IBa ,

где Rx - постоянная Холла, зависящая от свойств пластины.

Эта разность потенциалов пропорциональна величине индукции магнитного поля В в той точке пространства, куда помещен датчик.

Т.к. датчик имеет малые размеры (~ мм), то с его помощью можно исследовать магнитное поле.

Для перевода показаний датчика Холла Ux в значение вектора магнитной индукции B(Тл) достаточно знать градуировочный коэффициент γ данного датчика.

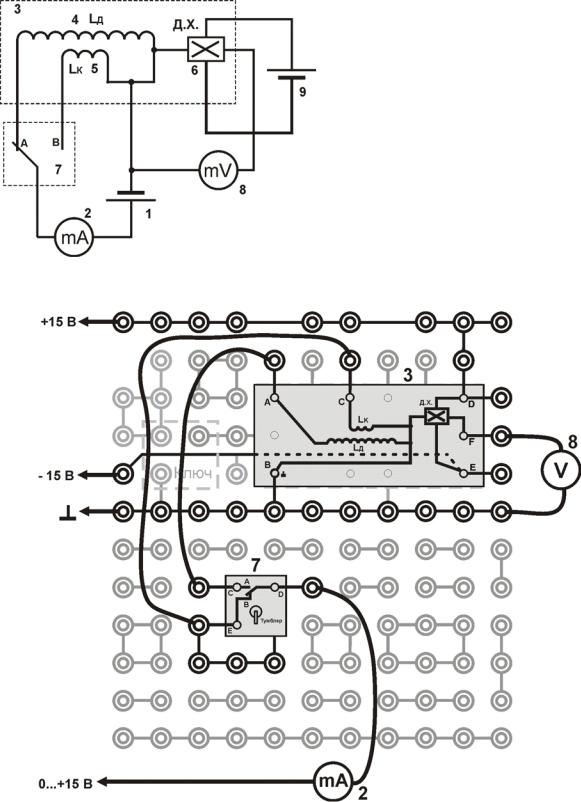
Рис. 4 Установка (миниблок «Соленоиды») состоит из двух соленоидов

(рис.4), закрепленных на панели. Короткий соленоид LК закреплен снаружи длинного соленоида LЦ . Середины соленоидов совпадают, совпадают и

оси соленоидов. Вдоль оси соленоидов может перемещаться шток. Внутри штока помещен датчик Холла (Д.Х.). Расстояние датчика от середины соленоида х совпадает с расстоянием риски на штоке от конца катушки цилиндрического соленоида.

Электрическая схема установки приведена на рис. 5.

Питание соленоидов осуществляется от регулируемого источника постоянного напряжения «0…+15 В» 1. Ток в соленоидах измеряется миллиамперметром 2. Переключатель 7 позволяет подключать к источнику напряжения 1 либо длинный соленоид 4 (положение переключателя А) либо короткий 5 (положение переключателя В). Измерение индукции магнитного поля соленоида осуществляется с помощью датчика Холла (Д.Х.) 6. Измерение холловой разности потенциалов U x осуществляется с помо-

134

щью вольтметра 8. Питание датчика Холла осуществляется от источника стабилизированногопостоянногонапряжения«±15 В» 9.

Рис. 5 Электрическая схема:

1 – регулируемыйисточникпостоянногонапряжения«0…+15 В»; 2 – мультиметр (режим A 200 mA, входы COM, mA); 3 – миниблок «Соленоиды»; 4 – длинныйсоленоидсиндуктивностью LД ; 5 – корот-

кийсоленоидсиндуктивностью LК ;

6 – датчикХолла; 7 – миниблок «Ключ»; 8 – мультиметр (режим

V 2 mВ, входы COM, VΩ); 9 – ис-

точникстабилизированногопостоянногонапряжения«±15 В»

Рис. 6. Монтажная схема установки: 2, 3, 7, 8 – см. на рис. 5

135

П о р я д о к в ы п о л н е н и я р а б о т ы

Выполнение измерений

7.Соберите электрическую цепь по монтажной схеме, приведенной на рис. 6. Установите необходимые режимы измерения мультиметров

2 и 8 (см рис. 5).

8.Включите кнопками «Сеть» питание блока генераторов напряжения и блока мультиметров. Нажмите кнопку «Исходная установка» (поз. 19, см. рис. 1 на стр. 6).

Задание 1. Градуировка датчика Холла.

1.С помощью тумблера на миниблоке «Ключ» подключите питание к длинному соленоиду (положение А).

2.Перемещая шток с датчиком Холла вдоль оси соленоида, установите его в середине соленоида (риски на штоке должна совпадать с концами цилиндрического соленоида).

Втаблицу 1 запишите параметры соленоида (оммическое сопротивление обмотки R, длина l, число витков N).

3.Кнопками установки напряжения «0…15 В» (поз.14, рис. 1, стр. 6) установите нулевой ток в соленоиде (I=0 мА) и запишите в таблицу 1 напряжение на датчике Холла U0 (показания вольтметра 8).

Значение U0 обусловлено магнитным полем Земли и несимметричным расположением датчика.

4.Изменяя ток в соленоиде от 0 до 200 мА ( с интервалом 20мА) зафиксируйте напряжение на датчике Холла U и результаты занесите

втаблицу 1.

5.Рассчитайте магнитное поле, созданное только током в соленоиде. Для этого из показаний датчика Холла U необходимо вычесть U0 . Значение U −U0 запишите в таблицу 1.

6.По формуле (5) для каждого значения тока рассчитайте и запишите

втаблицу значения вектора магнитной индукции B .

136

Задание 2. Исследование магнитного поля на оси цилиндрического соленоида.

1.С помощью тумблера на миниблоке «Ключ» подключите питание к длинному соленоиду (положение А) и установите датчик Холла в середину соленоида ( x = 0). В таблицу 2 запишите параметры соленоида.

2.Кнопками установки напряжения «0…15 В» (поз.14, рис. 1, стр. 6) установите нулевой ток в соленоиде (I=0 мА) и запишите в таблицу

1напряжение на датчике Холла U0 .

3.Кнопками установки напряжения «0…15 В» (поз.14, рис. 1, стр. 6) установите (по указанию преподавателя) ток I в соленоиде и его значение запишите в таблицу 2.

В течении всей работы ток I должен оставаться строго постоянным!

4.Перемещая шток с датчиком Холла вдоль оси соленоида (с шагом 1 см), зафиксируйте напряжение на датчике Холла U(мВ) и результаты

занесите в таблицу 2.

Помните! x = 0 соответствует положению датчика Холла в середине соленоида.

Примечание. Так как соленоид симметричный достаточно провести измерения, перемещая датчик в одну сторону. Для сомневающихся предлагается перемещать датчик в обе стороны.

5.Рассчитайте U −U0 (поле, созданное только током) для каждого положения датчика и результаты занесите в таблицу 2.

137

6.Рассчитайте индукцию магнитного поля соленоида BЭ по формуле (6), используя градуировочный коэффициент <γ > (см упр.1). Результаты занесите в таблицу 2.

7.Для соответствующих значений x (положений датчика Холла) проведите теоретический расчет индукции магнитного поля BТ по формуле (4). Результаты занесите в таблицу 2.

8.Постройте графики зависимости BЭ и BТ от положения датчика Холла x: BЭ = f (x) и BТ = f (x) . Сравните их и сделайте выводы.

Задание 3. Исследование магнитного поля на оси короткого соленоида.

1.С помощью тумблера на миниблоке «Ключ» подключите питание к короткому соленоиду (положение В).

2.Повторите пункты 2 – 8 упражнения 2, но при шаге перемещения датчика – 2 мм.

3.Выключите кнопками «Сеть» питание блока генераторов напряжения и блока мультиметров.

К о н т р о л ь н ы е в о п р о с ы

1.Что такое вектор индукции магнитного поля?

2.Сформулируйте закон Био-Савара-Лапласа.

3.В чем заключается принцип суперпозиции?

4.Как можно рассчитать магнитное поле соленоида?

5.Как можно получить однородное магнитное поле?

6.В чем отличие магнитных полей короткого и длинного соленоида?

7.В чем заключается явление Холла?

8.Как устроен датчик Холла и как с его помощью можно исследовать магнитное поле?

9.Физический смысл градуировочного коэффициента датчика Холла?

10.Как можно экспериментально определить градуировочный коэффициент для датчика Холла?

11.Как при измерении магнитного поля соленоидаможно исключить влияние магнитного поля Земли и несимметричность расположения датчика?

Л и т е р а т у р а

5.Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989. –

§§16.2, 16.3.

6.Калашников С.Г. Электричество. – М.: Наука, 1977. – §§ 31, 32.

138

Работа № 18. ВЗАИМНАЯ ИНДУКЦИЯ ДВУХ СОЛЕНОИДОВ

ЦЕЛЬ: экспериментально определить коэффициент взаимной индукции двух соленоидов и сравнить результат с рассчитанным теоретически.

ОБОРУДОВАНИЕ: генератор сигналов специальной формы, миниблок «Соленоиды», два мультиметра.

В в е д е н и е

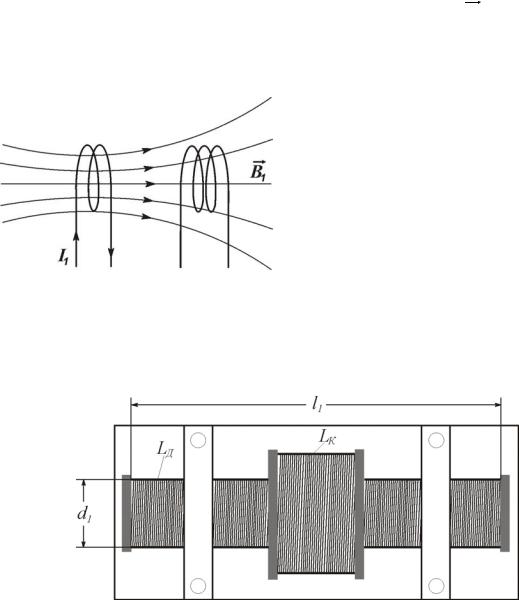
Контурстоком I1 создаетвокругсебямагнитноеполе В1 . Есливблизи

этогоконтурапоместитьдругойконтур, тоснимокажетсясцепленнекоторый магнитныйпоток Ф2 (рис. 1). Этот магнитный поток, как показывает опыт и

теория, пропорционален величине тока в первом контуре (рис. 1)

Ф2 = М21I1 .

Коэффициент пропорциональности М21 между магнитным потоком Ф2 ,

сцепленным со вторым контуром и током I1 , текущимпопервомуконтуру,

называетсякоэффициентомвзаимной индукциивторогоконтураспервым.

Рис. 1

Исследуемкоэффициентвзаимнойиндукцииконтуровнапримередвух соленоидов, осикоторыхсовпадаютиодинизних(короткий) LК помещен

снаружидлинного LД вегосередине(рис. 2).

Рис. 2

Длинныйсоленоид(l1 >> d1 ) создает в средней его части (где распо-

ложен короткий) практически однородное магнитное поле (см работу №16), вектор индукции которого равен

139

где N1 - число витков длинного соленоида, l1 - его длина.

Магнитный поток через сечение S1 = πd412 длинного (а следовательно и через сечение короткого) равен

Так как магнитное поле снаружи длинного соленоида отсутствует, то магнитный поток сцепленный с коротким соленоидом

Ф2 =Ф1N 2= µµ0 N1 S1I1N2 , (3)

l1

где N2 - число витков короткого соленоида.

Следовательно коэффициент взаимной индукции второго с первым соленоидом

Если через длинный соленоид пропустить переменный ток

(где ω = 2πν - циклическая частота тока), то магнитный поток сцепленный с коротким соленоидом будет переменным

где I 0 - амплитуда переменного тока в длинном соленоиде.

Электроизмерительные приборы (в том числе и мультиметры) измеряют действующие значения тока и напряжения

140