
Elektrichestvo_i_Magnetizm_18lr_sec
.pdf
5.Подсоедините параллельно к конденсатору С1 второй конденсатор С2 и повторите аналогичные измерения для параллельно-соединенных конденсаторов Спарал .
6.Выключите кнопками «Сеть» питание блока генераторов напряжения и блока мультиметров.
Таблица
t, c |
С1 = … |
мкФ |
Спарал = … |
мкФ |
|
U1, B |
ln U1 |
Uпарал , B |
ln Uпарал |
||
|
|||||
0 |
|
|
|
|
|
5 |
|
|
|
|
|
10 |
|
|
|
|
|
15 |
|
|
|
|
|
20 |
|
|
|
|
|
25 |
|
|
|
|
|
30 |
|
|
|
|
|
35 |
|
|
|
|
|
40 |
|
|
|
|
|
45 |
|
|
|
|
|
50 |
|
|
|
|
|
55 |
|
|
|
|
Средняя точка (Приложение 1.1)
Обработка результатов измерений
1. Рассчитайте и запишите в таблицу емкость конденсатора Спарал по форму-
ле для параллельного соединения:
Спарал =С1 +С2 =…мкФ
2.На одном поле чертежа постройте графики зависимостей U1= f(t) и ln U1= f(t) для конденсатора С1 , а на другом Uпарал = f(t) и ln Uпарал = f(t) для кондерасатора Спарал , располагая ось напряжения U с левой стороны, а ось ln U
– с правой.
3.Определите по графикам ln U1= f(t) и ln Uпарал = f(t) угловые коэффициенты К1 и Кпарал линейных зависимостей (см. приложение 1 формула (1)) и
постоянные времени цепи τ |
|
= − |
1 |
и τ |
|
= − |
1 |
для каждого значения |
1 |
|
парал |
|
|||||
|
|
К1 |
|
Кпарал |
||||
емкости.
4.Рассчитайте сопротивление вольтметра R по формуле (5) для каждого значения емкости:
111

R |
= τ1 |
= … Ом, R |
= |
τпарал |
= … Ом |
|
|||||
1 |
C1 |
парал |
|
Cпарал |
|
|
|
|
|||
5. Оцените относительную погрешность измеренных величин:
δR |
= δС2 +δ |
К2 δ |
К |
1 |
и δR |
= δС2 |
+δК2 |
δК |
, |
1 |
1 |
1 |
|
парал |
парал |
парал |
|
парал |
где δК1 и δКпарал – погрешности угловых коэффициентов (см. формулу (4) в приложении1).
6.В выводе по работе сделайте анализ полученных экспериментальных зависимостей и оцените точность метода определения постоянной времени.
К о н т р о л ь н ы е в о п р о с ы
1.Какой ток называют квазистационарным? Сформулируйте условие квазистационарности электрического тока.
2.Какие физические законы и формулы используются для получения зависимости напряжения от времени при разряде конденсатора?
3.По какому закону изменяются со временем при разряде конденсатора следующие величины: 1) заряд обкладки, 2) напряжение конденсатора, 3) ток в RC-цепи?
4.Какую величину называют постоянной времени цепи и что она показывает?
5.Как связана постоянная времени RC-цепи с параметрами этой цепи?
6.Укажите режим работы мультиметра при проведении измерений: измеряемая величина, режим и входы для подключения прибора.
7.Какое назначение имеет источник питания в исследуемой электрической цепи?
8.С какой целью в работе строят график зависимости ln U=f(t)?
9.Каким образом можно показать, что опытная зависимость является экспоненциальной? \
10.Как экспериментально определяют постоянную времени цепи, содержащей R и C?
11.Каким способом в данной работе измеряют сопротивление вольтметра? 12.Какие формулы используют в работе для определения следующих величин:
а) постоянной времени цепи, б) сопротивления мультиметра?
13.Как оценивают в работе погрешность определения постоянной времени?
Л и т е р а т у р а
1.Детлаф А.А., Яворский Б.М. Курс физики. –М.: Высшая школа, 1989. –
§§19.1, 27.3.
2.Калашников С.Г. Электричество. –М.: Наука, 1975. – §§ 73, 74.
112
Работа № 15. ИЗУЧЕНИЕ СВОЙСТВ СЕГНЕТОЭЛЕКТРИКА |
|||||
ЦЕЛЬ: по предельной петле гистерезиса ознакомиться с методом измере- |
|||||
ния основных характеристик сегнетоэлектриков, исследовать зави- |
|||||
симость диэлектрической проницаемости сегнетоэлектрика от на- |
|||||
пряженности электрического поля. |
|
||||
ОБОРУДОВАНИЕ: генератор сигналов специальной формы, миниблок |
|||||
|
«Сегнетоэлектрик», осциллограф, два мультиметра. |
||||
|
|
|
В в е д е н и е |
|
|
Сегнетоэлектрики – группа кристаллических диэлектриков, у кото- |
|||||
рых в некотором интервале температур в отсутствии внешнего элек- |
|||||
трического поля отсутствует спонтанная (самопроизвольная) поляризо- |
|||||
ванность PS |
( PS - электрический дипольный момент единицы объема ве- |
||||
щества вне электрического поля). Величина и направление вектора PS |
|||||
существенно зависят от электрического поля, механических напряжений, |
|||||
измерения температуры и др. Впервые сегнетоэлектрические свойства |
|||||
были подробно исследованы И.В. Курчатовым и П.П. Кобеко у сегнетовой |
|||||
соли (натрий-каливая соль винной кислоты) NaKC4H4 4H2O, откуда и воз- |
|||||
никло название этого класса диэлектриков. Примерами сегнетоэлектриков |
|||||
являются |
титанат |
бария |
ВаТiO3, |
триглицинсульфат |
|
(NH2CH2COOH)3 3H2SO4 и др. |
|
|
|||
Сегнетоэлектрики имеют важное практическое применение. Напри- |
|||||
мер, приготовляя сложные диэлектрики на основе сегнетоэлектриков и до- |
|||||
бавляя к ним различные примеси, можно получить высококачественные |
|||||
конденсаторы большой ёмкости при их малых размерах. |
|||||
|
|
|
Сегнетоэлектриками |
могут быть только |
|
|
|
|
кристаллические тела, у которых решетка не |
||
|
|
|
имеет центра симметрии. Например, кристал- |
||
|
|
|
лическая решетка титаната бария состоит как |
||
|
|
|
бы из трех встроенных друг в друга кубиче- |
||
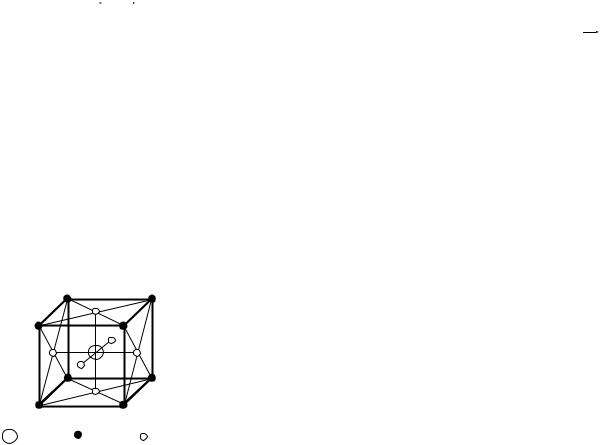
|
– Ва2+, – O2– |
ских подрешеток: одна образована положи- |
|||
– Ti4+, |
тельными ионами бария, другая – отрицатель- |
||||
Рис. 1 |
|
ными ионами титана, третья – отрицательны- |
|||
|
|
|
ми ионами кислорода (рис. 1). Минимум энер- |
||
гии взаимодействия между положительными ионами титана и отрицатель- |
|||||
ными ионами кислорода достигается, если они смещаются навстречу друг |
|||||
другу, нарушая тем самым симметрию элементарной кристаллической |
|||||
ячейки. Если такое смещение происходит во всех элементарных ячейках |
|||||
кристалла, то сегнетоэлектрик приобретает очень большой электрический |
|||||
дипольный момент в направлении этого смещения. В результате сильного |
|||||
электрического взаимодействия между |
отдельными поляризованными |
||||
|
|
|
|
|
113 |
ячейками они располагаются так, что их дипольные моменты параллельны друг другу. Такое расположение дипольных моментов возможно даже в отсутствие внешнего электрического поля. Это и есть спонтанная поляри-
зованость PS .
Сегнетоэлектрики отличаются от остальных диэлектриков рядом особенностей:
1.Большое значение диэлектрической проницаемости ε (~ 105), в то время как у большинства обычных диэлектриков она составляет несколько единиц.
2.Нелинейная зависимость поляризованности от напряженности электрического поля Е.
Это приводит к тому, что диэлектрическая проницаемость сегнетоэлектрика зависит от напряженности поля. Для обычных диэлектриков эта величина не зависит от поля и является характеристикой вещества.
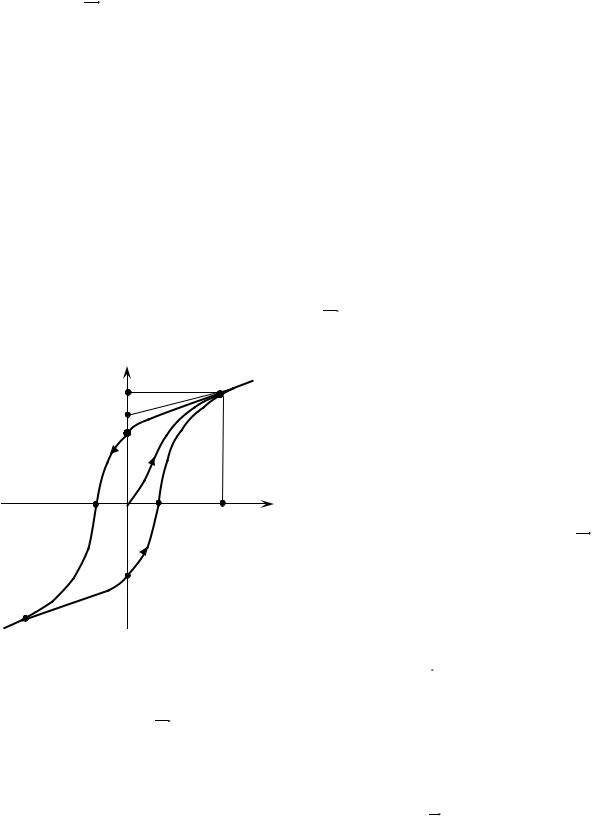
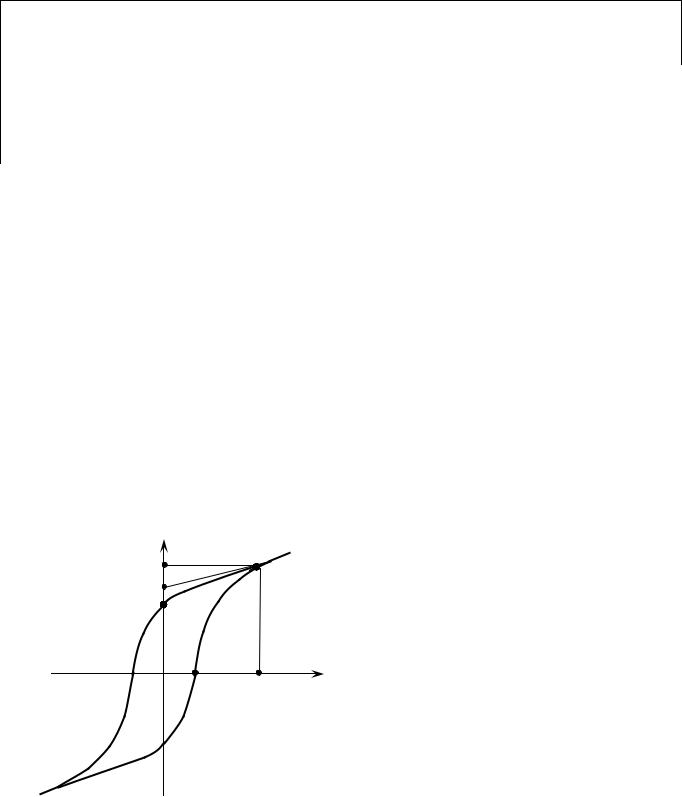
3.Обладают диэлектрическим гистерезисом («запаздывание»). Рассмотрим поведение сегнетоэлектрика при циклическом изменении внешнего электрического поля (рис. 2). При Е = 0 в сегнетоэлектрике существу-
ет только спонтанная поляризованность PS . Если макроскопический объём
|
Р |
|
|
* |
сегнетоэлектрика спонтанно поляри- |
||||
|
1 |
1 |
зован, |
то он |
является |
источником |
|||
|
Рнас |
|
сильного электрического поля. С |
||||||
|
|
|
|
||||||
|
РS |
|
|
|
этим полем связана большая энергия. |
||||
|
Рос |
2 |
|
|
Следовательно, такое состояние яв- |
||||
|
|
|
|
|
ляется |
энергетически |
невыгодным. |
||
|
3 О |
6 |
Е |
Система из такого состояния стре- |
|||||
|
мится перейти к состоянию с мень- |
||||||||
|
–Ек |
+Eк Енас |
|
|
шей энергией, сохраняя при этом |
||||
|
|
|
|
|
спонтанную поляризованность PS . |
||||
|
|
5 |
|
|
Это осуществляется путем разделе- |
||||
|
* 4 |
|
|
ния макроскопического объёма сег- |
|||||
4 |
|
|
|
нето-электрика |
на |
малые области – |
|||
Рис. 2 |
|
|
домены, каждый из которых характе- |
||||||
|
|
|
|||||||
|
|
|
ризуется вектором спонтанной поля- |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
ризованности |
PS |
(рис. |
3). Размеры |
|
доменов порядка десятков тысяч ангстрем (порядка микрометра) В пределах одного домена PS всех элементарных ячеек ориентирован в одну сто-
рону, но в разных доменах он ориентирован произвольно, поэтому средняя поляризованность всего сегнетоэлектрика равна нулю (точка 0 на рис. 2 и рис. 3а).
При наложении внешнего электрического поля Е поляризованность сегнетоэлектрика изменяется. Она будет складываться из спонтанной по-
114
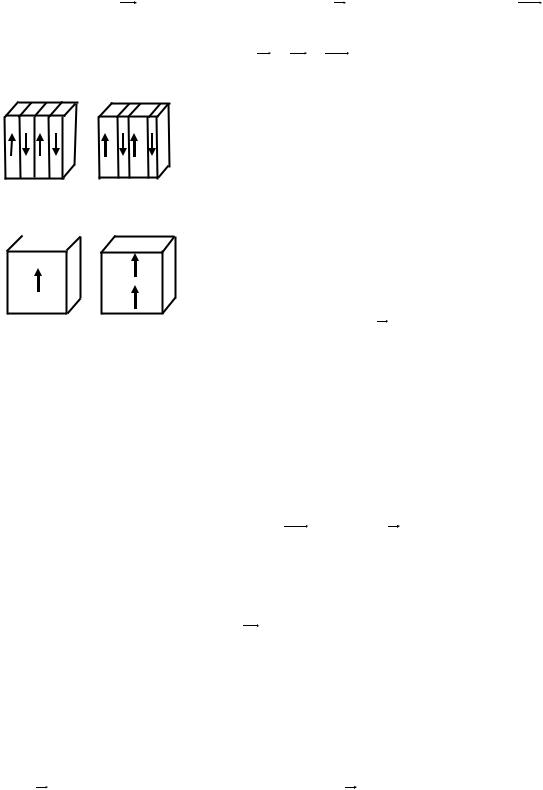
ляризованности PC , не зависящей от поля Е, и индуцированной Pинд , вызванной этим полем,
|
|
|
P = PC + Pинд . |
|
|
|
Первоначальное увеличение поляризован- |
|
|
|
ности происходит из-за роста доменов, с |
|
|
|
«выгодной» ориентацией за счет доменов с |
|
|
|
«менее выгодной» ориентацией (рис. 3б). |
|
|
|
«Выгодной» считается такая ориентация |
а) Е= 0 б) 0 < Е < Eнас |
дипольных моментов, которая образует |
||
|
|
|
острый угол с направлением внешнего |
|
|
|
электрического поля. Наиболее интенсивно |
|
|
|
|
|
|
|
этот процесс протекает для среднего участ- |
|
|
|
ка кривой 0-1. В точке 1 поляризованность |
|
|
|
всех доменов оказывается ориентирован- |
с) Е = Eнас |
д) Е > Eнас |
ной вдоль поля Е и сегнетоэлектрик пре- |
|
|
Рис. 3 |
вращается в однодоменный кристалл (рис. |
|
|
3с). Он находится в состоянии насыщения |
||
|
|
|
и характеризуется напряженностью ЕНАС и |
поляризованностью РНАС насыщения. Дальнейшее увеличение Е приводит
к незначительному возрастанию поляризованности и кривая 0-1 переходит в линейный участок 1-1* (рис. 3д). Увеличение поляризованности на этом участке происходит за счет индуцированной поляризованности, которая линейно зависит от электрического поля Е
Pинд =ε0 (ε −1)Е, |
(1) |
где ε0 = 8,85 10–12 Ф/м – электрическая постоянная. Так как при достиже-
нии состояния насыщения поляризованность равна сумме спонтанной и индуцированной поляризованности, то для определения максимальной
спонтанной поляризованности PS необходимо экстраполировать прямую
1-1*. до пересечения с осью Р.
При уменьшении (из точки 1) поля кривая зависимости Р от Е не совпадет с первоначальной и пойдет несколько выше (кривая 1-2). При Е = 0 сегнетоэлектрик не возвращается в неполяризованное состояние, а сохраняет остаточную поляризованность Рост (отрезок 0-2). Это явление на-
зывается диэлектрическим гистерезисом. Таким образом, поляризован-
ность Р не определяется однозначно полем Е, а зависит также от предшествующей истории сегнетоэлектрика.
Для деполяризации сегнетоэлектрика т. е. сведения к нулю остаточной поляризованности, необходимо приложить некоторое поле ЕК обратного
направления. Напряженность ЕК (отрезок 0-3) называется коэрцитивной силой (коэрцитивным полем). При дальнейшем увеличении поля того же
115
направления поляризованность кристалла меняет свое направление и с ростом поля достигает насыщения в точке 4. Дальнейший рост (от точки 4 до 4*) обусловлен действием индуцированной поляризованности. Если вновь изменять напряженность от – ЕНАС до + ЕНАС , то электрическое состояние сегнетоэлектрика будет изменяться вдоль ветви 4*-4-5-6-1-1*. Значение остаточной поляризованности для этой ветви определяется отрезком 0-5, а коэрцитивной силы – отрезком 0-6. Замкнутая кривая 1*-1-2-3-4-4*-5- 6-1-1* называется петлей гистерезиса.
При изменении напряженности поля от – Е до + Е и последующем возвращении от + Е до – Е, где Е – любое значение напряженности поля, удовлетворяющее условию 0 < Е < ЕНАС , будет также получаться петля гистерезиса, называемая частной петлей (частным циклом). Этих циклов может быть бесчисленное множество, при этом вершины частных петель лежат на основной кривой 0-1.
М е т о д и з м е р е н и й
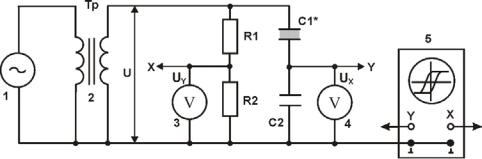
Изучить свойства сегнетоэлектриков и определить их основные харатеристики – поляризованность и напряженность поля при насыщении сегнетоэлектрика, остаточную поляризованность и коэффициентную силу можно с помощью петли диэлектрического гистерезиса. Получить и наблюдать петлю можно с помощью установки, электрическая схема которой приведена на рис. 4.
Два конденсатора С1 и С2 соединяются последовательно и питаются от регулируемого источника переменного напряжения. Конденсатор С2
заполнен обычным «линейным» диэлектриком с постоянной диэлектрической проницаемостью, а конденсатор С1 – сегнетоэлектриком. Параллель-
но соединению конденсаторов включены два сопротивленния. Сопротивление R1 является эквивалентным омическим сопротивлением исследуемо-
го сегнетоэлектрика, а сопротивление R2 . служит для подбора равенства фаз напряжений, подаваемых на вход осциллографа (ОЭ).
Рис. 4 Электрическая схема:
1 – генератор сигналов специальной формы (регулируемый источник постоянного напряжения); 2 – трансформатор; 3, 4 – мультиметры (режим
116

V 20 V, входы COM, VΩ); 5 – осциллограф; С1 – конденсатор с сегнетоэлектрическим изолятором; С2 – конденсатор с изолятором не из сегнетоэлектрика; X, Y – выходы напряжений U X и UY на мультиметры и на соответствующие гнезда осциллографа.
20 V, входы COM, VΩ); 5 – осциллограф; С1 – конденсатор с сегнетоэлектрическим изолятором; С2 – конденсатор с изолятором не из сегнетоэлектрика; X, Y – выходы напряжений U X и UY на мультиметры и на соответствующие гнезда осциллографа.
Ёмкость конденсатора С1 и напряженность электрического поля Е1
внутри сегнетоэлектрика рассчитываются по формулам |
|
|||||
С |
= |
|
ε0εs |
, |
(2) |
|
|
|
|||||
1 |
|
|
d |
|
||
|
|
|
|
|||
Е |
= |
UС1 |
, |
(3) |
||
|
||||||
1 |
|
|
d |
|
||
|
|
|
|
|||
где ε – диэлектрическая проницаемость, s – площадь обкладок, d |
– рас- |
|||||
стояние между ними, UС1 – напряжение между обкладками конденсатора
С1 .
Так как конденсаторы соединены между собой последовательно, то заряды на их обкладках будут одинаковыми
Q =C1UС1 =C2UС2 ,
где UС2 - на конденсаторе С2 . Отсюда
UС1 = C2 UС2 ,
C1
или учитывая (2)
U |
С1 |
= |
C2d U |
С2 |
. |
||||
|
|
ε εs |
|
|
|||||
Подставим (5) в (3), получим |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
||
Е |
=U |
|
|
. |
|||||
|
|
|
|||||||
|
1 |
|
|
C1 ε0εs |
|
||||
Из соотношения (1) с учетом того, что для сегнетоэлектрика ε ет
|
|
Е |
= |
Р |
. |
|
||
|
|
|
|
|
||||
|
|
|
1 |
|
ε |
ε |
|
|
Тогда уравнение (6) примет вид |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
Р |
|
=U |
|
C1 |
, |
||
|
ε0ε |
C1 ε0εs |
||||||
|
|
|
|
|||||
откуда следует, что
UС2 = s P , C2
(4)
(5)
(6)
>> 1, следу-
(7)
117
то есть, падение напряжения на конденсаторе С1 пропорционально поляри-
зованности сегнетоэлектрика.
Найдем падение напряжения UR 2 на сопротивлении R2 . Ток, текущий через это сопротивление по закону Ома равен
I = UR 2 .
R2
Такой же ток протекает и по участку цепи с сопротивлением (R1 + R2 )
I = UR1 |
+UR 2 |
, |
|
|||
|
|
R + R |
|
|
|
|
|
|
1 |
2 |
|
|
|
где UR1 – падение напряжения на сопротивлении R1 . Из сравнения двух |
||||||
последних уравнений получаем |
|
|
|
|
|
|
UR 2 |
= UR1 +UR 2 |
, |
||||
R |
2 |
R + R |
|
|
||
|
|
1 |
2 |
|
|
|
где UR1 +UR 2 =UC1 +UC 2 =U – напряжение, подаваемое на вход схемы (рис. 4).
Так как С2 >> С1 и R1 >> R2 , то из (4) следует, что UС1 >> UС2 |
и |
|||||
|
|
UR 2 = UC1 |
, |
|
||
|
|
R |
2 |
R |
|
|
|
|
|
1 |
|
|
|
откуда с учетом равенства (5), получаем уравнение |
|
|||||
U |
R 2 |
= R2d |
E , |
|
(8) |
|
|
R1 |
1 |
|
|
||
|
|
|
|
|
||
то есть, падение напряжения на сопротивлении R2 пропорционально на-
пряженности внешнего электрического поля.
Таким образом, из уравнений (7) и (8) видно, что если напряжение UС2 подать на вход вертикальной развертки осциллографа (UY ), а напряже-
ние UR 2 – на вход горизонтальной развертки (U X ), то электронный луч в
направлении оси Y будет отклоняться пропорционально поляризованности Р сегнетоэлектрика, а в направлении оси X – пропорционально напряжённости внешнего электрического поля Е. За один период синусоидального изменения напряжения электронный луч на экране опишет полную петлю гистерезиса, и за каждый последующий период в точности повторит её. Поэтому на экране будет наблюдаться неподвижная петля.
О п и с а н и е |
у с т а н о в к и |
118
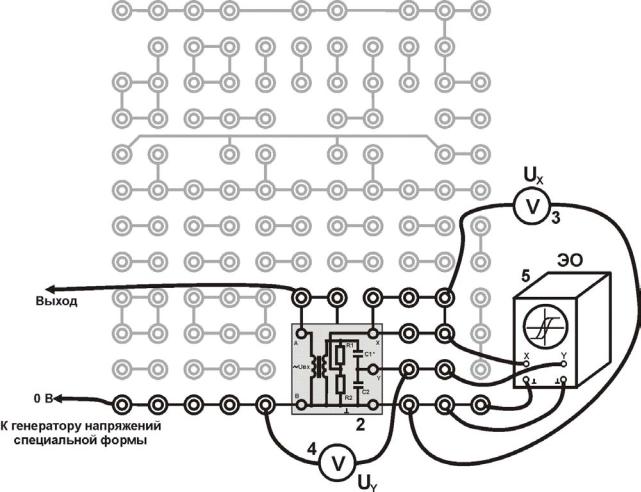
Электрическая схема установки показана на рис. 4, монтажная схема
– на рис. 5.
Установка для исследования свойств сегнетоэлектриков состоит из генератора сигналов специальной формы, миниблока «Сегнетоэлектрик» - 2, двух мультиметров - 3 и 4 и осциллографа - 5. В качестве исследуемого образца используется титанат бария (BaTiO) – сегнетоэлектрик, который служит изолятором в конденсаторе С1 .
Рис.5 Монтажная схема установки
П о р я д о к в ы п о л н е н и я р а б о т ы
Выполнение измерений
1. Соберите электрическую цепь по монтажной схеме, приведенной на рис. 5. Параметры установки занесите в таблицу 1.
Таблица 1
119
Параметры установки:
С |
2 |
= 6,80 мкФ, d = 3,20 10-3 |
м, s = 1,23 10-3 м2, R = 100 103 |
Ом, R |
= 10 103 |
Ом |
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
||||
U нас |
=...В |
Р =...Кл/ м2 |
U |
нас =...В |
|
Енас |
=...В/ м |
|
||||||||||
Y |
|
|
|
|
нас |
|
|
|
Х |
|
|
|
|
|
||||
yнас =...мм |
|
|
yост =...мм |
|
yS |
=...мм |
|
хнас =... |
мм |
|
|
хК =...мм |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Р |
|
=...Кл |
/ м2 |
|
|
Р =...Кл/ м2 |
|
|
ЕК |
=...В/ м |
|
||||||
|
|
ост |
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Включите кнопками «Сеть» питание блока генераторов напряжения
иблока мультиметров. Нажмите кнопку «Исходная установка» (поз. 19, см. рис. 1 на стр. 6). Загорится индикатор (поз. 6, см. рис. 1 на стр. 6) сигнала синусоидальной формы. Частота выходного сигнала установится 500Гц (см на индикатор - поз.5, рис. 1, стр. 6).
3.Включите осциллограф и выведите электронный луч в центр экрана.
4.Кнопками «Установка частоты 0,2 – 20 кГц » (поз. 10, см. рис. 1 на стр. 6) установите частоту 50 Гц.
5.Увеличивая напряжение в первичной обмотке трансформатора с помощью кнопок «Установка уровня выхода 0 … 15 В» (поз. 10, см. рис. 1 на стр. 6) генератора сигналов специальной формы (увеличивая напряжение UY примерно до 4,0 В), получите изображение предельной петли гистере-
зиса. Петля считается предельной, если рост напряжения не приводит к увеличению ее площади.
6. Ручками осциллографа ↔ и ↕ установите изображение петли симметрично относительно осей Х и У.
У |
|
Ручками осциллографа «Усиление Х», |
|||||
унас |
|
«Усиление У» (дискретно и плавно) |
|||||
|
|
|
|
|
|
|
|
уS |
|
установите наибольшие размеры пет- |
|||||
уост |
|
ли, которые вписываются в экран ос- |
|||||
|
|
циллографа. |
|
|
|
||
О |
Х |
7. По |
экрану |
осциллографа |
из- |
||
мерьте |
координаты точек |
хК , |
хнас , |
||||
хк |
хнас |
yост , yS |
, |
yнас (рис. 6). Мультиметрами |
|||
|
|
||||||
|
|
измерьте напряжения UYнас и U Хнас . |
Ре- |
||||
|
|
зультаты измерений занести в табл. 1. |
|||||
|
|
8. Кнопками «Установка уровня |
|||||
|
|
выхода 0 … 15 В» уменьшите напря- |
|||||
Рис. 7 |
|
жение UY |
до нуля. Этими же кнопка- |
||||
|
|
ми, повышая UY |
от нуля |
с шагом |
|||
примерно 0,40 В до его максимального значения UYнас , измерить соответствующие значения напряжения U X . Результаты измерений занести в табл. 2.
120
