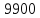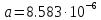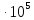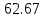Лабораторная работа - VTP
.docxЦЕЛЬ РАБОТЫ:
Изучить и освоить метод дискретного удовлетворения краевых условий для решения сопряжённой задачи теплообмена в ВТТУ. При помощи компьютера определить температурные поля участвующих в сопряжённом теплообмене тел, получить таблицы и графические зависимости, описывающие температурные поля.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ:
Теплообмен в системе печь-металл описывается уравнением
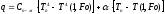 ,
(1)
,
(1)
где q - тепловой поток на обогреваемой поверхности металла Вт/м2; Тп –
температура печи, К; T(1,Fo) - температура обогреваемой поверхности металла, К; Fo - безразмерное время нагрева.
Математическая модель сопряжённой задачи теплообмена в камерной нагревательной печи
В качестве метода математического
моделирования используется метод
дискретного удовлетворения краевых
условий (ДУКУ). В соответствии с методом
ДУКУ тепловой поток и температура па
обогреваемой поверхности металла
соответственно имеют вид:
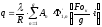 ,
,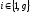 ,
(2)
,
(2)
 ,
(3)
,
(3)
где
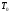 - начальная температура металла;
- начальная температура металла;
 - вспомогательные функции производной
на поверхности;
- вспомогательные функции производной
на поверхности;
 -
коэффициенты, определяемые дискретным
удовлетворением граничного условия
(1).
-
коэффициенты, определяемые дискретным
удовлетворением граничного условия
(1).
С учетом (2) и (3) уравнение (1) запишется в виде системы:
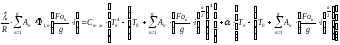 ,(4)
,(4)
где: g – число моментов времени, в которых удовлетворяются граничные условия. Дополнительно к системе (4) запишем уравнение достижения на поверхности металла в конце нагрева заданной конечной температуры, К:
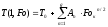 ,
(5)
,
(5)
Решением системы уравнений (4) и (5)
определяются неизвестные
 и
Тп, после чего рассчитываются
температуры поверхности и теплового
центра и перепад температур по сечению
металла в конце нагрева, К:
и
Тп, после чего рассчитываются
температуры поверхности и теплового
центра и перепад температур по сечению
металла в конце нагрева, К:
 ,
(6)
,
(6)
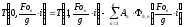 ,
(7)
,
(7)
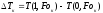 ,
(8)
,
(8)
Найдя решение сопряженной задачи теплообмена, температуру печи, а также температурное поле металла, можно рассчитать температуру газа в рабочем пространстве печи, исходя из равенства тепловых потоков в системе печь-металл и в системе газ-кладка-металл:
 ,
(9)
,
(9)
 ,
(10)
,
(10)
По известным значениям температуры
печи
 и температуры поверхности металла
и температуры поверхности металла
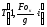 по формуле (9) рассчитываем тепловые
потоки
по формуле (9) рассчитываем тепловые
потоки
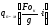 для “g” моментов времени.
А температура газа
для “g” моментов времени.
А температура газа
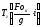 выражается из уравнения (10).
выражается из уравнения (10).
ХОД РАБОТЫ:
ИСХОДНЫЕ ДАННЫЕ
Тип углеродистой стали: 08кп;
Число заготовок: n=5;
Высота заготовок: b=0.2 м;
Ширина заготовок: a=0.2 м;
Длина заготовок: l=3.8м;
Коэффициент форма тела: k=1;
Эффективная степень черноты металла:

Температура металла в начале нагрева: Т0=293 К;
Температура металла в конце нагрева: Тк=1273 К;
Эффективная поверхность металла:

1.) Расчетный размер заготовки.
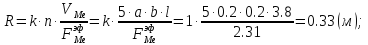
2.) Расчетное время нагрева металла.
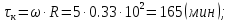
3.) Коэффициент температуропроводности.
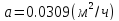
3.) Коэффициент теплопроводности.

4.) Коэффициент излучения с печи на металл.
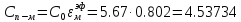 (Вт/м2·К4)
(Вт/м2·К4)
5.) Допустимый перепад температур.
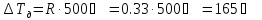
6.) Подготовили данные к расчету и занесли их в таблицу 1.
Таблица 1. Данные для расчета.
|
Наименование |
Значение |
Размерность |
|
Обозначение стали |
08 |
|
|
Число моментов времени, в которых удовлетворяются условия КУ |
g=5 |
|
|
Число уравнений в системе |
N=6 |
|
|
Ширина заготовки |
a=0.2 |
м |
|
Высота заготовки |
b=0.2 |
м |
|
Длина заготовки |
l=3.8 |
м |
|
Расчётный размер металла |
R= |
м |
|
Расчётное время нагрева металла |
τк= |
c |
|
Коэффициент температуропроводности |
|
м2/с |
|
Допустимая величина напряжения |
σд=35 |
кг/мм2 |
|
Коэффициент линейного расширения |
β=0.223 |
1/Сº |
|
Модуль упругости |
E=1.9 |
кг/мм2 |
|
Коэффициент теплопроводности |
λ=41.92 |
Вт/м·град |
|
Конечная температура металла |
T(1,F0)=1273 |
K |
|
Начальная температура металла |
T0=293 |
K |
|
Приведенный коэффициент излучения в системе печь-металл |
Сп-м=4.547 |
Вт/м2·К4 |
|
Коэффициент конвективной теплоотдачи |
α= |
Вт/м·К4 |
|
Допустимый перепад температур в конце нагрева |
ΔTд= |
град |
|
Приведенный коэффициент излучения в системе газ-кладка-металл |
Сг-к-м= |
Вт/м2·К4 |
Работа с программой
7.) Ввели данные в программу.
8.) Нашли значения температуры центра и поверхности металла, температуры газа, печи, тепловые потоки печь – металл и газ – металл, построила их графики (рис. 1, 2) с помощью программы.
Расчет по формулам
9.) Безразмерное время Фурье.
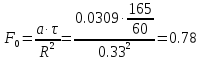
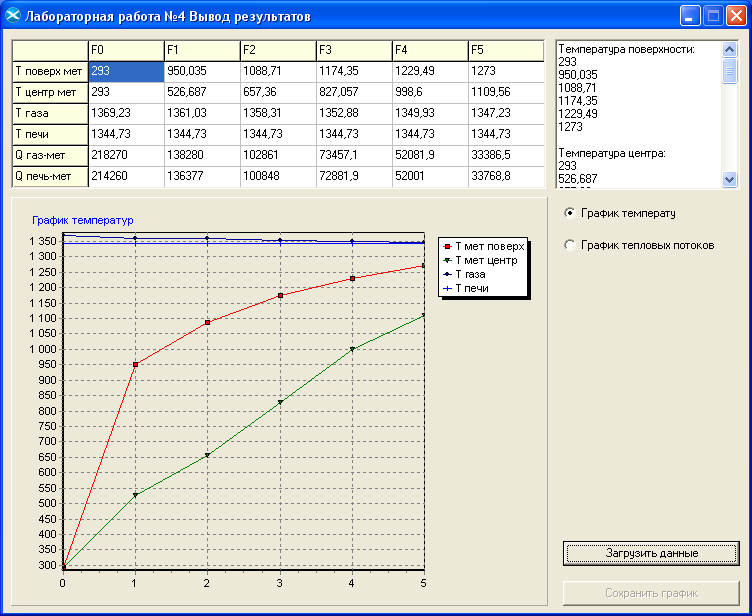
Рис.1. Рассчитанные данные и график температур
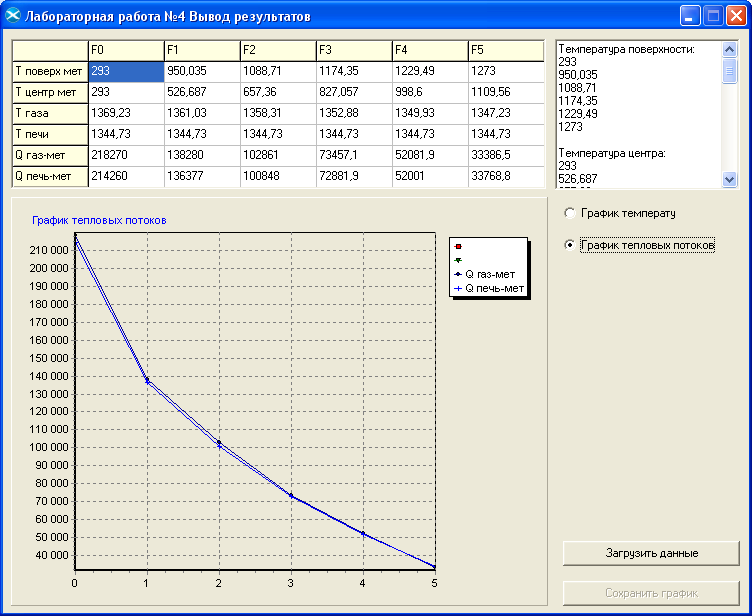
Рис.2. Рассчитанные данные и график тепловых потоков
10.) В таблицах специальных функций для расчета нагрева и охлаждения (Соколов А.К.) найдем значения вспомогательных функций.
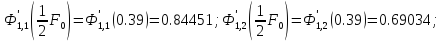

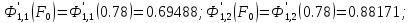
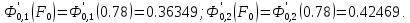
11.)
Запишем систему уравнений для определения
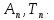
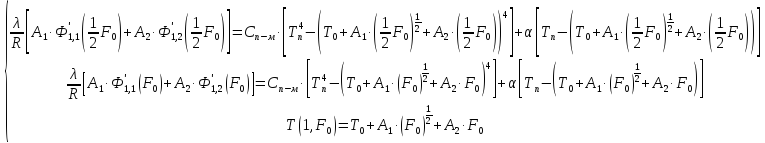
Решим систему в программе MathCAD.


Из предложенного списка корней выберем следующие:
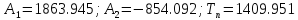 .
.
Сделаем проверку:
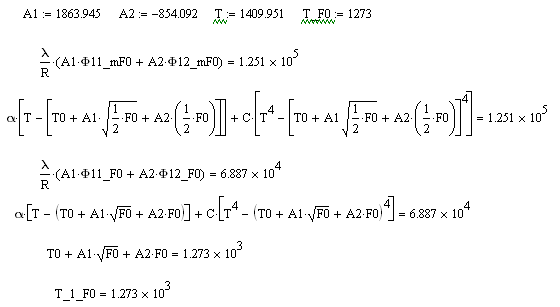
Таким образом, корни найдены верно.
12.) Рассчитаем температуры поверхности, теплового центра и перепад температур по сечению металла в конце нагрева.

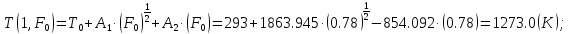
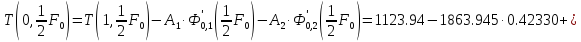


13.) Рассчитаем тепловой поток в системе печь-металл.
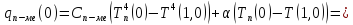

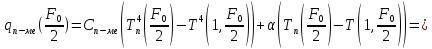
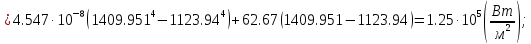


14.) Рассчитаем температуры газа.

Решим данную систему уравнений в программе Matchad.

Из предложенного списка корней выберем следующий:


Решим данную систему уравнений в Matchad.

Из предложенного списка корней выберем следующий:

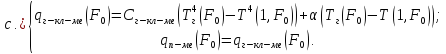
Решим данную систему уравнений в Matchad.
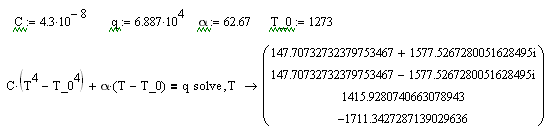
Из предложенного списка корней выберем следующий:

15.) Построим температурные поля.
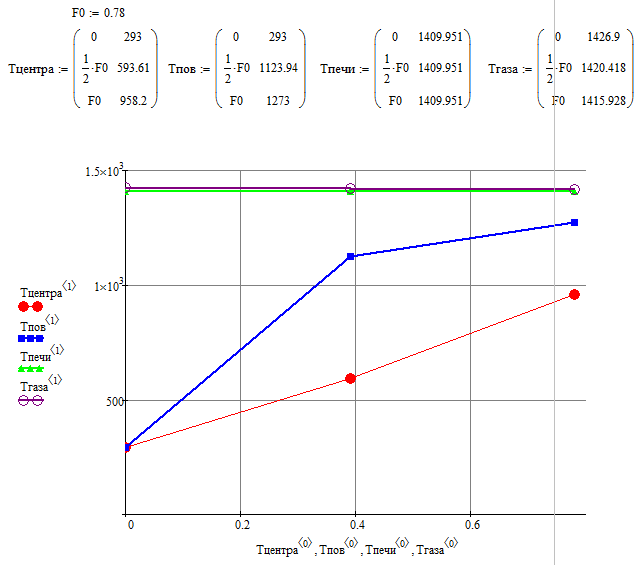
Вывод: В данной лабораторной работе мы изучили и освоили метод дискретного удовлетворения краевых условий для решения сопряжённой задачи теплообмена в ВТТУ. При помощи компьютера определили температурные поля, участвующие в сопряжённом теплообмене тел, получили таблицы и графические зависимости, описывающие температурные поля. Рассчитали температурные поля и тепловые потоки по методу ДУКУ для двух моментов времени.