Лабораторная работа № 1- Операции с векторами. Основы трехмерной графики

Лабораторная работа №1

Операции с векторами. Основы трехмерной графики

Цель работы. Изучение операций с векторами и основ трехмерной компьютерной графики.

Задание. 1. Для двух векторов и , где N номер варианта, вычислить их сумму (), разность (), cкалярное произведение (), векторное произведение (), модули (), косинус угла между векторами , смешанное произведение .

Рис. B

Рис. A

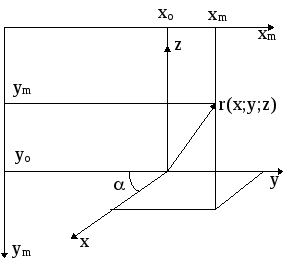
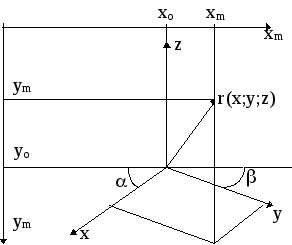
2. Построить на экране два вектора в системе координат, аналогичной рис.1 для четных вариантов, рис.2 - для нечетных.

Углы  и  выбрать самостоятельно.

Математическое описание. Вектором называется направленный отрезок прямой. В декартовой системе координат x,y,z вектор однозначно определяется тремя проекциями или . Основные расчетные формулы для декартовой системы координат приведены ниже.

1. Сумма векторов: .

2. Разность: .

3. Скалярное произведение: .

4. Модули: .

5. Векторное произведение: .

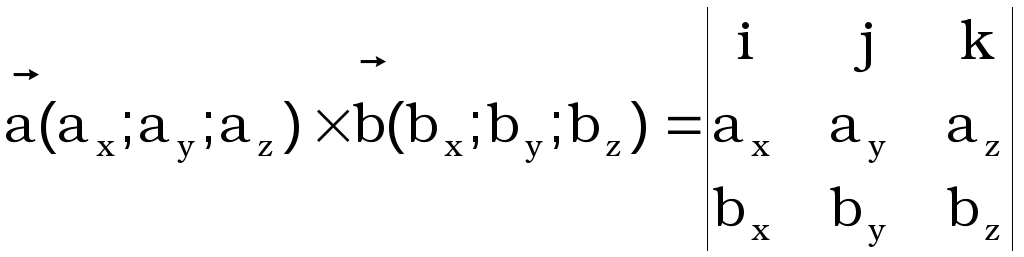6. Косинус угла между векторами: .

7. Смешанное произведение: .

8. Условимся координаты точки в декартовой системе координат (x;y;z) называть физическими, а координаты точки на дисплее (x_m;y_m) - машинными. Для выполнения графических операторов на компьютере необходимо пересчитать три физические координаты точки (x;y;z) в две машинные координаты (x_m;y_m) по формулам (1)-(2) или (3)-(4) для систем координат рис.1 или рис.2, соответственно , (1) , (2) , (3) , (4) где x,y,z - физические координаты точки, x_m,y_m - машинные координаты, x₀,y₀ - машинные координаты начала физической системы координат, М_x,М_y - масштабы по осям x и y соответственно, которые показывают, сколько машинных точек (пикселей) составляют одну физическую единицу.

Содержание отчета.

1. Название, цель работы и задание.

2. Структограмма и распечатка программы.

3. Результаты расчета, графическое изображение двух векторов, выводы по работе.

- 5 -