Лабораторная работа № 3- Решение одномерных оптимизационных задач

Лабораторная работа №3

Решение одномерных оптимизационных задач

Цель работы. Изучение численных методов решения одномерных оптимизационных задач.

Задание. Численно двумя методами (табл.1) и аналитически решить одномерную оптимизационную задачу: .

Таблица 1

Вариант	Методы
1,4,7,10,13,16,19,22,25,28	перебора, половинного деления
2,5,8,11,14,17,20,23,26,29	перебора, перебора с переменным шагом
3,6,9,12,15,18,21,24,27,30	перебора, золотого сечения

Математическое описание. Решение оптимизационной задачи F(x)Þmax(min) - определение оптимального значения параметра оптимизации (x), которому соответствует экстремальное значение целевой функции. Целевая функция F(x)- это функция, экстремальное значение которой ищем. Параметр оптимизации (x) - аргумент целевой функции.

Рис.4

1. Аналитический метод.

Необходимое условие. Функция y=F(x) может иметь экстремум только в точках, в которых первая производная равна нулю . Эти точки называются критическими.

Достаточное условие. Положительное значение второй производной в критической точке соответствует минимуму целевой функции, отрицательное - максимуму, равенство нулю - необходимости дополнительных исследований.

Замечание. Методы, рассмотренные ниже, предназначены для отыскания минимума целевой функции. Нахождение максимума функции можно свести к отысканию минимума функции с противоположным знаком (рис.4).

Рис.5

Рис.6

2. Метод перебора (или метод равномерного распределения точек по отрезку). Задаемся начальным значением x=x₀ и шагом поиска h, который определяет и точность численного метода. Пока F(x) больше F(x+h), увеличиваем значение аргумента на шаг x_i+1=x_i+h. Суть мето-да проиллюстрирована на рис.5, структо-грамма приведена на рис.6.

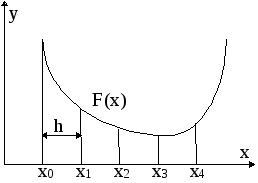
Рис.7

3. Метод перебора с переменным шагом (поразрядное приближение). Метод перебора повторяем несколько раз с разным шагом, который уменьшаем по мере приближения к решению. Суть метода заключается в следующем. Задаемся начальным значением параметра x=a, шагом h и точностью расчета e. Методом перебора с заданным шагом осуществляем поиск корня. После этого аргумент уменьшаем на величину шага, шаг уменьшаем в к раз и повторяем метод обычного перебора. Расчет выполняем, пока шаг больше точности. Структограмма метода приведена на рис.7.

Рис.8

Рис.9

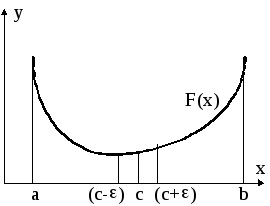
4. Метод дихотомии или половинного деления. Задаем интервал (a,b), на котором существует одно решение оптимизационной задачи, и точность e. Вычисляем середину отрезка . Если F(x+e)>F(x-e), то переносим в середину правую границу интервала поиска (b=c), иначе - левую (a=c). Вычисления повторяем, пока ширина интервала (a,b) больше точности. Суть метода проиллюстрирована на рис.8, структограмма приведена на рис.9.

Рис.10

Рис.11

5. Метод золотого сечения. Деление отрезка [a,b], на котором существует одно решение задачи, производим таким образом, чтобы отношение длины отрезка к длине большей его части было равно отношению большей части к меньшей. Такое деление называется золотым сечением и позволяет использовать результаты расчета целевой функции на следующем шаге вычислений. Это сокращает время счета примерно в полтора раза по сравнению с методом половинного деления (подумайте, почему?). Порядок выполнения расчета следующий. Задаем отрезок [a,b] с одним решением и точность . Выбираем две промежуточные точки d=a+0,382(b-a), c=a+0,618(b-a) (попробуйте коэффициенты 0,382 и 0,618 вывести самостоятельно из правила золотого сечения). Вычисляем значения целевой функции в промежуточных точках Fc=F(c), Fd=F(d). Если Fc>Fd, то b=c; c=d; Fc=Fd; d=a+0.382(b-a); Fd=F(d). Если Fc<Fd, то a=d; d=c; Fd=Fc; c=a+0.618(b-a); Fc=F(c). Пока длина интервала поиска больше точности, вычисления повторяем. Суть метода проиллюстрирована на рис.10, алгоритм приведен на рис.11.

Содержание отчета.

1. Название, цель работы и задание.

2. Математическое описание, алгоритм и текст программы.

3. Результаты численного (2 метода) и аналитического решений, выводы.

- 15 -