
ALL_
.DOCСодержание.
|
Тема1. Решение системы обыкновенных дифференциальных уравнений. Задача Коши……………………………………………………………………………. |
|
|
Постановка задачи…………………………………………………………………….. |
|
|
Алгоритм………………………………………………………………………………… |
|
|
Варианты………………………………………………………………………………… |
|
|
Тема2. Решение системы обыкновенных дифференциальных уравнений. Краевая задача………………………………………………………………………… |
|
|
Постановка задачи…………………………………………………………………….. |
|
|
Алгоритм…………………………………………………………………………………. |
|
|
Варианты………………………………………………………………………………… |
|
|
Тема3. Уравнение теплопроводности. Явная и неявная схемы………………. |
|
|
Постановка задачи…………………………………………………………………….. |
|
|
Алгоритм…………………………………………………………………………………. |
|
|
Варианты………………………………………………………………………………… |
|
|
Тема4. Волновое уравнение. Уравнение гиперболического типа…………….. |
|
|
Постановка задачи…………………………………………………………………….. |
|
|
Алгоритм…………………………………………………………………………………. |
|
|
Варианты………………………………………………………………………………… |
|
|
Тема5. Стационарное уравнение…………………………………………………… |
|
|
Постановка задачи…………………………………………………………………….. |
|
|
Алгоритм…………………………………………………………………………………. |
|
|
Варианты………………………………………………………………………………… |
|
|
Тема6. Методы оптимизации.ю……………………………………………………… |
|
|
Постановка задачи…………………………………………………………………….. |
|
|
Алгоритм…………………………………………………………………………………. |
|
|
Варианты………………………………………………………………………………… |
|
Задание № 1.
Тема: Решение системы обыкновенных дифференциальных уравнений. Задача Коши.
Постановка задачи.
Алгоритм.
Задание:
Решить задачу Коши методами Эйлера, Рунге–Кутта 2, Руне–Кутта 4 и прогноз–коррекции.
Варианты.
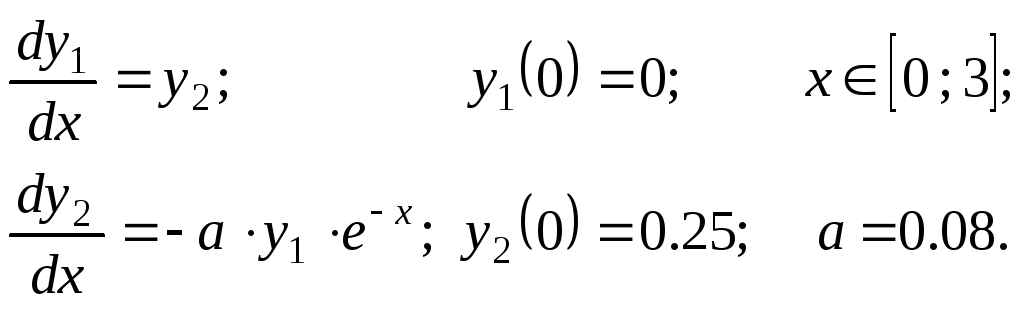

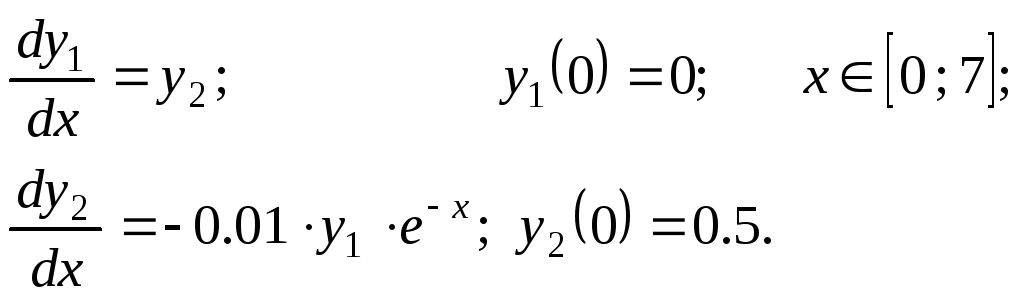
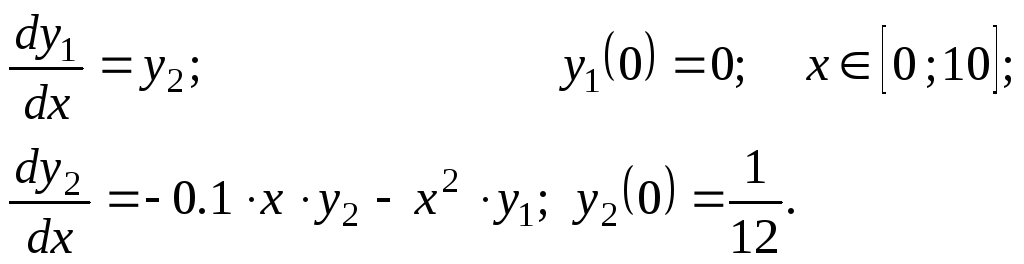







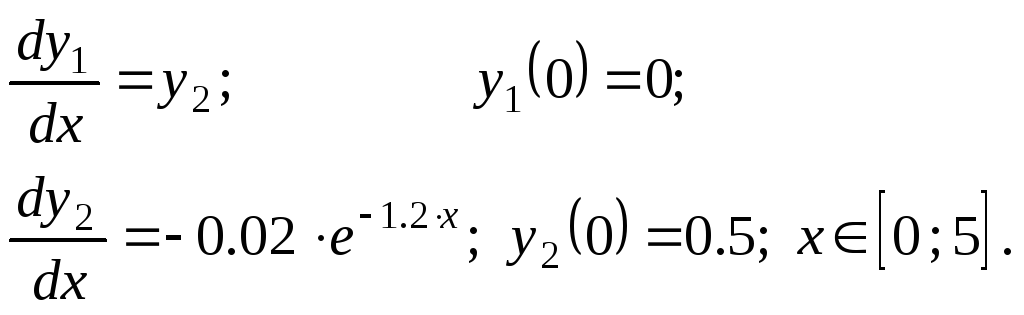


![]()

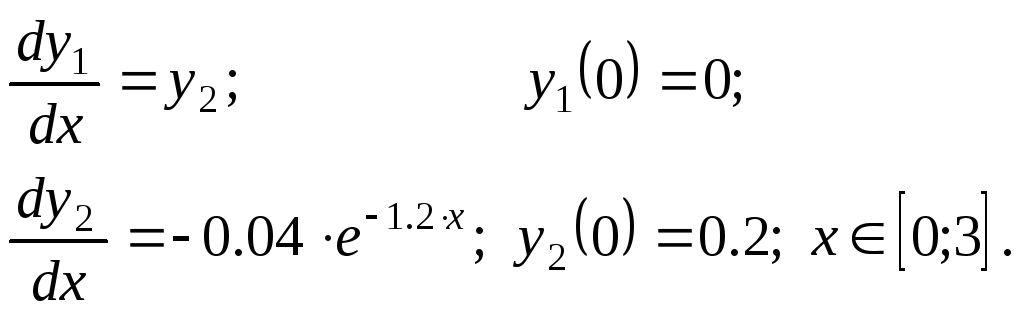

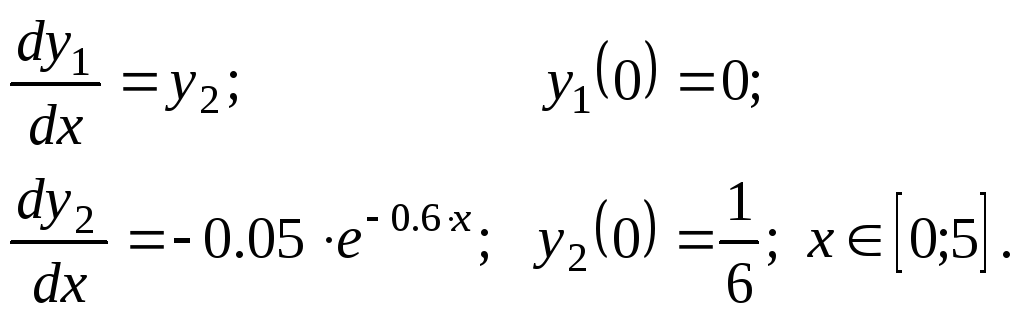

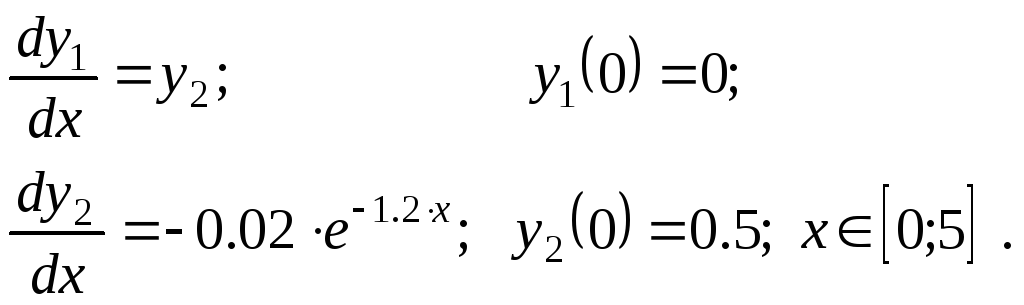

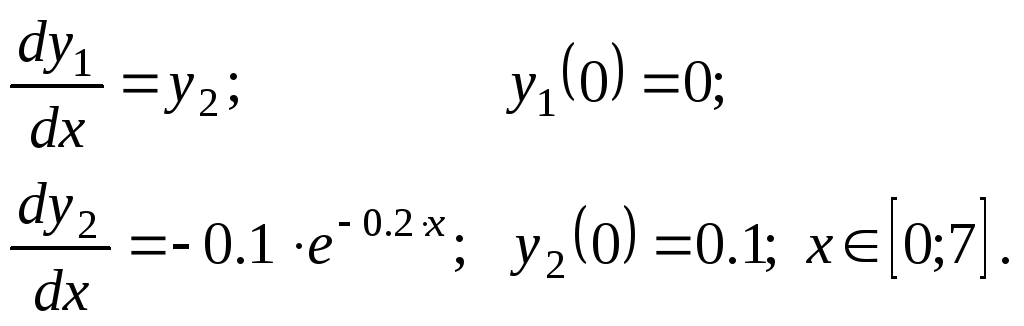

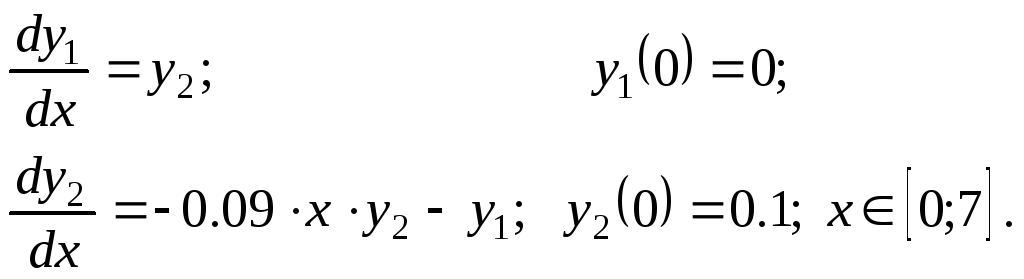
Задание № 2.
Тема: Решение системы обыкновенных дифференциальных уравнений. Краевая задача.
Постановка задачи.
Пусть дано обыкновенное дифференциальное уравнение второго порядка:
![]()
Простейшая двухточечная краевая задача для уравнения (1) ставится следующим образом:
Требуется найти
функцию
![]() ,
которая внутри отрезка
,
которая внутри отрезка
![]() удовлетворяет уравнению (1),
а на концах отрезка – краевым условиям:
удовлетворяет уравнению (1),
а на концах отрезка – краевым условиям:
![]()
Алгоритм метода прогонки для краевой задачи.
-
Описание и инициализация массивов и переменных:
![]()
-
Определение массивов:
![]()
![]()
-
Вычисление
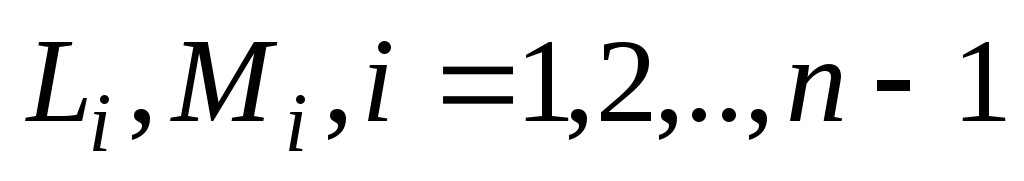 по формулам:
по формулам:
![]()
![]()
- прямой ход прогонки.
-
Вычисление
 по формуле:
по формуле:
![]()
-
Вычисление
 по формуле:
по формуле:
![]() - обратный ход
прогонки
- обратный ход
прогонки
-
Печать вычисленных значений.
Задание:
-
Используя метод прогонки, решить краевую задачу для обыкновенного дифференциального уравнения; шаг h=0.05
-
Используя метод конечных разностей, решить краевую задачу для обыкновенного дифференциального уравнения; h–шаг; h=0.1
Варианты.
-
 2.
2. 
-
 4.
4. 
-
 6.
6. 
-
 8.
8. 
-
 10.
10. 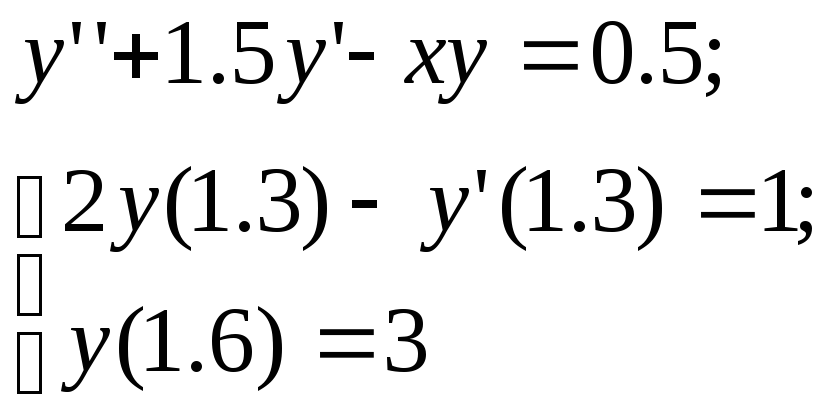
-
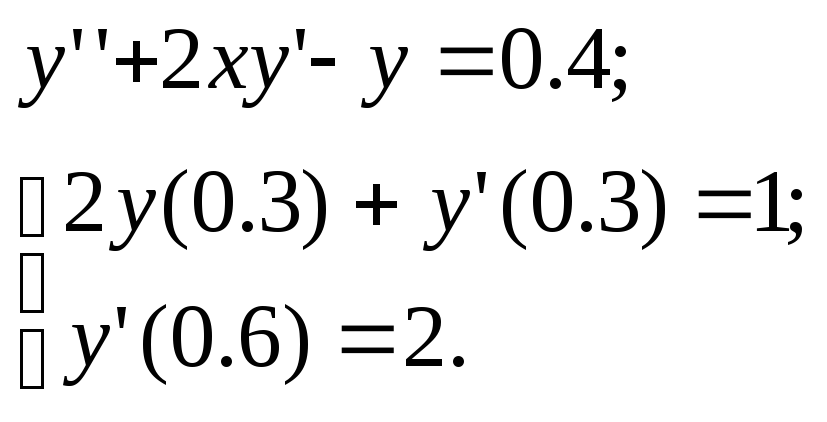 12.
12. 
-
 14.
14. 
-
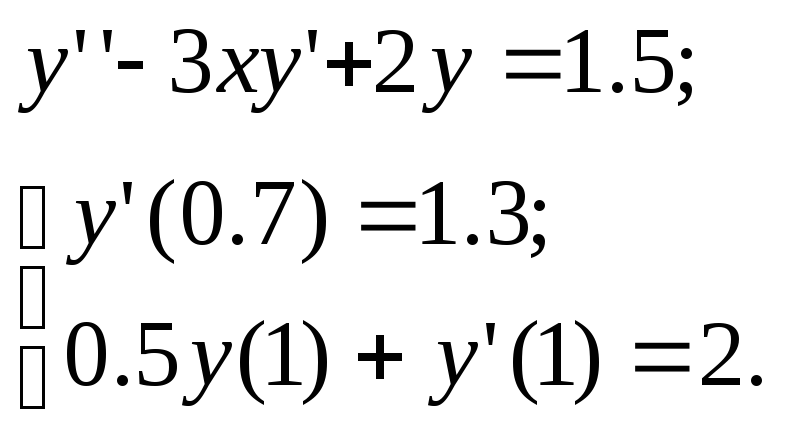 16.
16. 
-
 18.
18. 
-
 20.
20. 
-
 22.
22. 
-
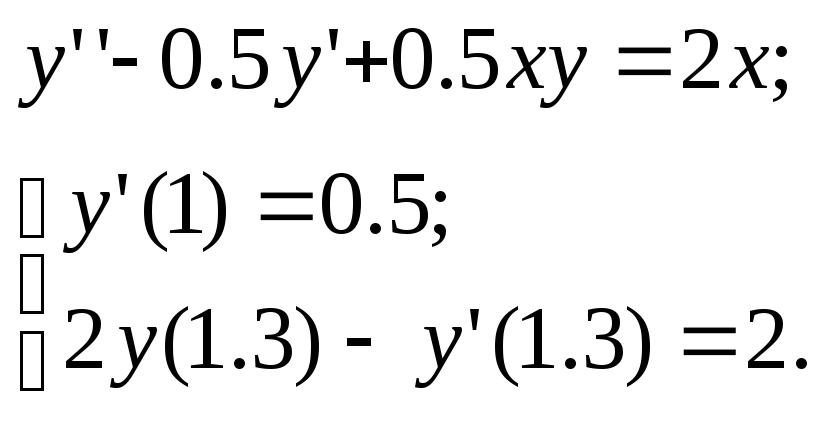 24.
24. 
-
 26.
26. 
-
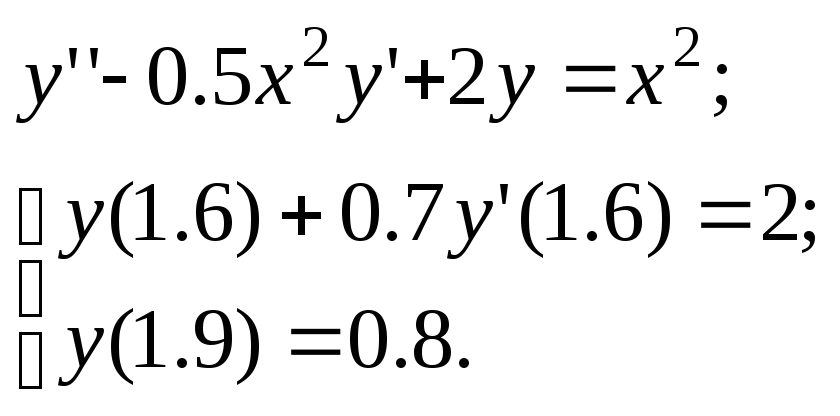 28.
28. 
-
 30.
30. 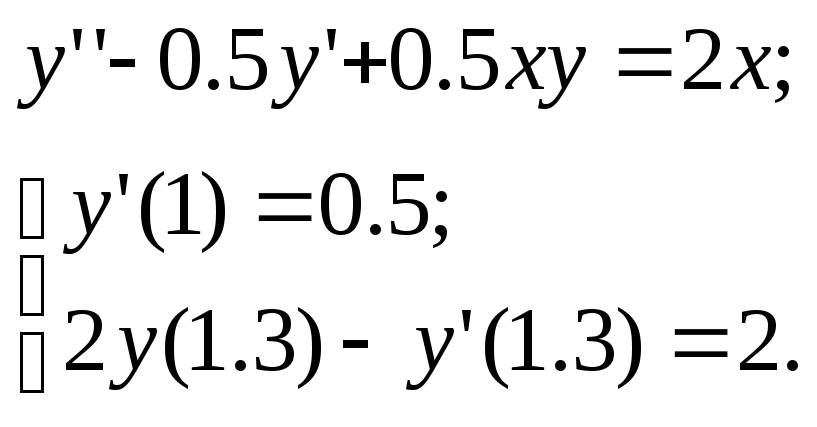
-
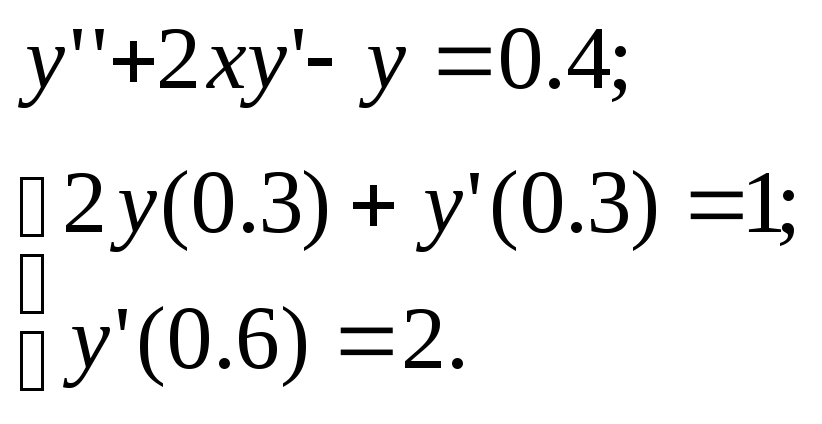 32.
32. 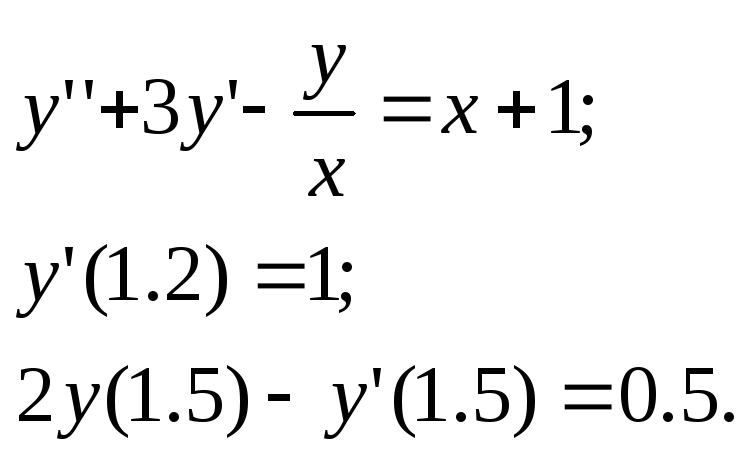
-
 34.
34. 
Задание № 3.
Тема: Уравнение теплопроводности. Явная и неявная схемы.
Постановка задачи.
Алгоритм.
Задание:
Используя метод сеток, решить смешанную задачу для дифференциального уравнения параболического типа
![]() (уравнение
теплопроводности)
(уравнение
теплопроводности)
при заданных начальных условиях:
![]()
![]()
![]() ,
где
,
где
![]()
Решение
выполнить при h=0.1,
для
![]() ,
,
![]() =1.0.
=1.0.
Использовать:
-
Явную схему;
-
Неявную схему.
Варианты.
1. 2. 3.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() .
. ![]() .
. ![]() .
.
4. 5. 6.
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() .
. ![]() .
. ![]()
7. 8. 9.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() .
. ![]() .
. ![]() .
.
10. 11. 12.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() .
. ![]() .
. ![]() .
.
13. 14. 15.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() .
. ![]() .
. ![]() .
.
16. 17. 18.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() .
. ![]() .
. ![]() .
.
19. 20. 21.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() .
. ![]() .
. ![]() .
.
22. 23. 24.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() .
. ![]() .
. ![]() .
.
Задание № 4.
Тема: Волновое уравнение. Уравнение гиперболического типа.
Постановка задачи.
Алгоритм.
-
Вводим шаг по оси x:
h и определяем число точек по оси x – k:
![]() .
.
-
Вводим шаг по времени τ. Условие устойчивости вычислений : τ < h (можно τ ≤ h).
 ;
;
 .
. -
Создаем массивы смещений:
![]() -
значения
смещений при
-
значения
смещений при
![]()
![]() -
значения смещений при
-
значения смещений при
![]()
![]() -
значения смещений при
-
значения смещений при
![]()
Т.е. будем использовать следующие обозначения:
![]() обозначаем
обозначаем
![]() ,
,
![]() обозначаем
обозначаем
![]() ,
,
![]() обозначаем
обозначаем
![]() .
.
-
Заполняем массивы при
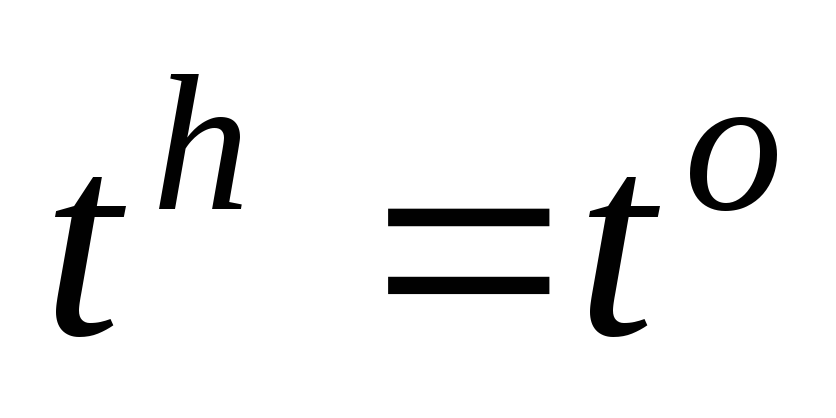 :
:
![]() и
и
![]() ,
,
![]() .
.
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
-
Определяем значения смещений на границах:
![]() ,
,
![]() ,
где
,
где
![]() .
.
-
Строим график зависимости смещения от координаты в начальный момент времени:


-
Организуем цикл по времени от
 до
до
 с шагом τ.
На каждой итерации цикла будем выполнять
следующее:
с шагом τ.
На каждой итерации цикла будем выполнять
следующее:-
Делаем шаг по времени
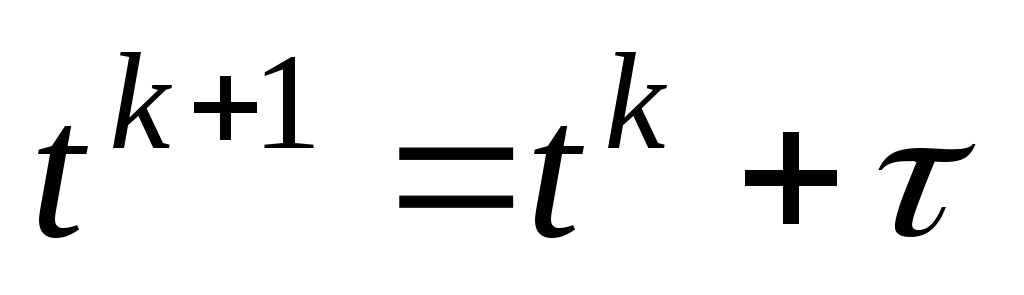 ;
; -
Организуем цикл по x от
 до
до
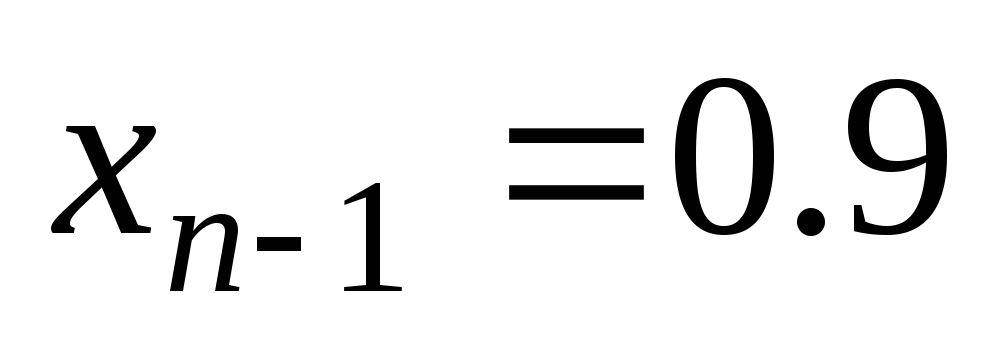 шагом
шагом
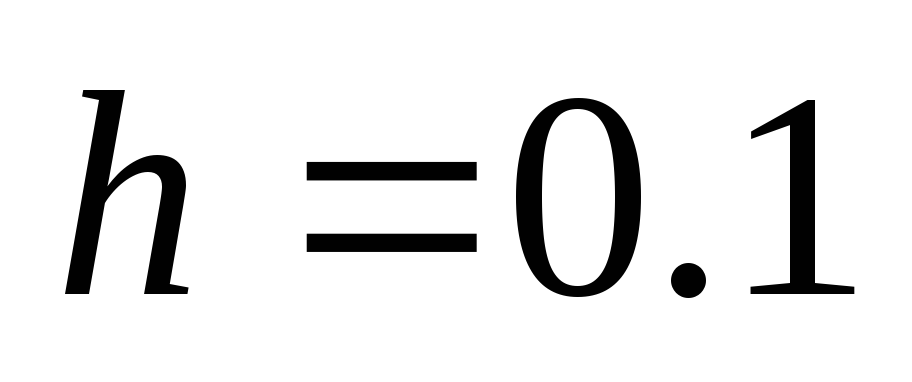 (или организуем цикл по точкам от i
= 2 до
i
= n-1,то
есть i
принимать значения i
= 2,3,4,…,n-1)
и вычислим новые значения смещений,
которые запишем в вспомогательный
массив
(или организуем цикл по точкам от i
= 2 до
i
= n-1,то
есть i
принимать значения i
= 2,3,4,…,n-1)
и вычислим новые значения смещений,
которые запишем в вспомогательный
массив
 ,
по формуле:
,
по формуле:
-
![]() ;
;
![]() .
.
-
Вычислим новые значения смещений в краевых (граничных) точках по формулам:
![]() ; //
; // ![]()
![]() ; //
; // ![]()
-
Рисуем график зависимости смещения от координаты для нового момента при времени
 .
. -
Переприсваиваем значения смещений:
1)
Значения
![]() присваиваются переменной
присваиваются переменной
![]() :
:
![]() ,
,
![]() или
или
![]() .
.
2)
Значения
![]() присваиваются переменной
присваиваются переменной
![]() :
:
![]() ,
,
![]() .
.
-
Проверяем условия окончания итерационного процесса по времени:
![]() ?
?
Если условие истинно, то переходим к пункту 7.0.
Иначе:
-
Конец вычислений.
Алгоритм.
1*. Дискретизация пространства и времени – 1 и 2.
2*. Описание переменных – 3.
3*. Определение смещений в начальный момент времени:
во внутренних точках – 4, на границах исследуемого участка – 5.
4*. Вывод графика U(x,0) – 6 .
5*. Основной цикл по времени – 7, включающий в себя:
-
Определение
 - 7.0;
- 7.0; -
Вычисление новых значений смещений во внутренних точках – 7.1, на границах – 7.2;
-
Вывод графика
 - 7.3;
- 7.3; -
Переприсваивание значений – 7.4;
-
Проверка условия окончания цикла по времени – 7.5.
6*. Конец вычислений.
Задание:
Используя метод сеток, решить задачу для управления колебания струны
![]()
с начальными условиями:
U(x,0)=f(x),
![]()
0 ≤ x ≤ 1;
и краевыми условиями:
U(0,t)=φ(t),
U(1,t)=ψ(t),
c=1.0;
Решение выполнить с шагом h = 0.1.
Варианты.
1. 2.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
. ![]() .
.
-
4.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
. ![]() .
.
-
6.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
