Рассмотрим тороид, намотанный на сердечник из однородного и изотропного магнетика. Если по тороиду пропустить ток I, то внутри него возникнет магнитное поле, которое можно рассчитать с помощью теоремы о циркуляции вектора .

Из соображений симметрии ясно, что линии вектора поля тороида представляют собой окружности, центры которых расположены на оси вращения 00 тора. Ось 00 проходит через точку 0, перпендикулярно к плоскости чертежа (рис. 8). Направление линий связано с направлением тока I в витках обмотки правилом правого винта. Поэтому при расчете поля внутри тороида в качестве контура интегрирования L удобно взять одну из таких линий с произвольным радиусом r. Направление обхода контура L выбирается одинаковым с направлением линии (рис. 8). Тогда на основании теоремы о циркуляции вектора можно записать:

, (13)

где N – число витков в обмотке тороида (все витки охватываются контуром интегрирования). Учитывая, что модуль вектора во всех точках такого контура будет постоянным, выражение (13) можно переписать следующим образом:

или

. (14)

Откуда находим выражение для H:

. (15)

Анализ формулы (15) показывает, что магнитное поле внутри тороида в общем случае неоднородно – напряженность поля H уменьшается при увеличении r от до :

, (16)

, (17)

где – диаметр витков обмотки тороида.

Если контур интегрирования выбрать в виде окружности с центром, лежащим на оси 00, и радиусом , то он вообще не охватит витков обмотки с током (NI=0). Поэтому, согласно (13), в области, для которой выполняется неравенство , напряженность магнитного поля H=0.

Если контур интегрирования выбрать в виде окружности с радиусом , то алгебраическая сумма токов в витках обмотки, охватываемых контуром, равна NI-NI=0 и, согласно (13), в области, в которой , напряженность магнитного поля H=0. Следовательно, вне тороида магнитного поля нет.

Напряженность магнитного поля на средней линии тороида

(18)

где – длина средней линии тороида.

Если увеличивать средний радиус тороида , сохраняя диаметр его витков d и число витков на единицу длины , то неоднородность поля внутри тороида будет уменьшаться. При тороид называют тонким, а поле в нем будет практически неизменным по модулю .

Экспериментальная часть

1. Метод измерений

Магнитная проницаемость ферромагнетиков зависит от напряженности магнитного поля. По этой причине от величины зависят и те характеристики контура электрической цепи, которые связаны с магнитной проницаемостью ферромагнитного сердечника, например индуктивность тороида

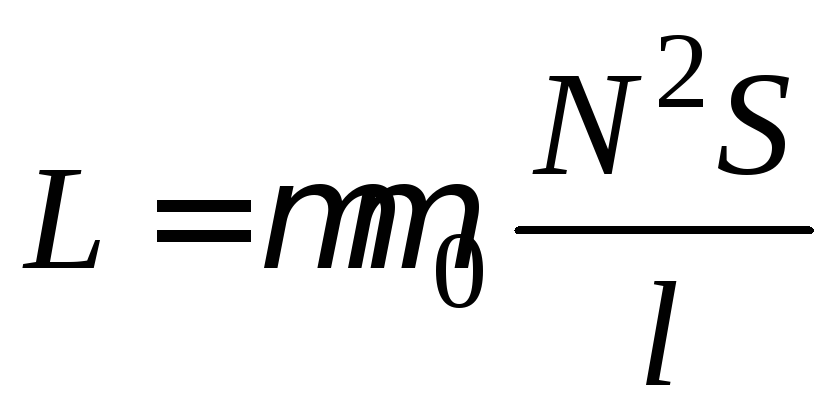(19)

и его индуктивное сопротивление переменному току

, (20)

где – магнитная постоянная; – число витков тороида, – площадь поперечного сечения сердечника тороида; – длина средней линии сердечника тороида; – циклическая частота переменного тока.

В данной работе измерение магнитной проницаемости сердечника основано, согласно формуле (19), на измерениях индуктивности тороида и его геометрических параметров , и . Для определения индуктивности достаточно измерить индуктивное сопротивление тороида переменному току известной частоты . Полное сопротивление тороида переменному току

. (21)

Так как обычно , то величиной активного сопротивления тороида можно пренебречь по сравнению с индуктивным сопротивлением переменному току частоты 200 Гц.

Закон Ома позволяет определить величину путем измерений тока и напряжения на участке цепи, содержащем тороид:

. (22)

Расчетная формула для определения магнитной проницаемости , полученная с использованием выражений (19), (20), (21), (22), имеет следующий вид:

, (23)

где – постоянная установки.

Напряженность магнитного поля, которое создается в тороидальном сердечнике при протекании по обмотке тока , можно приближенно рассчитать по формуле (18)

. (24)

Таким образом, каждому значению тока I соответствуют определенная напряженность магнитного поля магнитная проницаемость сердечника и индукция магнитного поля :

. (25)

Определяя величины , и при различных токах, можно экспериментально установить следующие зависимости:

а) – зависимость магнитной индукции от напряженности магнитного поля (основная кривая намагничивания ферромагнетика);

б) – зависимость магнитной проницаемости сердечника от напряженности магнитного поля.

2. Описание экспериментальной установки

Электрическая схема установки показана на рис. 9, монтажная –

на рис.10.

Рис. 9. Электрическая схема:

1 – генератор сигналов специальной формы;

2 – мультиметр (режим  , входы COM, mA);

3 – блок «Сопротивление», = 100 Ом;

4 – мультиметр (режим V 2 V, входы COM, VΩ);

5 – тороидальный сердечник с обмотками и ;

6 – блок «Ферромагнетик».

На тороидальный сердечник 5, изготовленный из исследуемого ферромагнитного материала, намотаны проволочных витков. Эта обмотка, по которой пропускают переменный ток частоты 200 Гц, служит для намагничивания ферромагнетика, и по ее параметрам определяют напряженность намагничивающего поля. Генератор сигналов специальной формы 1 позволяет изменять напряжение , а следовательно, и ток в обмотке тороида. Эти величины измеряют соответственно вольтметром 4 и миллиамперметром 2.

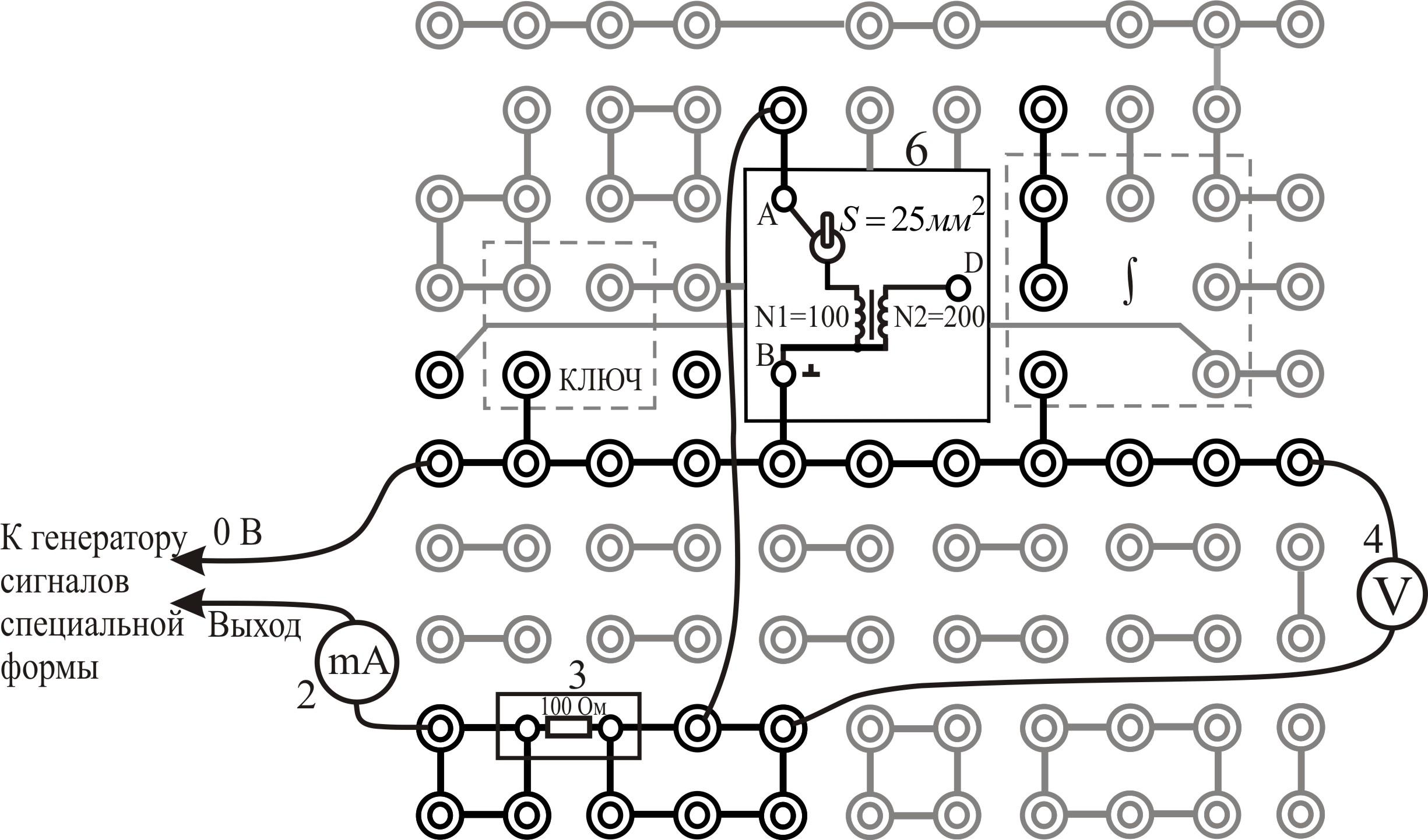
Рис. 10. Монтажная схема: 2 – мультиметр(режим  , входы COM, mA);

3 – блок «Сопротивление», = 100 Ом; 4 – мультиметр (режим V  2 V, входы COM, VΩ); 6 – блок «Ферромагнетик».