
- •Теоретические сведения к заданию 1
- •Классический метод расчета переходных процессов
- •Для последовательной цепи, содержащей линейные резисторR, катушку индуктивности l и конденсатор с, при ее подключении к источнику с напряжением u (см. Рис. 1.41) можно записать
- •Подставив в (1.1) значение тока через конденсатор
- •В общем случае уравнение, описывающее переходный процесс в цепи с nнезависимыми накопителями энергии, имеет вид
- •Начальные условия. Законы коммутации
- •Общая методика расчета переходных процессов классическим методом
- •Примеры расчета переходных процессов классическим методом
- •1. Переходные процессы в r-l цепи при ее подключении к источнику напряжения
- •2. Переходные процессы при отключении катушки индуктивности от источника питания
- •3. Заряд и разряд конденсатора
- •Энергии и произвольным числом резисторов
- •Переходные процессы при подключении последовательной r-l-c-цепи к источнику напряжения
- •В этом случае
- •Некоторые свойства изображений
- •Изображения производной и интеграла
- •Закон Ома в операторной форме
- •Для мгновенных значений переменных можно записать
- •Законы Кирхгофа в операторной форме Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю:
- •Переход от изображений к оригиналам
- •Например, для изображения тока в цепи на рис. 1.61 можно записать
- •Последовательность расчета переходных процессов операторным методом
- •Формулы включения
- •В результате
- •Сведение расчета переходного процесса к расчету с нулевыми начальными условиями
- •Метод переменных состояния
- •Методика составления уравнений состояния на основе принципа наложения
- •Решение
- •Решение
Решение
Векторы Х и Y для данной схемы
Х
![]() ;
;
Y
![]() .
.
Тогда уравнения состояния
 (1.29)
(1.29)
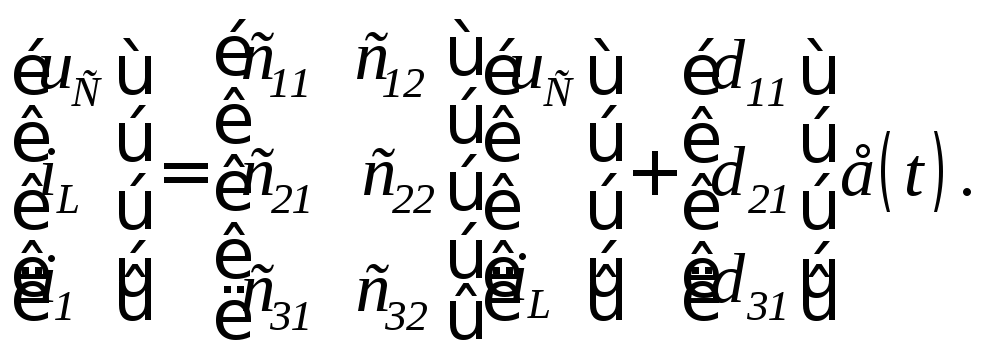 (1.30)
(1.30)
Для нахождения элементов матриц А, В, С и D заменим катушку индуктивности в коммутационной цепи на источник тока
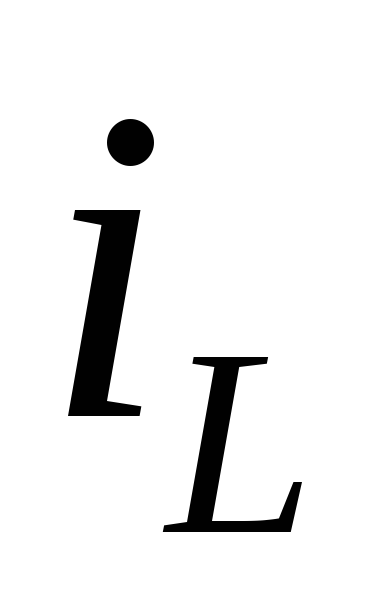 ,
а конденсатор
на источник ЭДС
,
а конденсатор
на источник ЭДС
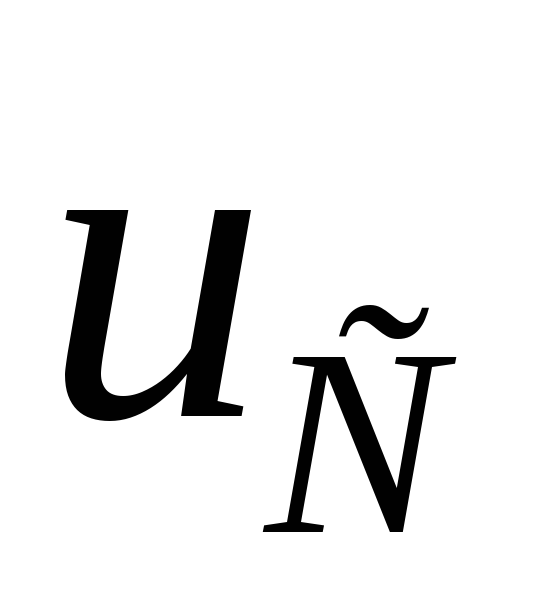 .
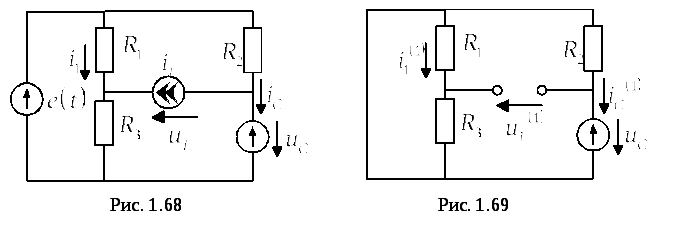
В результате получим резистивную схему
на рис. 1.68.
.
В результате получим резистивную схему
на рис. 1.68.
 Используя
принцип суперпозиции, рассмотрим три
частичные схемы, в каждой из которых
действует только один источник ЭДС или
тока.
Используя
принцип суперпозиции, рассмотрим три
частичные схемы, в каждой из которых
действует только один источник ЭДС или
тока.
Первая частичная схема приведена на рис. 1.69. В ней оставляем только источник ЭДС, соответствующий напряжению
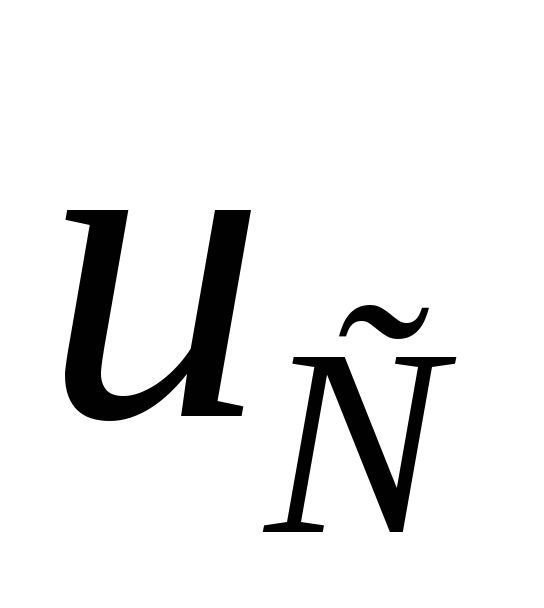 на конденсаторе.
на конденсаторе.
Из
анализа схемы следует, что
![]() ;
;![]() ;
;![]() или
или
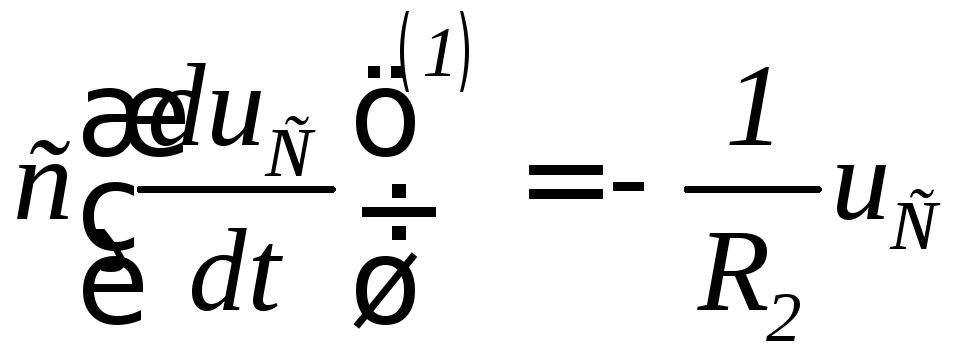 ;
;
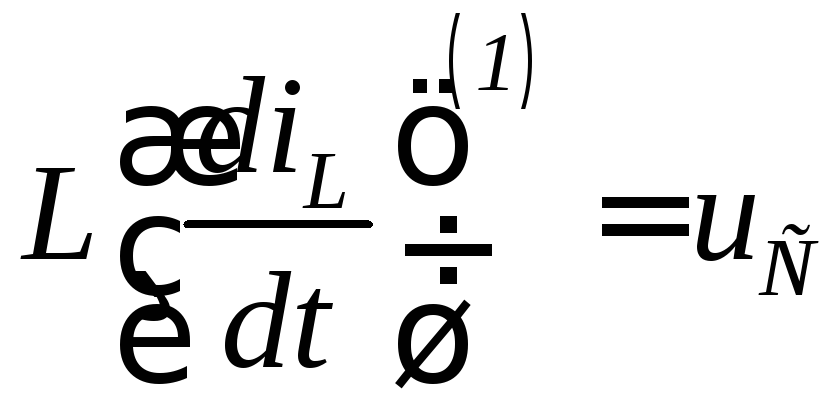 .
.
Отсюда
получаем
![]() ;
;![]() ;
;![]() .
.
В
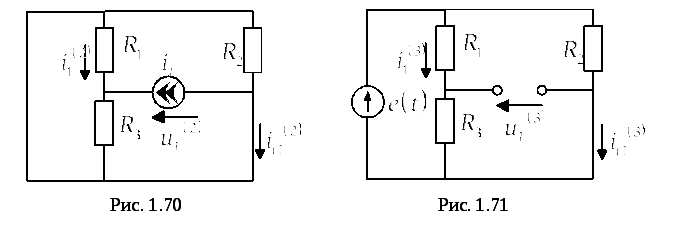 торая
частичная схема представлена на рис.
1.70. В ней оставляем только источник
тока, соответствующий току
торая
частичная схема представлена на рис.
1.70. В ней оставляем только источник
тока, соответствующий току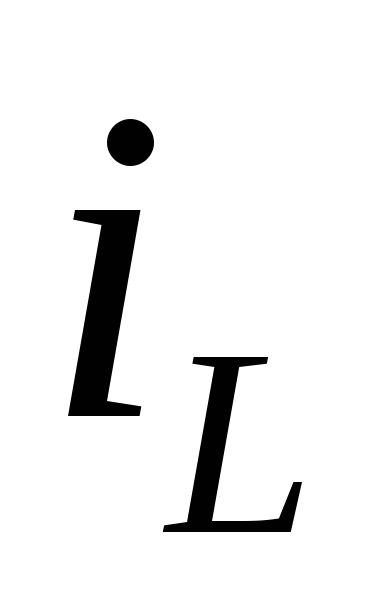 катушки индуктивности.
катушки индуктивности.
Для
этой схемы
![]() ;
;![]() ;
;![]() или
или
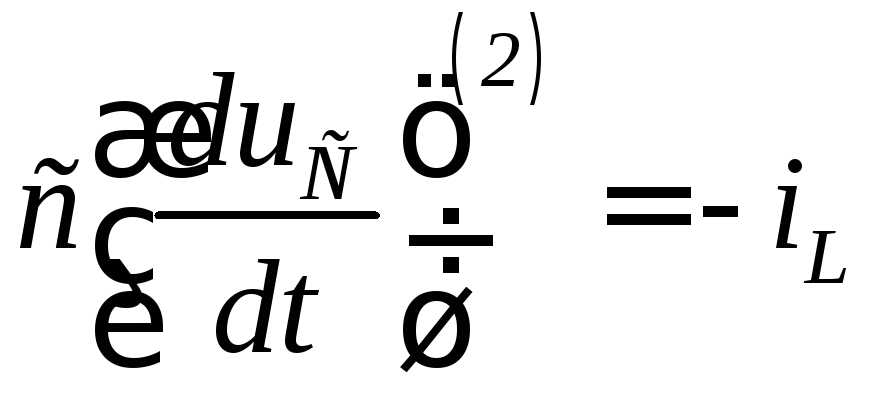 ;
;
 .
.
Отсюда
получаем
![]() ;
;![]() ;
;![]() .
.
Третья частичная схема приведена на рис. 1.71. В ней оставляем только источник ЭДС е(t).
Из
анализа этой схемы вытекает
![]() ;
;![]() ;
;![]() или
или
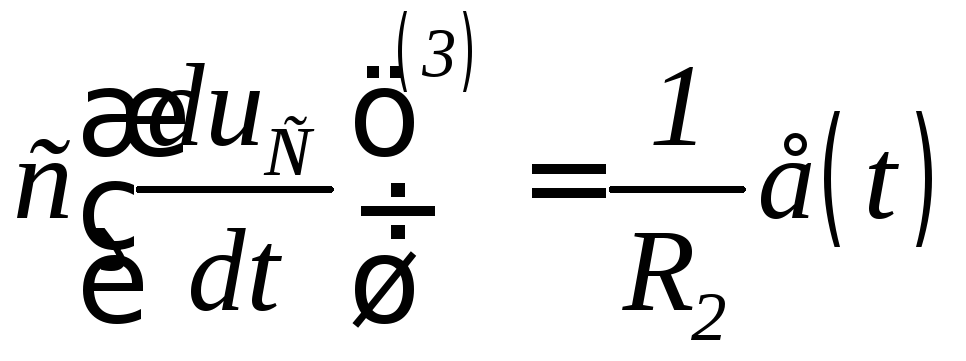 ;
;
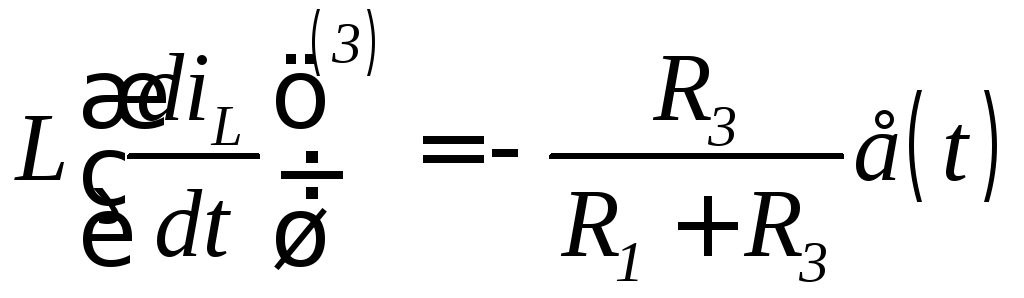 .
.
Отсюда
получаем
![]() ;
;![]() ;
;![]() .
.
Принимая во внимание, что
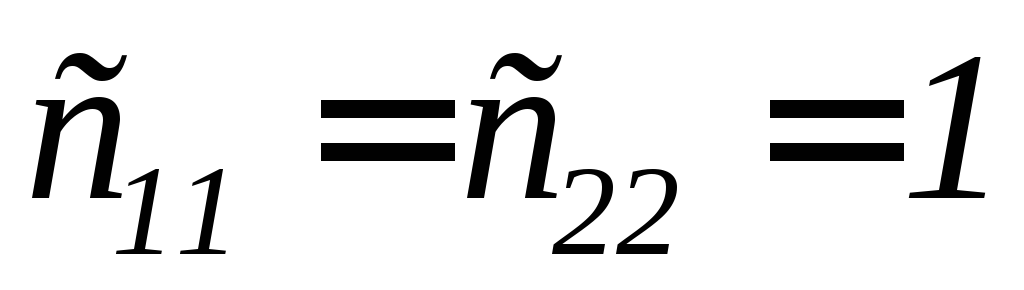 ;
;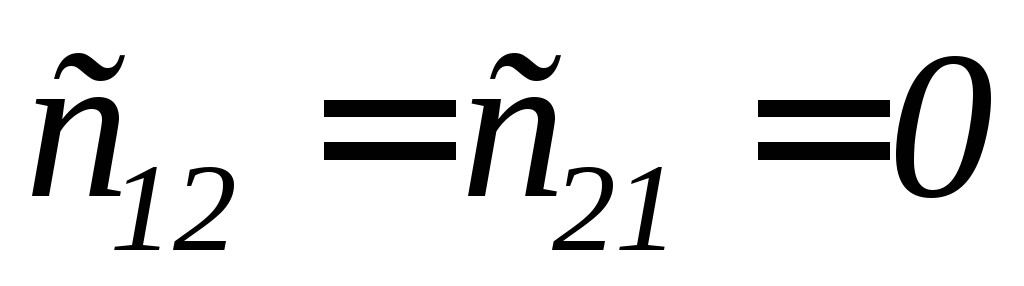 и
и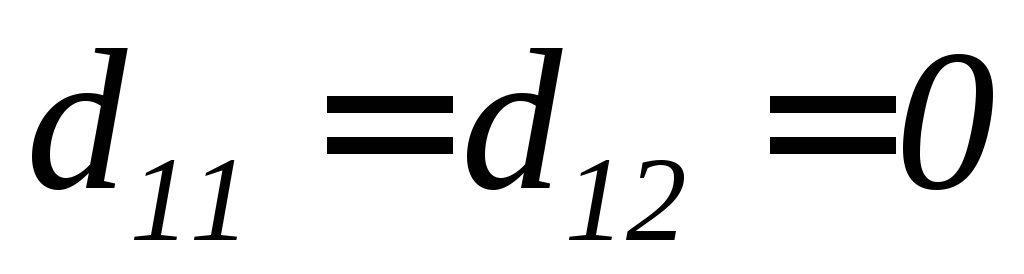 ,
имеем
,
имеем
А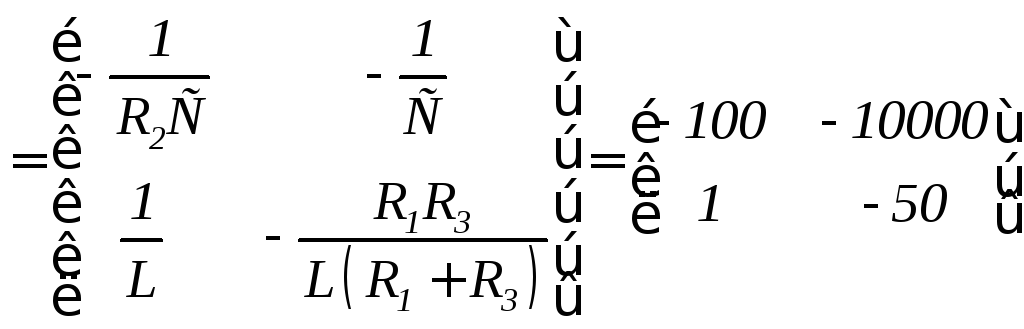 ;
;
В ;
;
С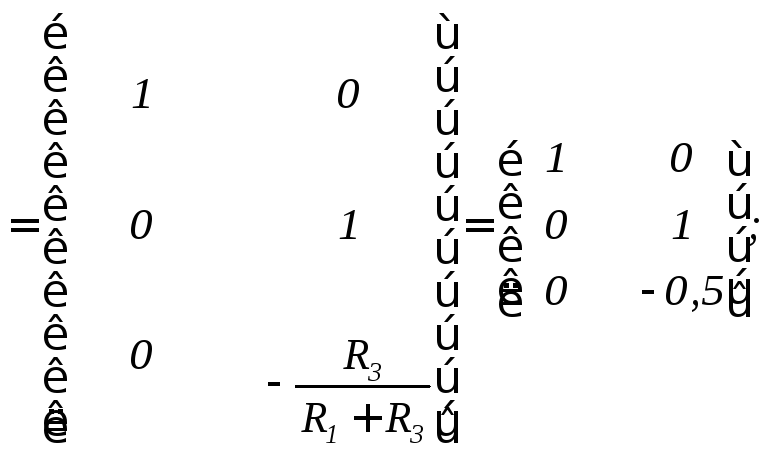
D
Д
 ля
расчета вектораХ(0)
начальных значений переменных состояния
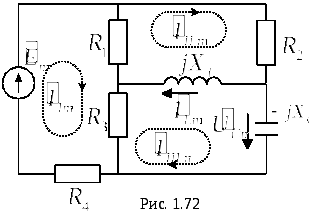
запишем систему уравнений по методу
контурных токов для цепи на рис. 1.72:
ля
расчета вектораХ(0)
начальных значений переменных состояния
запишем систему уравнений по методу
контурных токов для цепи на рис. 1.72:
![]()
![]()
![]()
где
![]()
![]()
![]()
Решая
эту систему, получаем
![]()
![]()
![]() Тогда
Тогда
![]()
![]()
Отсюда
находим
![]()
![]() Таким образом,Х(0)=
Таким образом,Х(0)=![]() .
.
Пример 1.4.
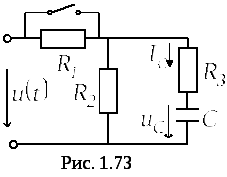 В
цепи на рис. 1.73
В
цепи на рис. 1.73
![]() ;
;![]() ;
;![]() ;С=31,85 мкФ.
;С=31,85 мкФ.
Найти
напряжение
![]() на конденсаторе после замыкания ключа,
если
на конденсаторе после замыкания ключа,
если![]() и
и![]() .
.
Решение
Ищем напряжение на конденсаторе в виде
![]() .
(1.31)
.
(1.31)
2. Для определения принужденной составляющей напряжения рассчитаем комплекс амплитуды этого напряжения в соответствии с соотношением
![]() ,
(1.32)
,
(1.32)
где
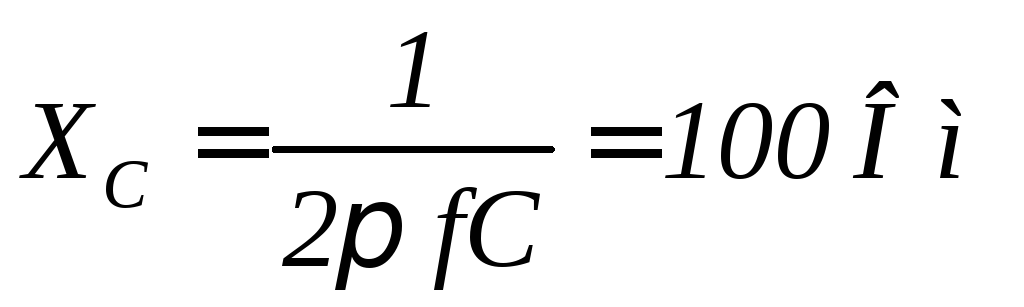 ;
;
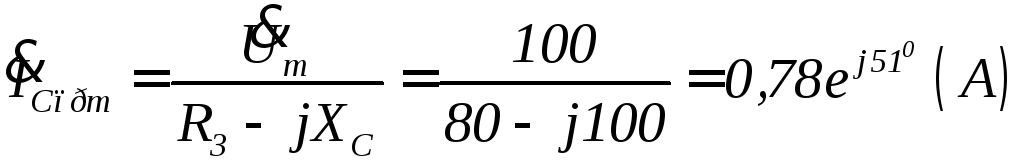 .
.
Отсюда
![]() (1.33)
(1.33)
и
![]() .
.
3. Свободную составляющую напряжения на конденсаторе имеем в виде
![]()
где
![]() .
.
Таким образом,
![]() .
(1.34)
.
(1.34)
4. Подставив (1.33) и (1.34) в (1.32), получим:
![]() .
(1.35)
.
(1.35)
5.
Для определения постоянной интегрирования
запишем (1.35) для
![]() :
:
![]() .
(1.36)
.
(1.36)
В
соответствии со вторым законом коммутации
![]() определяется
в результате расчета цепи на рис. 1.71 до
коммутации. На основании теоремы об
активном двухполюснике для тока в ветви
с конденсатором можно записать:
определяется
в результате расчета цепи на рис. 1.71 до
коммутации. На основании теоремы об
активном двухполюснике для тока в ветви
с конденсатором можно записать:
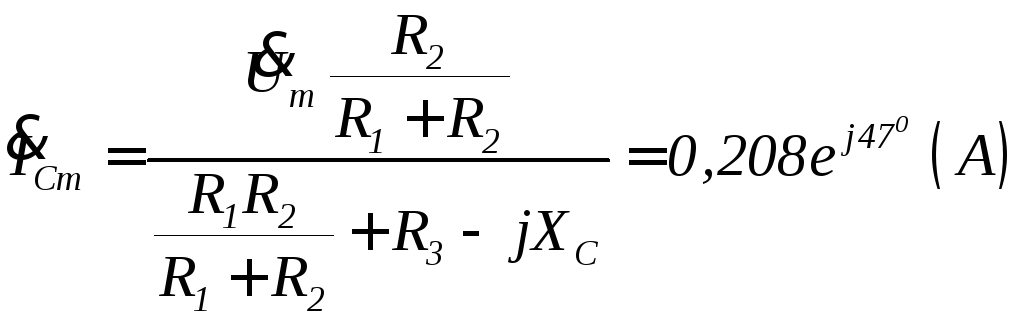 .
.
Отсюда комплексная амплитуда напряжения на конденсаторе до коммутации
![]()
и, следовательно,
![]() .
.
Тогда,
решив с учетом найденного значения
![]() уравнение
(1.36) относительно постоянной интегрирования,
получим
уравнение
(1.36) относительно постоянной интегрирования,
получим
![]() .
.
Таким образом, искомое выражение напряжения на конденсаторе имеет вид
![]() .
.
