
- •Введение.
- •§1. Основные понятия и определения.
- •§2. Дифференциальные уравнения с разделяющимися переменными.
- •§3. Однородные дифференциальные уравнения.
- •§4. Линейные дифференциальные уравнения. Уравнение Бернулли.
- •§ 5. Дифференциальные уравнения второго порядка.
- •§ 6. Частные случаи уравнений второго порядка.
- •§ 7.Линейные дифференциальные уравнения.
- •§ 8 . Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •§ 9. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.
- •Задачи.
Введение.
Методические указания и варианты к типовому расчету по теме «Обыкновенные дифференциальные уравнения» предназначены для студентов факультета ПГС.
Цель данного типового расчета – развитие и закрепление навыков решения задач.
Указания состоят из 9 параграфов. Приводятся краткие теоретические сведения и образцы решения многих типовых задач.
§1. Основные понятия и определения.
Дифференциальным уравнением называется
уравнение, связывающее независимую
переменную x, искомую
функцию![]() и производные этой функции, т.е. уравнение
вида
и производные этой функции, т.е. уравнение
вида
![]() .
.
Если искомая функция
![]() есть функция одной переменнойх, то
дифференциальное уравнение называется
обыкновенным.
есть функция одной переменнойх, то
дифференциальное уравнение называется
обыкновенным.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например:
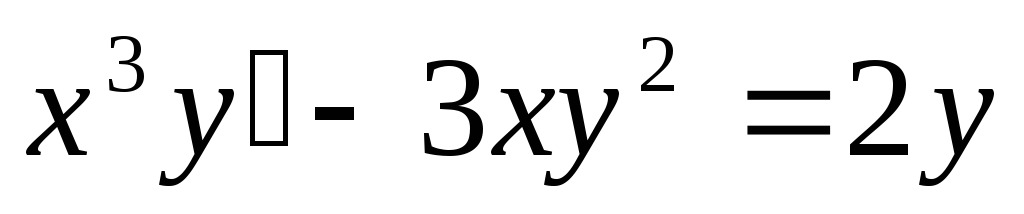 - обыкновенное дифференциальное
уравнение первого порядка.
- обыкновенное дифференциальное
уравнение первого порядка.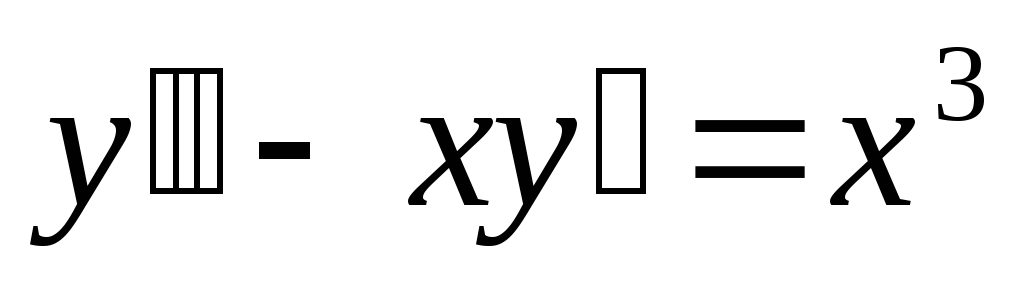 - дифференциальное уравнение второго
порядка.
- дифференциальное уравнение второго
порядка.
Обыкновенное дифференциальное уравнение
первого порядка имеет вид
![]() или
или![]() .
Решением дифференциального уравнения
на интервале
.
Решением дифференциального уравнения
на интервале![]() называется функция
называется функция![]() ,
определенная на интервале
,
определенная на интервале![]() вместе со своими производными, и такая,
что подстановка функции
вместе со своими производными, и такая,
что подстановка функции![]() в дифференциальное уравнение превращает
последнее в тождество поx
на
в дифференциальное уравнение превращает
последнее в тождество поx
на![]()
Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Общим решением дифференциального
уравнения
![]() в областиD называется
функция
в областиD называется
функция![]() ,
обладающая следующими свойствами:
,
обладающая следующими свойствами:
а) эта функция является решением дифференциального уравнения при любом значении произвольной постоянной С, принадлежащей некоторому множеству;
б) для любого начального условия
![]() такого, что
такого, что![]() ,
существует единственное
,
существует единственное![]() ,
при котором решение удовлетворяет
заданному начальному условию.
,
при котором решение удовлетворяет
заданному начальному условию.
Частным решением дифференциального
уравнения![]() называется такое решение
называется такое решение![]() ,
которое получается из общего решения
,
которое получается из общего решения![]() при некотором частном значении
произвольной постояннойС.
при некотором частном значении
произвольной постояннойС.
Задача Коши для дифференциального
уравнения первого порядка
![]() состоит в том, чтобы найти решение,
которое при заданном значении аргумента
состоит в том, чтобы найти решение,
которое при заданном значении аргумента![]() принимает заданное значение
принимает заданное значение![]() ,
т.е. удовлетворяет начальному условию
,
т.е. удовлетворяет начальному условию![]() .
Другими словами, задача Коши состоит в
нахождении частного решения.
.
Другими словами, задача Коши состоит в
нахождении частного решения.
Геометрически задача Коши формулируется
следующим образом: среди всех интегральных
кривых данного дифференциального
уравнения выделить ту, которая проходит
через заданную точку
![]() .
.
§2. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение вида
![]() (1)
(1)
называется уравнением с разделёнными переменными. После интегрирования уравнения (1) его общее решение получается в неявном виде:
![]() ,
,
где F(x) и G(y)– первообразные соответственно для функцийf(x) и g(у), C-произвольная постоянная.
Дифференциальное уравнение вида
![]() (2)
(2)
называется уравнением с разделяющимися
переменными. Делим на
![]() (
(![]() ,
,![]() )
уравнение (2). Получаем
)
уравнение (2). Получаем
![]()
![]()
Интегрируем обе части равенства
![]()
Пример 1.Найти общее решение уравнения.
![]()
Решение.
![]()
![]()
Отсюда имеем
![]()
Предположим, что у≠0. Разделим на у.
![]()
Интегрируя, будем иметь
![]() ,или
,или
![]()
Потенцируя последнее равенство, окончательно получим
у=сх
Пример 2. Проинтегрировать дифференциальное уравнение.
![]()
Найти частное решение, удовлетворяющее условию: у=1 при х=0
Решение: Данное уравнение является
уравнением с разделяющимися переменными.
Разделив обе части уравнения на
произведение
![]() ,
получим уравнение
,
получим уравнение
![]()
Интегрируем.
![]() =0
=0
![]()
![]()
или
![]() .
.
Откуда получаем общее решение
![]() .
.
Чтобы найти искомое частное решение, достаточно определить значение произвольной постоянной по начальным условиям.
1=с(1+0), с=1.
Следовательно, частное решение имеет вид
![]() .
.
Задачи. Найти частное решение.
1.
![]() ;
у=0 при х=0
;
у=0 при х=0
2.
![]() ;
у=5 при х=1
;
у=5 при х=1
3.
![]() ;
у=1 при х=е
;
у=1 при х=е
4.
![]() ;
у=1 при х=0
;
у=1 при х=0
5.
![]() ;
у=1 при х=-1
;
у=1 при х=-1
6.
![]() ;
у=1 при
;
у=1 при![]()
Проинтегрировать дифференциальное уравнение с разделяющимися переменными
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]() =0
=0
