3.2 Расчёт и вычерчивание схемы планетарного редуктора

1. Определим передаточное отношения планетарного редуктора:

2. Исходя из полученного передаточного отношения, выберем схему планетарного редуктора.

Выбираем схему 2К-h(а) () – передача с одновенцовым сателлитом.

3. Расчёт передачи. Подберём количество зубьев и число сателлитов: - Z_a≥ 16 -Z_gподберём по формуле Z_g=Z_a(U_пл-2)/2 -Z_bподберём из условия соосностиZ_b=Za+ 2Z_g- сумма чиселZ_aиZ_bдолжна быть кратна числу сателлитовn_ω; отсюда подберём предположительное число сателлитов. Результаты расчётов представлены в таблице ниже.

Вариант	I	II	III	IV	V
Za	16	17	18	19	20
Zg	36	37	40	43	45
Zb	88	91	98	105	110
Число сателлитов	nω = 4	nω = 3	nω = 4	nω = 4	nω = 5

Выберем подходящий вариант по условию соседства: sin(π/n_ω)>(2+Zg)/(Za+Zg); ВариантI. sin(π/4)>(2+36)/(16+36); 0,707<0,73, не подходит. ВариантII. sin(π/3)>(2+37)/(17+37); 0,866>0,722, подходит. ВариантIII. sin(π/4)>(2+40)/(18+40); 0,707<0,73, не подходит. ВариантIV. sin(π/4)>(2+43)/(19+43); 0,707<0,73, не подходит. ВариантV. sin(π/4)>(2+45)/(20+45); 0,707<0,73, не подходит. По условию соседства подходит только вариантII. Поэтому окончательный ответ:

Z_a= 17

Z_g= 37

Z_b= 91

n_ω= 3

Условия проектирования:

1. Передаточное отношение

Расчётное значениеU_пл= 6,47. Вычислим ошибку: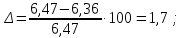

1,7%<2,5%, следовательно такое значение можно принять.

2. Условие соосности: Z_b=Za+ 2Z_g; 91 = 17 + 2 · 37

3. Условие соседства:

sin(π/n_ω)>(2+Zg)/(Za+Zg); sin(π/3)>(2+37)/(17+37); 0,866>0,722

4. Условие сборки: Z_a+Z_b=En_ω, гдеE– любое целое число. 17 + 91 = 36 · 3

4. Рассчитаем КПД планетарного редуктора:

5. Рассчитаем скорость вращения сателлита относительно водила: c^-1 ;

с^-1

6. Передаточное отношение от сателлита к водилу:

7. Рассчитаем диаметры зубчатых колёс: d_a=Z_a ·m= 17 · 2 = 34 ммd_b=Z_b·m= 91 · 2 = 182 ммd_g=Z_g ·m= 37 · 2 = 74 мм

8. Вычертим схему планетарной передачи в соответствии с найденными характеристиками. Схема планетарной передачи вычерчивается в масштабе, причём зубчатые колёса имеют размеры по делительным диаметрам и в соответствии с заданным модулем и найденным числом зубьев.

Рис. 10. Схема планетарной передачи.

Заключение

В процессе курсового проектирования был произведён структурный анализ механизма, в котором была установлена степень подвижности данного механизма W=1, определён класс механизма (II) и составлена формула строения механизма.

Так же в процессе курсового проектирования был произведён кинематический анализ механизма подачи заготовок, в котором была спроектирована схема механизма в 12-ти положениях, построены планы скоростей и ускорений, а так же составлены графики перемещений, скорости, ускорения, мощности и силы сопротивления выходного звена.

Был произведён силовой анализ механизма подачи заготовок, в результате которого двумя способами была определена уравновешивающая сила (P_у = 3507,87 Н), а так же реакции в кинематических парах и другие силы.

Спроектирована цилиндрическая эвольвентная зубчатая передача с числами зубьев на колесах z₁=14 и z₂=27 и модулем m=4. Также спроектирован планетарный редуктор с тремя сателлитами. Числа зубьев колес редуктора:Z_a=17,Z_b=91 иZ_g=37. Спроектированный планетарный редуктор обеспечивает передаточное отношениеU_пл = 6,47.

Зубчатые механизмы привода являются самыми распространёнными в отрасли строительного и дорожного машиностроения. Параметры зубчатых механизмов могут существенно влиять на работоспособность соответствующих машин. Поэтому оптимальный синтез механизмов может дать существенный экономический эффект.

Проектирование позволяет приобрести навыки в анализе и выборе оптимального в данных условиях решения.