2. Силовой расчёт механизма подачи заготовок.

1. Перенесём схему механизма для рабочего хода (положение 3) с 1 листа. На расчётной схеме механизма при рабочем ходе ползуна обозначим все необходимые силы. Будем учитывать силу полезного сопротивления P_пс. Силами тяжести звеньев можно пренебречь.

2. Разложим механизм на структурные группы: механизм состоит из механизма первого класса и двух последовательно присоединённых структурных групп второго класса. Формула строения механизма имеет вид: I_0,1←II_2,3←II_4,5.

Рис. 2. Расчётная схема механизма при рабочем ходе ползуна.

3. Начнём силовой расчёт с последней структурной группы звеньев 4-5. Рисуем её отдельно, а отброшенные звенья заменяем силами и(в точкеD), а в точке С ставим вектор силы полезного сопротивленияP_пси силуR₀₅(рис. 3).

рис. 3. Расчётная схема для структурной группы звеньев 4-5 и звена 4.

Рассмотрим равновесие структурной группы: векторная сумма всех сил должна быть равна нулю и сумма моментов должна быть равна нулю. Запишем первое условие равновесия (количество чёрточек над символам соответствует числу известных параметров):

В этом уравнении три неизвестные: величины трёх реакций,и, а с помощью плана сил можно найти только две неизвестные. Для этого находим одну величинуаналитически, используя известные уравнения статики:

∑М_с=0;

4. Теперь выберем масштаб плана сил μ_p, который находится, как отношение силы полезного сопротивления к величине отрезка на чертеже, соответствующего данной силе.

5. Чертим план сил для структурной группы звеньев 4-5 и звена 4, чтобы найти две оставшиеся реакции и. Откладываем на плане сил все известные силы и проводим направления неизвестных реакций, которые, пересекаясь, ограничивают друг друга (рис. 4).

Рис. 4. План сил для структурной группы звеньев 4-5 и звена 4.

Найдём оставшиеся реакции из плана сил, умножив их длину на масштаб: = 44,98 мм; =>= 44,98 · 26,47 = 1190 Н

= 121,9 мм;=> = 121,9 · 26,47 = 3226,69 Н

6. Рассмотрим структурную группу звеньев 2-3. Рисуем её отдельно, а отброшенные звенья заменяем силами ,,,,и(рис. 5).

Рис. 5. Расчётная схема для структурной группы звеньев 2-3 и звена 2.

Запишем векторное уравнение сил для этой структурной группы: В этом уравнении полностью известна реакция, а остальные известны только по направлению. Таким образом, имеются четыре неизвестных, две из которых – тангенциальные составляющиеи, а две – нормальные составляющиеи- из плана сил. Найдём тангенциальные составляющие аналитически через уравнения статического равновесия:

Для звена 2: ∑М_b= 0;·AB= 0; =>= 0. Для звена 3: ∑М_b= 0;·EB-·h₄₃ = 0;=

7. Строим план сил для структурной группы звеньев 2-3 и звена 2, чтобы найти две оставшиеся реакци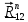и: и. Для этого разделим полученные значения тангенциальной составляющей и силыR₄₃на масштаб плана сил и начертим эти векторы в соответствии с их направлениями, после чего соединим их под прямым углом векторами сил нормальных составляющих (рис. 6):

рис. 6. План сил для структурной группы звеньев 2-3 и звена 2.

Найдём оставшиеся реакции из плана сил, умножив их длину на масштаб: = 60,87 мм; =>= 60,87 · 26,47 = 1611,23 Н

= 133,4 мм;=> = 133,4 · 26,47 = 3531,098 Н

8. Рассмотрим механизм первого класса. Структурная группа имеет степень подвижности W=0 и она статически определима. Механизм 1 класса имеетW= 1 и для статической определимости необходимо приложить к ведущему звену уравновешивающую силуP_y. Физически эту силу может развивать двигатель. Принято считать, что её развивает зубчатая передача, приводящая кривошип в движение. Поскольку нет дополнительных указаний, приложим эту силу к концу кривошипа и перпендикулярно кривошипу, как показано на расчётных схемах ниже:

рис. 7. Расчётная схема для механизма 1 класса и ведущего звена 1.

Из условия ∑М_o= 0 найдём уравновешивающую силуP_y:

∑М_o= 0;P_y · OA – R₂₁ · h₂₁ = 0

9. Построим план сил для ведущего звена 1. Для этого известную нам ранее силу R₂₁разделим на масштаб плана сил и проведём её вектор параллельно положению этой силы (133,4 мм). После чертим вектор уравновешивающего момента, который получаем таким же образом (3507,87/26,47 = 132,53 мм) (рис. 8).

рис. 8. План сил для ведущего звена 1.

Из плана сил найдём реакцию опоры R₀₁.

R₀₁ = 15,22 мм;R₀₁ = 15,22 · 26,47 = 402,87 Н.

10. Найдём величину уравновешивающего момента. Его может передавать приводная муфта, соединяющая двигатель или редуктор с кривошипом. Величину этого момента также, как и в предыдущем случае уравновешивающую силу находят из условия ∑М_o= 0.

∑М_o= 0;

M_y=P_y·𝓁OA= 3507,87 Н · 154,35 мм = 541439,73 Н.

Определение уравновешивающей силы с помощью рычага Жуковского

Решение этой задачи выполним для рабочего хода (3 положение механизма). С первого листа скопируем план скоростей, соответствующий положению рабочего хода механизма и повернём его на 90⁰по часовой стрелке.

На этом плане находим точки, к которым приложены внешние силы, и рисуем эти силы. В нашем случае это точка «С», к которой приложена сила полезного сопротивления P_пси точка «А», к которой приложена уравновешивающая силаPy(рис. 9).

рис. 9. Построение рычага Жуковского.

Далее, рассматривая эту схему как жёсткий рычаг, приравниваем нулю сумму моментов всех сил относительно полюса «P» и вычисляем уравновешивающую силу:

∑М_p= 0;

P_y· (pa) –P_пс· (pc) = 0;

Масштаб плана скоростей равен 52,96 м/с/м; разделим полученное значение на масштаб плана скоростей и получим длину вектораP_yв масштабе: 3523,69/52,96 = 66,53 мм.

Расхождение между методами