МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА 41

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

старший преподаватель				А. В. Сорокин
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ

по дисциплине: МОДЕЛИРОВАНИЕ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	Z9411				Р. С. Кафка
	номер группы		подпись, дата		инициалы, фамилия
Студенческий билет №	2019/3603

Санкт-Петербург 2023

1. Цель работы:

1. ознакомление с возможностями средств Excel и MATLAB по изучению основных законов распределений (ЗР) одномерных случайных величин (СВ);

2. исследование зависимости графиков функций распределения и функций плотности вероятности от параметров распределений;

3. изучение возможностей пакетов Excel и MATLAB по моделированию и анализу одномерных случайных величин.

2. Постановка задачи:

1. Необходимо выполнить следующие задания:

для каждого из следующих трех видов распределений:

• нормального N(9, 3) (σ > 0),

• равномерного R(9, 18) (a < b),

• экспоненциального E(4.5) (λ > 0)

написать программу вывода в графическом окне графиков функций распределения с использованием функций Excel и MATLAB.

2. Написать программу, осуществляющую моделирование массивов объемом 300 для законов распределения: нормального, равномерного, экспоненциального:

• для нормального распределения N(m, σ) (σ> 0):

m=9 σ=√9;

• для равномерного распределения R(a ;b) (a<b):

a=9, b= 18;

• для экспоненциального распределения E(λ)( λ> 0 ):

Для каждого из этих массивов вывести в графическом окне график гистограммы относительных частот группированной выборки (шесть – восемь интервалов группировки). Продемонстрировать полученные результаты преподавателю.

3. Исходные данные по варианту:

Вариант №9

m = 9

σ = 3

a = 9

b = 40

λ = 4.5

4. Основные определения:

Случайная величина – величина, которая при испытаниях принимает одно из возможных

значений, наперед неизвестно какое. Бывают дискретными и непрерывными.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления. Сумма всех вероятностей Σpi = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi)

Функция распределения – функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее или равное х, где х – произвольное действительное число.

Плотностью распределения вероятностей непрерывной случайной величины Х

называется функция f(x) – первая производная от функции распределения F(x). Смысл плотности распределения состоит в том, что она показывает, как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

Коэффициент асимметрии – числовая характеризующая степени несимметричности

распределения данной случайной величины.

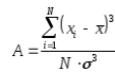
Коэффициент эксцесса (коэффициент островершинности) – мера остроты пика распределения случайной величины.

5. Графики плотности и функции распределения для нормального закона распределения

На рисунке 1 изображен график плотности распределения по нормальному закону.

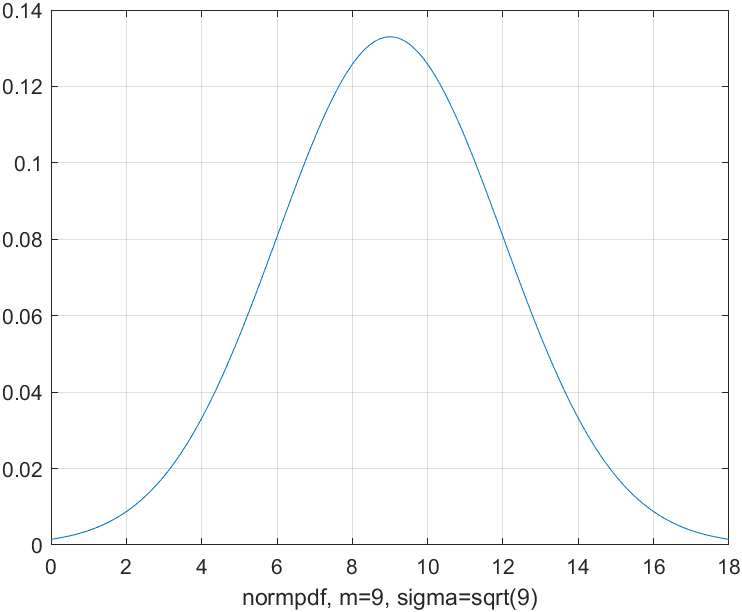
Рисунок 1 - График плотности распределения нормального закона

На рисунке 2 изображен график функции распределения нормального закона.

Рисунок 2 - График функции распределения нормального закона

Листинг программы:

clear all m=9; sigma = sqrt(m); x = m-3*sigma:0.01:m+3*sigma; y_p = normpdf(x,m,sigma); figure (1) plot(x,y_p) grid on xlabel('normpdf, m=9, sigma=sqrt(9)') axis([0 18 0 0.14]); y_F = normcdf(x,m,sigma); figure (2) plot(x,y_F) grid on xlabel('normcdf, m=9, sigma=sqrt(9)') axis([0 18 0 1]);