3.2.2. Поправка Ирвина на пластичность

В окрестности вершины трещины в реальных конструкционных материалах возникает пластическая зона, размеры которой в первую очередь зависят от свойств материала и уровня напряжений. Вместе с тем можно показать, что даже при значительных размерах этой зоны (до 0,2 длины трещины) поле напряжений вблизы пластической зоны достаточно точно определяется асимптотическими соотношениями (3.15). С учётом этого обстоятельства Ирвин (1960) предложил учитывать влияние повышенной податливости в зоне вершины трещины путем введения некоторой поправки на длину трещины.

Полагается, что локальные напряжения вблизи вершины трещины нормального отрыва вдоль осидостигают предела текучестина расстоянии(рис. 3.4). Из соотношений (3.15) имеем

. (3.29)

Далее считается, что в зоне вершины трещины имеет место перераспределение напряжений, при котором условные упругие напряжения в области вершины трещины (при , рис. 3.4 а) обуславливают увеличение области текучести. Радиус этой области(рис. 3.4 б) можно найти из уравнения

. (3.30)

Из уравнений (3.29) и (3.30) получаем

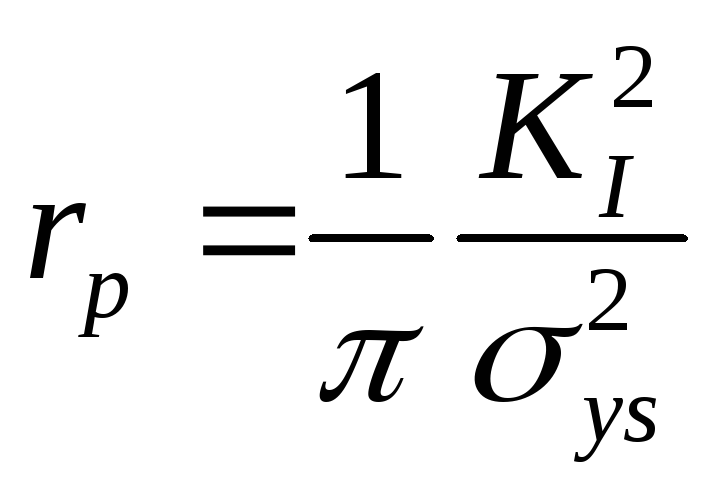. (3.31)

Поправка Ирвина на пластичность в зоне вершины трещины предполагает состоит в увеличении «физической» длин трещины на величину, то есть

, (3.32)

где - расчетная длина трещины при определении.

3.2.3. Энергетические критерии хрупкого разрушения

Представим себе бесконечную пластину с трещиной (рис. 3.3), к которой приложены растягивающие напряжения , величина которых монотонно возрастает. При достижении нагрузки некоторой величины(предельной нагрузки) длина трещины начнёт увеличиваться, вследствие чего пластина разрушится. Гриффитс предложил следующую модель разрушения такого типа:увеличение длины трещины приводит к уменьшению энергии упругих деформаций тела за счёт увеличения его поверхностной энергии, обусловленного образованием новых поверхностей в зоне вершины трещины. В соответствие с предложенным им принципом трещина начинает распространяться, если выполняется следующее условие

, (3.33)

где - работа разрушения, которая требуется для образования новой поверхности, связанной с увеличение длины трещины,- интенсивность освобождающейся упругой энергии, то есть поток энергии в вершину трещины на единицу площади трещины.

Как показывает анализ, затраты энергии на создание новых поверхностей в основном связаны с работой пластической деформации материала, расположенного перед фронтом трещины. Орован (1945) и Ирвин (1948) показали, что если размер пластической зоны мал по сравнению с длиной трещины, то поток энергии можно рассчитать в соответствии с упругим решением, а работу разрушениясчитать работой пластической деформации.

Если при нагружении тела в результате развития трещины точки приложения постоянных внешних сил смещаются, то правая часть уравнения (3.33) представляет собой разность между работой внешних сил и энергией деформации; если точки приложения внешних сил закреплены, то работа внешних сил равна нулю.

В обоих указанных случаях величина равна

, (3.34)

где - потенциальная энергия тела; знак плюс относится к случаю действия постоянной силы, а знак минус – к случаю, когда точки приложения сил фиксированы.

Вычислим величину . Для этого мысленно увеличим длину трещины – математического разреза на некоторую величину(рис. 3.5). Для трещины нормального отрыва на берегах этого разреза действуют напряжения, определяемые соотношениями (3.15). При увеличении длины

трещины на величину его берега перемещаются относительно друг – друга. При этом поток энергииможет быть определён как работа силна перемещениях

. (3.35)

С учётом (3.15), в выражении дляив выражении для, получаем

. (3.36)

Из (3.36) следует, что могут быть предложены два эквивалентных критерия разрушения: энергетический

, (3.37)

где - удельная (эффективная) работа разрушения, и силовой. Величинучасто называют вязкостью разрушения (так же, как и).

Г.П.Черепановым (1968) и независимо от него Дж.Райсом (1968) было показано, что

, (3.38)

где - контур, охватывающий вершину трещины (рис. 3.6); компоненты вектора поверхностных сил, определяемых как ; - - тангенсы углов наклона нормали к осям и; - компоненты тензора деформаций; - компоненты вектора перемещений; - плотность энергии

деформации () не зависит от пути интегрирования, если выполняется одно из условий:

- имеют место упругие (включая нелинейно упругие) деформации;

- имеет место потенциальное поле упруго-пластических деформаций, то есть

. (3.39)

- интеграл характеризует работу разрушения, необходимую для приращения трещины на длину

. (3.40)

Можно показать, что для плоской деформации имеет место соотношение

.

Критерий распространения трещины в терминах - интеграла формулируется следующим образом: трещина начинает расти, когдаJ – интеграл достигает критического значения, постоянного для данного материала

. (3.41)

Для идеально хрупкого разрушения представляет собой поток упругой энергии в вершину трещины, откуда следует, что . Тогда из (3.36) имеем

. (3.42)

Для экспериментального определения величины используется то обстоятельство, что он является производной потенциальной энергии по длине трещины. Таким образом, равен потенциальной энергии, необходимой для страгивания трещины в момент начала её распространения. Строится кривая “нагрузка - перемещение”. Критическое значение J-интеграла для данного материала определяют из соотношения

,

где Q – площадь под кривой “нагрузка-перемещение” для образцов с различными длинами трещин.

Величина может быть найдена на основе обработки диаграммы “нагрузка – перемещение по линии действия силы ”. Записывают диаграммы “ – ” и определяется поглощенная работа (она равна площади под диаграммой). Величина -интеграла определяется на основе соотношений, зависящих от типа нагружения и геометрии образца [2,4,5].