Расчет параметров календарного плана (кп)

Поточный метод организации строительного производства. Основным современным научным методом организации строительного производства является поточный метод, обеспечивающий ритмичность и высокую производительность труда.

Строительным потоком называется один или несколько процессов строительного производства, выполняемые бригадой (несколькими бригадами) рабочих, результатом которого является готовая строительная продукция.

Поточным строительством называют такой метод организации строительства, который обеспечивает планомерный, и ритмичный выпуск готовой строительной продукции на основе непрерывной и равномерной работы бригад (звеньев) неизменного состава, обеспеченных своевременной и комплектной поставкой всеми необходимыми материально-техническими ресурсами.

Для определения особенностей поточного строительства рассмотрим условный пример. Необходимо построить 3 одинаковых дома. Строительство каждого дома требует последовательное выполнение земляных (ЗЗ), монтажных (ММ) и отделочных (ОО) работ. Допустим, что продолжительность каждой работы требует одинакового времени.

При последовательном методе строительства можно предложить два способа организации работ. Первый способ предполагает последовательное строительство домов, а второй последовательное выполнение работ. И в том и в другом случае продолжительность работ максимальна и равна произведению продолжительности возведения дома на их количество (Т=t*n). Интенсивность потребления ресурсов (материалов, рабочих кадров, машин) будет минимальным и равным результату от деления суммы потребных ресурсов на продолжительность строительства (r=R₁*n/T). Отличие способов заключается в том, что в первом случае земляные, монтажные и отделочные работы ведутся в каждом доме без перерывов, но у бригад, выполняющих земляные, монтажные и отделочные работы после завершения работ в доме планируется перерыв, а во втором случае специализированные бригады работают без перерывов, но на стройках домов планируются перерывы. В первом случае период ввода готовой продукции продолжительнее, чем во втором.

При параллельном методе выполнении работ обеспечивается минимальная продолжительность работ, равная продолжительности возведения одного дома (t), интенсивность потребления ресурсов возрастает в n раз. При параллельном методе начало и окончание строительства всех домов происходит одновременно.

При поточном методе, сохраняя преимущества обоих методов и удается избежать их недостатки. Однородные процессы выполняются непрерывно, а разнородные параллельно. Продолжительность строительства будет больше, чем при параллельном, но меньше, чем при последовательном (Тпосл>Тпот>Тпаралл). Интенсивность потребления ресурсов больше, чем при последовательном, но меньше, чем при параллельном (r посл>r пот>r паралл). Период ввода готовой продукции совпадает с продолжительностью для второго случая последовательного метода.

Описанный пример иллюстрирован при помощи следующих графиков.

Классификация потоков осуществляется в зависимости от вида готовой продукции.

Частный поток – это элементарный строительный поток, представляющий собой один или несколько процессов, выполняемых одним коллективом (бригадой звеном). Продукцией могут быть работы по устройству фундамента, кладке стен, штукатурным работам и т.п.

Специализированный поток – состоит из ряда частных потоков, объединенных единой системой фронтов работ и последовательно выполняемых технологий. Продукцией их являются законченные виды работ (подземная часть здания, отделочные работы).

ГРАФИКИ СТРОИТЕЛЬСТВА

Последовательное выполнение работ

№ Дома	Работы	Работы	Работы
1.	ЗЗММОО
2.		ЗЗММОО
3.			ЗЗММОО
	Расход ресурсов
	ХХХХХХ	ХХХХХХ	ХХХХХХ

№ Дома	Работы	Работы	Работы
1.	ЗЗ	ММ	ОО
2.	ЗЗ	ММ	ОО
3.	ЗЗ	ММ	ОО
	Расход ресурсов
	ХХХХХХ	ХХХХХХ	ХХХХХХ

Параллельное Поточное выполнение работ

№ дома	Работы		№ дома	Работы
1.	ЗЗММОО		1.	ЗЗ ММ ОО
2.	ЗЗММОО		2.	ЗЗ ММ ОО
3.	ЗЗММОО		3.	ЗЗ ММ ОО
	Расход Ресурсов			Расход ресурсов
	ХХХХХХ ХХХХХХ ХХХХХХ			ХХ ХХ ХХ ХХ ХХ ХХ ХХ ХХ ХХ

Фронт работ часто носит название захватки. Захватка – это часть здания, объем работ, которой выполняется бригадой (звеном) постоянного состава с определенным ритмом, обеспечивающим поточную организацию строительства.

Частные и специализированные потоки могут иметь различные направления развития, зависящие от объемно-планировочных решений здания. Горизонтальное развитие потока осуществляется при проведении земляных работ, устройстве фундаментов или кровли. Вертикальное направление характерно при монтаже многоэтажных зданий. По наклонной схеме осуществляют кирпичную кладку.

Объектный поток – совокупность специализированных потоков, состав которых обеспечивает выполнение комплекса работ по сооружению соответствующего объекта строительства; продукцией потока является полностью законченное здание (сооружение).

Комплексный поток – состоит из объектных потоков, одновременно занятых строительством отдельных зданий и сооружений, входящих в состав промышленного предприятия или жилого квартала.

Характерными признаками поточного метода планирования являются

• возможность расчленения производственного процесса на отдельные стадии;

• непрерывный производственный процесс во времени и пространстве;

• одновременность выполнения работ на всех стадиях производства.

Основной признак поточного метода – непрерывность и ритмичность достигаются строгой очередностью работы бригад, когда каждая подготавливает фронт работ следующей за ней бригаде, выполняющий другие виды работ, а также соответствующим расчетом параметров потока (ритм, шаг).

На циклограмме потока рассмотрим характеризующие его параметры (рис. 2.4.5).

Рис.2.4.5. Параметры поточной модели.

Ритм (t) – продолжительность работы бригады на частном фронте работ (захватке, участке).

Шаг потока (t_ш)– промежуток времени, через который из потока выпускается готовая продукция.

Период развертывания (τ) – промежуток времени между началом первого и завершающего процессов, т.е. время в течение которого в работу включаются все бригады.

Производственный цикл (Т_з) – время, равное продолжительности от начала работы первого исполнителя работ до завершения работ последним исполнителем.

Период выпуска готовой продукции (Т_пр) – время, равное продолжительности работ завершающей бригады.

Продолжительность потока (Т_общ)– общая продолжительность ритмичного потока.

Число захваток – число частных фронтов работ.

Количество выполняемых процессов в потоке – число видов работ или число специализированных бригад.

Организационное ожидание (t_орг) – искусственно вводимый в план работ на захватке интервал времени, обеспечивающий выполнение условий поточности (непрерывности) работ.

Критическое сближение потоков – такое взаимное расположение потоков на захватке, при котором время окончания работ предыдущего потока и время начала последующего потока равны. Организационное ожидание при этом отсутствует (равно нулю).

При моделировании строительных потоков применяются не только графические модели, но и матричные, позволяющие проводить аналитические расчеты. Матрица (таблица) имеет размерность M*N (число столбцов равно числу работ, а число строк равно числу захваток. Матрица заполнена значениями продолжительности работ t_ij (i – работа, j – захватка)_.

Для удобства расчетов и наглядности пользования матрицей ее представляют в виде сетки с ячейками. Элементом матрицы поточного плана является ячейка, расположенная в столбце работы i выполняемой на захватке j .

	i	i+1
j	tijн tij tijo tijк	ti+1,jн
j+1	ti,j+1н

В центр ячейки вписывается значение величины продолжительности работы (ритм), в левом верхнем углу указывается момент начала работы, а в правом нижнем углу момент окончания работы. Если на j-ой захватке между выполнением работ i и i+1 необходимо организационное ожидание, то его величина записывается около правой границы ячейки матрицы.

Расчеты на матрице учитывают следующие соотношения. Момент окончания работы определяется, как сумма момента начала плюс ее продолжительность

t_ij^к = t_ij^н + t_ij, (2.4.2.)

непрерывность выполнения работы бригадой при переходе с одной захватки на другую определяется равенством значений моментов начала и окончания работ

t_i,j+1^н = t_ij^к, (2.4.3.)

продолжительность ожидания определяется как разность между значениями моментов начала i+1 работы окончания i – ой работы на захватке j.

t_ij^о = t_i+1,j^н – t_ij^к. (2.4.4.)

Проектирование поточного календарного плана строительных работ связано с определением таких параметров плана, которые с учетом рациональной технологии и организации работ обеспечивают строительство объектов в пределах нормативной продолжительности, непрерывную загрузку ресурсов (бригад, машин, механизмов) и непрерывность ведения работ по каждому объекту.

Разработаны следующие принципы и последовательность проектирования потока для возведения однотипных объектов строительства.

• Устанавливаются объекты, подлежащие строительству поточным методом, т.е. близкие между собой по конструкциям, планировке, этажности и технологии.

• Определяются необходимые для выполнения строительные работы, желательно равные или кратные по трудоемкости.

• Устанавливается целесообразная последовательность выполнения работ в процессе возведения объекта.

• Устанавливается последовательность включения в поток строительства отдельных объектов (определение фронтов работ – захваток).

• Закрепляются процессы за определенными бригадами рабочих, которые оснащаются строительными машинами, инструментом и приспособлениями.

• Рассчитывается или задается нормативная продолжительность выполнения каждой работы строительной бригадой на выделенном фронте работ.

Расчет основных показателей (параметров) потока осуществляется исходя из следующих предположений:

• работу на каждой последовательной захватке начинают с интервалом, равным шагом потока;

• на одной захватке может работать только одна бригада;

• размер каждой захватки остается неизменным для всех видов работ, выполняемых на захватках;

• после выполнения всего комплекса работ на одной захватке работы на каждой из последующих захваток заканчиваются не позднее чем через интервал, равный шагу потока.

Особенности расчета плана зависят от характера ритмичности потоков. Различают следующие виды ритмичности потоков:

• ритмичный поток – в котором все его составляющие имеют единый ритм, т.е. одинаковую продолжительность выполнения работ каждой отдельной бригадой на частных фронтах работ;

• разноритмичный поток – в котором составляющие его частные потоки имеют одинаковые ритмы однотипных работ на разных захватках и различные ритмы разнотипных работ на одной захватке;

• неритмичный поток – в котором неодинакова продолжительность выполнения каждой отдельной бригадой работ на частных фронтах.

Рассмотрим построение календарных планов на примерах.

Построим циклограмму ритмичного потока с t_ij = 1, для работ М=3, выполняемых на N=4 захватках (рис.2.4.6.).

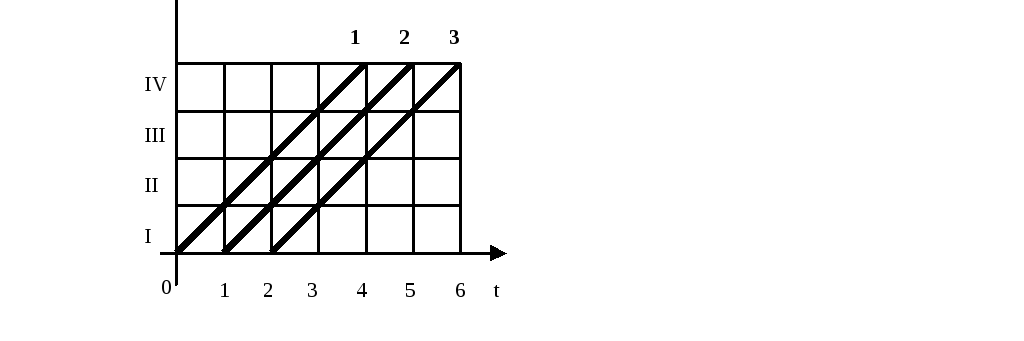
Рис.2.4.6. Циклограмма ритмичных работ.

Первый частный поток на первой захватке начат в момент времени, принятый за 0. Так как ритмы всех работ равны, то линии циклограммы частных потоков имеют вид параллельных прямых. Переход от одной работы к другой на каждой из захваток происходит без ожидания, следовательно всюду имеют место критические сближения потоков. Общая продолжительность потока определяется по моменту завершения последней работы на последней захватке. В рассмотренном примере Т_общ = 6.

Построим календарный план разноритмичного потока, для работ М=4, выполняемых на N=4 захватках. Ритмы работ указаны в матрице, характеризующей данный поток.

Захватки (j)	Работы, бригады (i)
	1	2	3	4
I	2	3	1	2
II	2	3	1	2
III	2	3	1	2
IV	2	3	1	2

Видно, что ритмы для любой из работ на всех захватках одинаковые (2, 3, 1, 2 единицы времени).

Рассмотрим построение циклограммы (рис 2.4.7,а).

Рис. 2.4.7. Циклограмма (а) и линейный график (б) разноритмичного потока.

Сначала проведена линия, описывающая частный поток выполнения 1-ой работы с ритмом, равным 2. В точке завершения 1-ой работы на 1-ой захватке проведена вертикальная штриховая стрелка, указывающая на место критического сближения потоков, и построена циклограмма второго частного потока (ритм равен 3). Анализ графика показывает, что обе работы протекают непрерывно и на каждой захватке в любой момент времени выполняется одна работа. Построим циклограмму 3-ей работы с ритмом равным 1. Рассмотрим линию, проведенную из точки окончания 2-ой работы на 1-ой захватки (штриховая линия). Циклограммы 2 и 3 частных потоков пересекутся в зоне 2-й захватки, что недопустимо, так как это говорит о возникновении коллизии выполнения одновременно двух работ на одной захватке. Чтобы избежать этого частный поток 3-ей работы надо сдвинуть вправо до возникновения критического сближения потоков на последней захватке. В любом другом положении одновременное выполнение двух работ неизбежно. При этом на 1-ой, 2-ой и 3-ей захватках возникают паузы между окончанием 2-ой и началом 3-ей работ (продолжительность пауз показана горизонтальными жирными линиями). Эти паузы носят названия организационных ожиданий. Частный поток 4-ой работы строится также как и 2-ой после критического сближения с 3-ей работой на 1-ой захватке. Никаких нарушений не наблюдается. Можно отметить, что циклограммы выполнения 2-ой и 4-ой работ, имеющих равные ритмы изображаются параллельными линиями.

Проведенное построение позволяет сделать выводы, формулирующие принцип увязки смежных процессов (частных потоков) для разноритмичных потоков. Увязка смежных разноритмичных процессов производится по началу процесса (т.е. по 1-ой захватке), если ритм (продолжительность) t_i+1 последующего процесса больше ритма (продолжительности) t_i данного процесса (t_i+1>t_i). Увязка по концу процесса (по последней захватке) осуществляется, если t_i+1<t_i , т.е. ритм последующей работы меньше предыдущей.

На рис. 2.4.7,б показан соответствующий циклограмме линейный график.

Рассмотрим построение этого же календарного плана матричным методом.

Исходная матрица содержит на пересечении столбцов (работ) и строк (захваток) значения ритмов работ. К матрице можно добавить дополнительную нижнюю строку, в которой указывается значение суммарной продолжительности каждой работы. Это значение указывает увеличивается или уменьшается эта продолжительность относительно продолжительности предыдущей работы. Построение плана начинается с назначения времени начала первой работы на первой захватке. Обычно это время принимается за 0.

Захватки (j)	Работы, бригады (i)
	1			2			3			4
I		2			3			1			2
II		2			3			1			2
III		2			3			1			2
IV		2			3			1			2
Σtij j	8<12 12>4 4<8

Сначала рассматривается первый столбец матрицы и рассчитываются начала и окончания работы на захватках, 1-ый частный поток. При этом используются формулы (1) и (2) из материала предыдущей лекции. Матрица приобретает приведенный ниже вид.

Захватки (j)	Работы, бригады (i)
	1			2			3			4
I	0	2	0 2	2	3			1			2
II	2	2	4		3			1			2
III	4	2	6		3			1			2
IV	6	2	8		3			1			2
Σtij j	8<12 12>4 4<8

Так как задано, что ритм 2-ой работы выше, чем у 1-ой, точка критического сближения потоков должна находиться на первой захватке (1-ой строке). Значение времени начала новой работы равно времени окончания предыдущей работы на захватке с критическим сближением.

t_i+1,j^н = t_ij^к,

После этого последовательно заполняются значениями начала и окончания работ 2-ой столбец матрицы от точки критического сближения до конца столбца. Далее определяется захватка с критическим сближением потоков 2-ой и 3-ей работ и процедура формирования столбца повторяется.

В результате матрица приобретает следующий вид.

Захватки (j)	Работы, бригады (i)
	1			2			3			4
I	0	2	0 2	2	3	6 5	11	1	0 12	12	2	14
II	2	2	1 4	5	3	4 8	12	1	1 13	14	2	16
III	4	2	2 6	8	3	2 11	13	1	2 14	16	2	18
IV	6	2	3 8	11	3	0 14	14	1	3 15	18	2	20
Σtij j	8<12 12>4 4<8

Вматрице в нижнем правом углу выделено значение общей продолжительности работТ_общ = 20. В клетках матрицы указаны значения ожиданий, рассчитанные по формуле (3) из предыдущей лекции.

Построим календарный план неритмичного потока. Необходимо отметить, что неритмичный поток является самым распространенным случаем на практике. Можно предположить, что ритмичный поток может встретиться при строительстве нескольких одинаковых сооружений, когда ритмы работ чудесным образом совпадают, что ожидать на практике сложно. Разноритмичный поток более реален. Он может соответствовать строительству нескольких одинаковых сооружений, когда ритмы работ, естественно, разные. Сохранение ритма на захватках весьма реально, если захватки имеют одинаковый объем работ. Неритмичный поток отражает реальную задачу, когда и объемы работ на захватках и производительность труда для разных работ отличны друг от друга и независимы.

Рассмотрим пример построения плана матричным методом. Построим календарный план для М=4 работ, выполняемых на N=4 захватках. Ритмы работ указаны в матрице, характеризующей данный поток.

Захватки (j)	Работы, бригады (i)
	1			2			3			4
I		3			1			1			1
II		2			2			2			1
III		1			2			4			3
IV		1			2			2			2
Σtij j	7			7			9			7

Как и в случае разноритмичных потоков, сначала рассматривается первый столбец матрицы (1-ый частный поток) и рассчитываются начала и окончания работы на захватках. При этом используются те же формулы (1) и (2) из материала предыдущей лекции.

Для перехода ко второму столбцу матрицы (2-ому частному потоку) необходимо найти точку критического сближения потоков. Эта точка определяется следующим образом. По приведенной ниже формуле рассчитывается ряд из N чисел. Для каждой захватки

Суммируются последовательно значения продолжительности работ первого столбца по номер индекса k (номера захватки) включительно с значениями продолжительности работ второго столбца, начиная с захватки с номером индекса k. В ряд слагаемых для захватки с номером индекса k входят как значение из первого столбца, так и значение из второго столбца матрицы.

S₁=t₁₁+t₂₁+t₂₂+t₂₃+t₂₄=3+1+2+2+2=10;

S₂=t₁₁+t₁₂+t₂₂+t₂₃+t₂₄=3+2+2+2+2=11;

S₃=t₁₁+t₁₂+t₁₃+t₂₃+t₂₄=3+2+1+2+2=10;

S₄=t₁₁+t₁₂+t₁₃+t₁₄+t₂₄=3+2+1+1+2=9.

Среди значений полученного ряда чисел выбирается максимальное значение (S₂=11). На захватке, соответствующей максимальному значению S_k , произойдет критическое сближение потоков. Следовательно, время ожидания принимается равным нулю, время начала следующей работы на этой захватке будет равно времени окончания предыдущей работы.

t_i+1,j^н = t_i,j^к,

	Работы, бригады (i)
	1			2			3			4
I	0	3	1 3	4	1	1 5	6	1	4 7	11	1	12
II	3	2	0 5	5	2	0 7	7	2	3 9	12	1	13
III	5	1	1 6	7	2	0 9	9	4	0 13	13	3	16
IV	6	1	2 7	9	2	2 11	13	2	1 15	16	2	18
Σtij j	7			7			9			7
Sk	10 11 10 9			10 11 11 9			8 9 12 11

После чего расчет может быть продолжен для следующего столбца матрицы. Причем, при увеличении номера захватки (движение вниз по строкам, j+1, j=k) порядок расчета аналогичен рассмотренному выше, а при уменьшении номера захватки (движение вверх по строкам, j-1, j=k)

t_i+1,j-1^к = t_{i+1 j}^н, t_i+1,j-1^н = t_i+1,j-1^к - t_i+1,j-1. (2.4.5.)

Завершив расчет всех значений начал и окончаний работ по второму столбцу матрицы, можно приступить к определению захватки, на которой происходит критическое сближение 2-го и 3-его потоков (работ). Используется тот же, выше рассмотренный алгоритм. Рассчитанный вспомогательный ряд чисел 10, 11, 11, 9 имеет максимальное значение члена ряда равное 11, соответствующее 2-ой и 3-ей захваткам. Для дальнейшего расчета можно выбрать любую захватку. Результат расчета будет аналогичным. Обычно расчет начинают с точки критического сближения на захватке с меньшим номером.

Р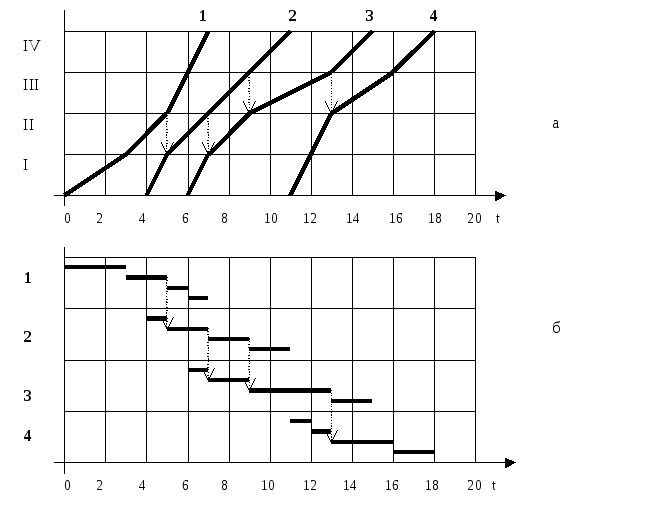ис. 2.4.8. Циклограмма (а) и линейный график (б) неритмичного потока.

Проведя аналогичные расчеты для всех столбцов матрицы (потоков, работ), получают искомый календарный план.

В матрице в нижнем правом углу выделено значение общей продолжительности работ Т_общ = 18. В клетках матрицы указаны значения ожиданий, рассчитанные по формуле (3) из предыдущей лекции.

На рис. 2.4.8,а и 2.4.8,б показаны соответствующие матрице циклограмма и линейный график.

Сетевое моделирование при строительстве объектов и сооружений. Сетевое планирование и управление – это система управления крупными научно-техническими разработками, в том числе строительством, использующая сетевую модель, как форму представления об управляемом объекте.

Сетевая модель – информационная модель комплекса взаимоувязанных работ, заданная в виде сети, отображающей упорядочение работ во времени. Сетевая модель может также содержать и другие характеристики (ресурсы, стоимость и пр.), относящиеся к отдельным работам и комплексу работ в целом.

Сеть комплекса работ рассматривается, как ориентированный конечный граф и отображает отношение предшествования между работами, которым можно представить в соответствие дуги или вершины графа. Наиболее распространено графическое представление модели на плоскости – сетевой график. Возможно представление сетевой модели в виде таблиц.

Целью систем сетевого планирования и управления является разработка оптимального или достаточно близкого к нему варианта строительства, обеспечивающего рациональную увязку во времени выполнения работ и наилучшее использование ресурсов. В результате применения систем сетевого планирования и управления сокращаются сроки строительства, снижается трудоемкость и себестоимость работ.

Основными исходными понятиями сетевого моделирования являются: Работа и Событие.

Работа – любой производственный процесс, требующий затрат времени, материальных ресурсов и приводящий к достижению определенных результатов.

Событие – а) совокупность условий, позволяющих начать работу; б) завершение деятельности (работы), отражающее состояние производства в процессе комплекса работ.

Табл. 2.4.9. Сетевые модели классифицируются по ряду признаков:

Принцип классификации	Классификационные группировки
По характеру отображения связей в графе	Работы – События (Работы – дуги графа)
	События – Работы (Альтернативные сети)
По форме отображения модели	Графические
	Табличные
По количеству независимых целей (количеству целевых событий)	Одноцелевые
	Многоцелевые
	Обобщенные
По степени определенности параметров модели	Детерминированные
	Вероятностные (стахостические)
По составу параметров	С учетом времени
	С учетом времени и ресурсов

Рассмотрим правила построения детерминированного одноцелевого графа, ориентированного на работы. Схематическое изображение всех событий и работ, отражающее их взаимосвязи, носит название топологии сети.

Предлагается рассмотреть 16 правил – примеров.

Первые 8 правил поясняют порядок изображения работ и событий, соединений их между собою и присвоения им кодовых номеров.

Правила 9, 10 и 11 уточняют порядок построения сложных графов.

Правило 12 определяет порядок построения одноцелевого графа.

Правило 13 рассматривает вложенные графы.

Правила 14, 15 и 16 рассматривают процедуры использования фиктивных работ.

Р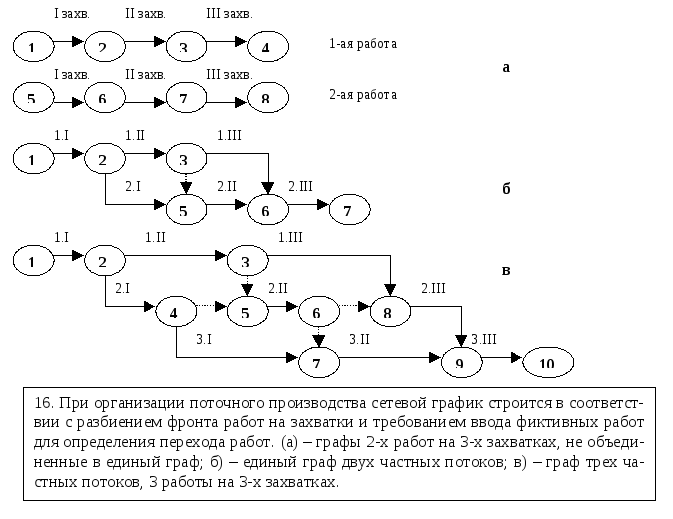ассмотрим пример построения сетевой модели комплекса взаимосвязанных работ. Сначала необходимо задать последовательность выполнения работ. Последовательность может быть задана в виде таблицы.

Имя работы	Имена предшествующих работ	Имя работы	Имена предшествующих работ	Имя работы	Имена предшествующих работ
А	-	Д	Б	И	Д
Б	-	Е	В, Г	К	Д
В	А, Б	Ж	В, Г	Л	И
Г	Б	З	Е. Ж	М	К

Прочерк в таблице обозначает, что соответствующие работы не имеют предшествующих, т.е. являются начальными.

Сначала построим верхнюю схему рис. 2.4.9., которая является предварительной и сугубо вспомогательной. На ней изображены все работы и овалами соединены окончания и начала связанных между собой работ. В этих местах будут впоследствии образованы события. Начала работ А и Б соединены, чтобы образовать одно начальное событие, в противном случае образуется в графе хвост. Окончания работ З, Л и М также объедены для создания завершающего события, в противном случае будут образованы тупики.

После построения предварительной схемы можно ее преобразовать в граф сетевой модели, события в котором прономерованы. Граф изображен под предварительной схемой. В граф введены две фиктивные работы. Работа 12 необходима, чтобы определить порядок выполнения работ В и Г, Д. Работа В (24) выполняется после работ А (12) и Б (13), а работы Г (34) и Д (37) только после Б (13). Направление вектора фиктивной работы показывает, что начальное событие работ Г и Д не связано с конечным событием работы А. Вторая фиктивная работа 56 введена, чтобы разделить конечные события параллельно выполняемых работ Е (46) и Ж (45).

Рис. 2.4.9. Пример построения графа сетевой модели.

Введем следующие обозначения, которые будут использоваться в дальнейшем:

i - номер начального события;

j - номер завершающего события

c_ij – работа, выполняемая между событиями ij, иногда буква «с» отсутствует, тогда просто – ij;

t_ij - продолжительность выполнения работы ij;

l_ij - элемент последовательной цепочки векторов между событиями i и j ;

g_ij - расход ресурсов, необходимых для выполнения работы ij.

Путь – это цепочка работ между двумя событиями. Он может быть описан перечнем номеров, входящих в него событий.

Если рассмотреть некое промежуточное событие сетевого графа, то можно выделить предшествующие пути, от начального события к анализируемому и последующие пути от анализируемого до завершающего или конечного события.

В графе, приведенном в качестве примера на рис. 2.4.10., где в качестве промежуточного события выбрано событие 5:

Предшествующие пути (l₁₅): 1, 2, 4, 5 и 1, 3, 5.

Последующие пути: (l₅₈) 5, 6. 8 и 5, 7, 8.

Полным путем называют набор из всех путей от начального к конечному событию. В рассматриваемом примере его составит набор из 5 путей (l₁₈):

1, 2, 4, 5, 6, 8; 1, 2, 4, 5, 7, 8; 1, 3, 5, 6, 8; 1, 3, 5, 7, 8; 1, 3, 7, 8.

Рис. 2.4.10. Пример для анализа путей в сетевом графе.

Продолжительность пути (Т_ij)– сумма продолжительностей всех работ, принадлежащих данному пути.

Т_ij=Σt_ij

Если рассмотреть полный путь сетевого графа, то продолжительности, входящих в него путей, естественно, будут различны. Путь, продолжительность которого будет максимальна, носит название критического пути (Т_кр). Продолжительность критического пути определяет общую продолжительность выполнения всех работ сетевого графа.

Т_кр = max [Т_ij]

Рассмотрим следующую модель (рис. 2.4.11.).

Рис. 2.4.11. Пример сетевого графа. Вверху – векторная безмасштабная форма, внизу – изображение графа в масштабе времени, работы установлены в положение ранних начал.

Над каждым вектором графа указано число, которое соответствует продолжительности соответствующей работы в некоторых принятых для данного графа единицах времени (часах, сменах, рабочих днях и т.д.).

Пути	Продолжительности путей	Критический путь
1, 2, 4, 6	5 + 4 + 4 = 13
1, 3, 4, 6	4 + 7 + 4 = 15	max [13, 15, 10] = 15
1, 3, 5, 6	4 + 4 + 2 = 10

Ниже рассмотренного графа, построенного в обычной графической форме без масштаба, изображен тот же граф, построенный в масштабе времени.

Граф изображен в соответствии со следующими правилами. Построена горизонтальная ось времени t, вдоль которой указаны отцифрованные значения шкалы времени. Вдоль оси откладываются векторы работ критического пути. Центры окружностей, изображающих события, размещаются в точках, соответствующих отметкам времени оси. Таким образом, продолжительность работ соответствует расстоянию между центрами окружностей событий, а не длине стрелок графа. Параллельно критическому пути изображаются остальные пути графа. Параллельный путь соединяется с событиями критического пути вспомогательными вертикальными линиями, которые тоньше линий векторов. Так как выполнение работ параллельных путей обычно занимает меньше времени, чем связанные с ними отрезки критического пути, то на параллельных путях образуются отрезки времени, которые носят названия резервов времени. Правила изображения работ, имеющих резервы времени следующие. Между двумя событиями проводится вектор, состоящий из двух отрезков, горизонтального и вертикального. Около конечного события располагается стрелка вектора. Горизонтальная линия вектора имеет две разные толщины. Линия вектора имеет толщину, принятую для изображения работ, на длине, соответствующей продолжительности работы. Остальная часть вектора, соответствующая резерву времени, имеет толщину вспомогательных линий. Так как резервы времени могут использоваться после исполнения работы или до исполнения работы, то тонкая часть вектора, т.е. изображение резерва времени, может соответственно менять свое положение. На изображенном графе все работы сдвинуты влево, а резервы используются после выполнения работ. Такое положение работ называют ранним. Противоположное выполнение работ называют поздним. Рис. 2.4.12.

Рис. 2.4.12. Пример сетевого графа. Изображение графа в масштабе времени, работы установлены в положение поздних начал.

Если на таком графе необходимо изобразить фиктивные работы, то они изображаются штриховой линией перпендикулярной к оси времени. Так как продолжительность фиктивной работы равна нулю, то и проекция ее на ось времени должна быль точкой.

Построение плана работ на основании сетевой модели заключается в определении для каждой работы моментов ее начала t_ij^н и окончания t_ij^к.

Планирование должно учитывать следующую систему ограничений.

1. Отношение предшествования работ. Момент начала выполнения работы ij по величине равен или больше значения окончания предшествующей работы mi, т.е. работа начинается в момент окончания предыдущей работы или позже (Рис. 2.4.13., схема а).

t_ij^н t_mi^к . (2.4.6.)

2. Ограничение продолжительности работ. Значение момента окончания работы равен или больше суммы значения момента начала работы и продолжительности работы.

t_ij^к t_ij^н + t_ij (2.4.7.)

3. Ограничение начального момента. Значение момента начала выполнения каждой работы равен или больше значения общего начального момента выполнения плана. Обычно значение этого момента Т_нач принимается равным нулю или задается особо.

t_ij^н Т_нач (2.4.8.)

4. Ограничение директивного срока. Значение момента окончания каждой из работ должен быть равен или меньше значения заданного директивного срока Т_дир.

t_ij^к Т_дир. (2.4.9.)

Как мы увидели при построении графа, привязанного к масштабу времени, некоторые работы, которые не лежат на критическом пути, могут иметь разные значения начала и окончания работ, поэтому вводятся понятия раннего начала t_ij^рн, позднего начала t_ij^пн, раннего окончания t_ij^рк и позднего окончания t_ij^пк для каждой работы.

Ранний срок – минимальный из возможных значений начала (окончания) работы при заданных продолжительностях работ и заданном начальном моменте.

Поздний срок – максимальный из допустимых значений моментов начала (окончания) данной работы, при котором возможно выполнение всех последующих работ с соблюдением директивного срока завершения работ. (Рис. 2.4.13, схема б.)

Рассмотрим формулы для расчета этих четырех показателей.