книги из ГПНТБ / Болдырев, А. И. Физическая и коллоидная химия учеб. пособие

Интенсивность рассеяния света зависит от концентрации коллоидных частиц, от их размеров и формы.

Поскольку разрешающая сила ультрамикроскопа невелика (не пре­ вышает таковую обычных микроскопов, имеющих увеличение в 300— 500 раз), то ни размеры, ни форма частиц в ультрамикроскоп непосред­ ственно не различимы. И все же с помощью ультрамикроскопа мож­ но косвенно судить о размерах и форме коллоидных частиц.

Размеры частиц можно определить приближенно путем следующе­ го расчета.

При помощи микрометрической окулярной шкалы ультрамикроско­ па выделяют определенный объем золя, в котором визуально подсчи­ тывают число находящихся в нем коллоидных частиц. Зная общую мас-

су диспергированного вещества и вычислив количество частиц во всем объеме, можно рассчитать массу одной частицы, и уже по ней, учи­ тывая плотность диспергированного вещества, определить объем и размеры частицы. Пусть d — плотность частиц, С — весовая концен­ трация коллоидного раствора, V — выделенный оптический объем, v — число частиц в объеме V, тогда число частиц п в единице объема будет равно:

Соответственно этому вес отдельной частицы т и ее объем w будут равны:

С

т= — (IX,3)

п

Принимая форму частицы за куб или сферу, можно вычислить размер коллоидной частицы по следующим формулам:

— 380 —

Электронный микроскоп. В последние годы электронный микроскоп нашел самое широкое применение при изучении коллоидных растворов. С его помощью был полностью решен вопрос о форме коллоидных частиц и макромолекул.

Разрешающая способность лучших электронных микроскопов отечественных марок достигает 10—15 А, полное увеличение превышает 600 тысяч. С помощью электронного микроскопа были изучены размеры и форма многих лиофобных кол­ лоидов, аэрозолей, молекул различных высокомолекулярных соединений, виру­ сов. На рис. 158 представлены полученные в электронном микроскопе снимки коллоидных частиц различной формы. Масштаб, указанный на этих снимках, позволяет судить и о размерах частиц.

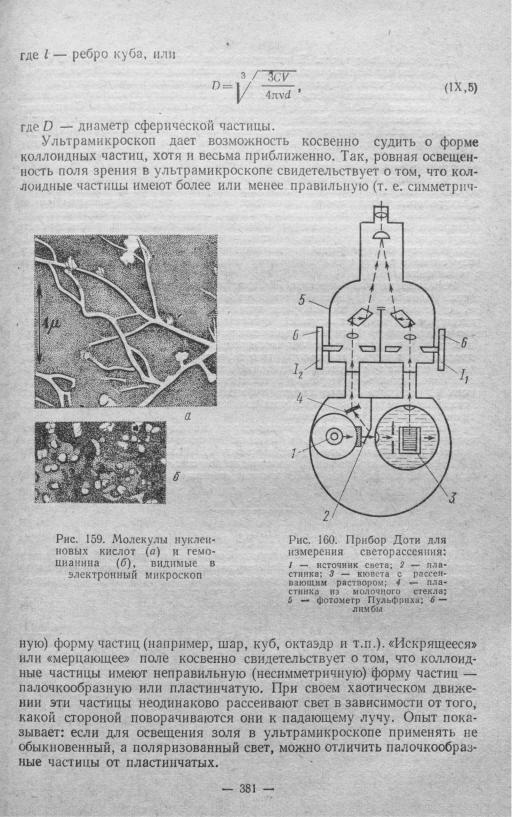
Возможность использования электронного микроскопа ограничена до неко­ торой степени необходимостью тщательно высушивать объект, так как внутри электронного микроскопа поддерживается высокий вакуум. Изучаемые образцы должны быть чрезвычайно тонкими (1—10 мк), поскольку они сильно поглощают электроны. В настоящее время разработаны методы наблюдения в электронном микроскопе не самих образцов, а отпечатков с них (так называемых реплик), которые могут быть получены и с влажных объектов. На рис. 159 представлены полученные в электронном микроскопе снимки молекул нуклеиновых кислот и гёмоцианина.

Нефелометры и нефелометрия. На явлении опалесценции и закона светорас­ сеяния Рэлея основано действие весьма важного оптического прибора нефеломет­ ра, с помощью которого измеряют интенсивность опалесценции коллоидного раствора, а также степень мутности суспензии или эмульсии. На рис. 160 пока­ зана схема прибора Доти, предназначенного для визуального измерения свето­ рассеяния. В этом приборе свет от источника 1 падает на рассеивающий раствор, находящийся в термостатированной кювете, и пластинкой 2 частично направля­ ется на пластинку из молочного стекла 4, которая является стандартом «мутно­ сти». Интенсивность стандартного пучка от пластинки 4 и света, рассеянного под углом 90° в кювете 3, сравнивается в фотометре Пульфриха 5 и уравнивается с помощью лимбов 6. Отсчеты на этих лимбах Д и /2 характеризуют отношение интенсивностей рассеянного света.

В настоящее время широкое распространение получили так называемые фо­

Нефелометры применяются для определения степени дисперсности (размера частиц) коллоидных растворов. Этот метод основан на уравнении:

Л__о |_ _ £ ?

(IX,6)

h ~ D f ~ rl

которое легко выводится из уравнения Рэлея (IX, 1) при постоянстве значений /0 и А. для одного и того же золя с одинаковой весовой концентрацией, но с разной степенью дисперсности его частиц. Оно показывает, что интенсивность рассеяния, а следовательно, и интенсивность опалесценции и свечения конуса Фарадея — Тиндаля прямо пропорциональны кубу радиуса (размера) тчастицы или обратно

Для этого метода необходимо иметь стандартный раствор (золь или суспензию) того же вещества с монодисперсными частицами, радиус которых точно известен. Это условие до некоторой степени ограничивает данный метод.

С помощью нефелометрии можно легко определить концентрацию золя. Формула для определения концентрации золя может быть легко выведена из уравнения Рэлея;

— 382 —

Для двух золен одного и того же вещества, обладающих одинаковой степенью

где С4 — искомая весовая концентрация, равная (Vjl^d.

Таким образом, для определения концентрации золя нефелометрическим спо­ собом необходимо иметь стандартный раствор с известной концентрацией С того же вещества, что и объект исследования.

§ 109. Молекулярно-кинетические свойства коллоидных растворов

Как показали многочисленные исследования, коллоидные сис­ темы по своим молекулярно-кинетическим свойствам принципиально ничем не отличаются от обычных (истинных) растворов, только эти свойства у золей и растворов высокомолекулярных соединений выра­ жены значительно (в сотни и тысячи раз) слабее.

Все другие молекулярно-кинетические свойства основаны на броу­ новском движении.

Броуновское движение. Частицы дисперсной фазы золя под влиянием ударов молекул растворителя находятся в состоянии непре­ рывного хаотического движения. Так, если рассматривать какой-либо

колебательные движения (в виде своеобразного, никогда не прекра­ щающегося «танца»), совершаемые растительной пыльцой при рас­ сматривании ее суспензии в воде в микроскоп. Вначале Броун считал, что эти движения присущи только живым существам, но вскоре убедил­ ся, что они свойственны любым суспензиям и эмульсиям органических и неорганических веществ при условии, что размер частиц достаточно мал (в пределах от 1 до 5 мк). Было предложено много различных ги­ потез для объяснения броуновского движения, но все они оказались несостоятельными.

Позднее Г у и (1888) и Э к с н е р (1900) высказали мысль о том, что броуновское движение имеет молекулярно-кинетическую природу, т. е. является следствием теплового движения. Это было впоследствии

и С в е д б е р г а .

Опыты показали, что броуновское движение совершенно не зави­ сит от природы вещества, оно изменяется в зависимости от температуры,

—383

вязкости среды и размеров частиц. Под действием беспорядочных уда­ ров молекул растворителя частицы дисперсной фазы также совершают беспорядочные движения. Перемещение в пространстве этих частиц совершается в результате усредненного действия всей совокупности ударов за время наблюдения (в 1 сек частица испытывает около Ю20 уда­ ров). Число ударов, приходящихся с разных сторон, при малых раз­

мерах частиц обычно неодинаково и они передвигаются в пространстве по сложной траектории (рис. 161). Если размеры и масса частиц дисперсной фазы превышают определенные пре­ делы, вероятность взаимной компен­ сации ударов оказывается значитель­ но выше. Вот почему частицы разме­ ром, например, 4—5 мк совершают только небольшие колебательные дви­ жения около некоторого центра. При более крупных размерах частиц броу­ новское движение прекращается во­ все.

нить свое направление, а человеческий глаз способен улавливать не более 10 движений в секунду и притом лишь в крупном масштабе. Это заставило в теорию броуновского движения вместо средней квадра­ тичной скорости для газовых молекул ввести несколько иное понятие —

среднее квадратичное смещение, или средний сдвиг ± Дх, как проекцию расстояния между двумя положениями частицы А и В за время t двух смежных наблюдений (рис. 161). Зависимость среднего смещения части­

цы Ах за время t от коэффициента диффузии D выражена Эйнштейном в виде уравнения:

Коэффициент диффузии для сферических частиц, значительно больших

— 384

по размерам, чем молекулы дисперсионной среды, выражается еледующим уравнением:

Уравнения (IX ,11) и (IX,12) имеют очень большое значение в кол­ лоидной химии, так как позволяют на основании измерений коэффици­ ента диффузии D определить радиус взвешенных коллоидных частиц сферической формы, а также величину молекул высокомолекулярных соединений. Для частиц или макромолекул несферической формы выражение блту в уравнении (IX ,12) заменяется более сложным.

Подставляя в уравнение (IX ,11) значение D из уравнения (IX,12), для среднего сдвига частицы получим:

Изучение броуновского движения позволило Перрену при содей­ ствии математика Ланжевена впервые экспериментально путем непо­ средственного подсчета в поле зрения ультрамикроскопа определить одну из наиболее важных констант — число Авогадро N0. Найденное им значение этого числа N0 = 6,5 • 1028 хорошо согласуется с дру­ гими известными данными.

Таким образом, изучение броуновского движения (наряду с уль­ трамикроскопией) имело большое значение не только для коллоидной химии, но и для всего естествознания в целом как одно из доказательств справедливости диалектико-материалистической концепции миропо­ нимания.

Диффузия и флуктуация. Вследствие молекулярно-кинетического движения частицы дисперсной фазы испытывают случайные смещения, например, вверх и вниз. Однако если в каком-либо растворе частицы распределены неравномерно (содержание их у дна сосуда больше, чем в верхцем слое), общее число смещений частиц снизу вверх будет боль­ ше, чем сверху вниз. При этом частицы будут передвигаться вверх до тех пор, пока не наступит выравнивание концентраций.

Самопроизвольный процесс выравнивания концентраций ионов, молекул или-коллоидно-дисперсных частиц за счет их беспорядочного теплового движения (у коллоидных частиц — броуновского движения) получил название диффузии. Диффузия как самопроизвольный про­ цесс для всех дисперсных систем подчиняется одним и тем же законо­ мерностям, установленным Фиком для газов. Согласно первому за­ кону Фика скорость диффузии прямо пропорциональна плоищди, через которую происходит диффузия, и градиенту концентрации. Мате­ матически этот закон имеет следующее выражение:

dm

(IX, И)

It

где dm — масса вещества (в молях или граммах), продиффундировавшая за бесконечно малое время dt через площадь S; dC(dx — падение

концентрации на бесконечно малом отрезке диффузионного пути dx, называемое градиентом концентрации; D — коэффициент диффузии, индивидуально характеризующий диффузионную способность данной дисперсной системы. Этот коэффициент выражает количество веще­ ства, диффундирующего в единицу времени (1 сек) через единицу пло­ щади (1 см2) при градиенте концентрации, равном единице.

С изменением концентрации в процессе диффузии величина гра­ диента концентрации также изменяется. Поэтому необходимо знание и скорости изменения концентрации во времени, т. е. производной dCldt, что дается вторым законом Фика:

dC d2C

(IX, 15)

dt ~ ° d x 2

Основная трудность в применении обоих законов Фика до недавне­ го времени заключалась в определении коэффициента диффузии D. Однако трудности определения этого коэффициента для растворов и золей были преодолены после того, как Эйнштейн, изучая броуновское движение, обнаружил связь этого коэффициента со средним сдвигом Ах [уравнение (IX,11)1. Используя закон Стокса, Эйнштейн нашел за­ висимость коэффициента диффузии от вязкости среды и радиуса частиц [уравнение (IX, 12)]. Диффузионный метод определения размера частиц в настоящее время дает для коллоидных растворов наиболее надежные результаты.

Изучение броуновского движения и диффузии в коллоидных сис­ темах помогло глубже вскрыть природу дисперсных систем, а также установить общность молекулярно-кинетических свойств этих систем

исистем молекулярной дисперсности. Оно подтвердило реальное суще­ ствование молекул и явилось убедительным обоснованием правильно­ сти материалистического мировоззрения. Дальнейшее более детальное

иуглубленное изучение броуновского движения привело к созданию так называемой теории флуктуаций.

Флуктуация представляет собой самопроизвольное отклонение плот­ ности, концентрации или параметра от среднего равновесного значе­ ния в микрообъемах системы. Так, Сведберг, наблюдая явление флуктуации при подсчете числа частиц, находящихся в 1000 мк3золото­ го золя, нашел, что в среднем число частиц составило 1,545, но в от­ дельные моменты оно изменялось в пределах от 0 до 7. Отклонения мож­ но объяснить тем, что хаотическое движение частиц приводит к случай­ ному попаданию в выделенный микрообъем то большего, то мень­ шего числа частиц.

Таким образом, флуктуация представляет собой явление как бы обратное, явлению диффузии, хотя оба они — результат теплового движения. Если диффузия как всякий самопроизвольный процесс дол­ жна, в соответствии со вторым началом термодинамики, идти необра­ тимо, то флуктуация указывает на то, что второе начало термодинамики имеет статический характер, т. е. оно не применимо к отдельным ин­ дивидуальным частицам или к малому числу их. В обоих явлениях мы видим одно из доказательств справедливости закона материалистиче­ ской диалектики — единства противоположностей.

-386 —

Осмотическое давление. Для коллоидных растворов, как и для ис­ тинных, характерно осмотическое давление. Оно подобно газовому дав­ лению, является коллигативным свойством растворов, т. е. зависящим только от числа свободно движущихся коллоидных частиц.

Если учесть, что коллоидные частицы по сравнению с молекулами низкомолекулярных веществ обладают значительно большими размера­ ми и массой, то при одной и той же весовой концентрации коллоидного и истинного растворов в единице объема золя частиц содержится зна­ чительно меньше, чем в единице объема истинного раствора. Вот по­ чему по сравнению с последними коллоидные растворы обладают ни­ чтожно малым осмотическим давлением.

Так, 1%-ный золь золота имеет осмотическое давление, равное 0,00045 атм, а раствор сахарозы той же концентрации и в тех же ус­ ловиях 0,725 атм. Кроме того, какая-то доля измеряемого осмотиче­ ского давления в коллоидных растворах (главным образом гидрофоб­ ных) обусловливается примесью электролитов.

Поскольку коллоидные растворы принципиально не отличаются от истинных растворов, к ним можно применить формулу Вант-Гоффа:

где П — осмотическое давление золя, п — количество коллоидных частиц (в кмоль) в V л золя. Под киломолем коллоидных частиц подра­

Na

откуда

R T

(IX, 17)

No'

Относительно малые концентрации коллоидных растворов обуслов­ ливают также ничтожно малые значения всех других величин, завися­ щих от числа частиц в растворе (частичной концентрации). Так, все коллоидные растворы обладают чрезвычайно малым понижением упру­ гости пара, ничтожными (практически не поддающимися эксперимен­ тальному измерению) величинами понижения температур замерза­ ния и повышения температур кипения. Так, понижение температуры замерзания золя золота концентрации 1 г1л при размере частиц 4 ммк равно всего 0,000004°.

Между осмотическим давлением /7, числом частиц в единице объе­ ма п и средним радиусом г можно установить определенную зависи­ мость. Как известно, весовое количество диспергированного вещества в единице объема равно 4/3лгЫп, где d — плотность раствора. Исходя из этого для двух дисперсных систем с одинаковой дисперсионной сре­

дой при одинаковой температуре можно записать:

Для отсчета берут разность давлений в манометре, при которой уро­ вень толуола в капилляре остается постоянным в течение длительного промежутка времени. В этом случае осмотическое давление золя ком­ пенсируется внешним давлением. Все измерения осмотического давле­ ния необходимо производить при строго постоянной температуре. При измерении давления в манометре в сантиметрах водяного столба и при 25° С осмотическое давление вычисляется по формуле:

где С — концентрация золя или высокомолекулярного соединения, выраженная в г на 100 мл, М — молекулярный вес.

Так, если 1 г белка растворен в 100 мл воды (С = 1) при 25° С, молекулярный вес белка М. == 10 000, то осмотическое давление П рас-

— 388 —

твора будет равно:

/7 = 2,53-10’ -1,0 = 25,3 см Н.О.

10000

Мембранное равновесие Доннана. Более детальное изучение осмо­ тического давления коллоидных растворов показало, что даже приме­ нение в качестве внешней жидкости ультрафильтрата этого же золя не дает результатов, которые бы точно соответствовали теоретическим. В некоторых случаях экспериментально определенное осмотическое давление того или иного золя было больше теоретического, оно не за­ висело в ряде случаев от концентрации коллоида или изменялось не пропорционально концентрации его и т. п. Как показали более уг­ лубленные исследования, проведенные в свое время Доннаном, причи­ на подобных отклонений кроется в особом равновесии электролитов, которое устанавливается в присутствии частиц (или ионов), не способ­ ных проникать через полупроницаемую мембрану.

Впоследствии само явление неравномерного распределения какогонибудь электролита по обе стороны полупроницаемой мембраны под влиянием коллоидного электролита получило название мембранного равновесия Доннана.

Рассмотрим основные положения теории мембранного равнове­ сия.

Пусть имеется сосуд, разделенный на две части полупроницаемой мембраной, которая способна свободно пропускать ионы электроли­ тов, но задерживает коллоидные частицы. В одной стороне этого сосуда помещен раствор, содержащий электролит Na+ и коллоидный анион R- , задерживаемый мембраной.

По другую сторону мембраны в этом же сосуде находится электро­ лит NaCl, оба иона которого могут свободно проходить через мембра­ ну. Состав растворов в сосуде в начале процесса можно представить следующей схемой:

В этой схеме буквами Сх и С2 обозначены начальные концентрации со­ ответствующих ионов.

По истечении некоторого промежутка времени ионы Na+ и С1“ на­ чнут свободно проходить из правой половины сосуда в левую. Причем коллоидный анион R- все время остается в левой половине сосуда. Перемещение ионов закончится установлением динамического равно­ весия, т. е. количество ионов, переходящих в единицу времени в ту и Другую стороны, будет одинаково. Обозначая через х количество ио­ нов Na+ и С1~, перешедших из правой половины сосуда в левую, сос­ тояние равновесия по обе стороны мембраны можно представить сле­ дующим образом:

— 389