
книги из ГПНТБ / Бокштейн, С. З. Диффузия и структура металлов
.pdfТ е м п е р а т у р н ая зависимость |
времени |
релаксации |
||||||
при |
возврате |
и возбуждении |
описывалась |
уравнением |
||||
Аррениуса. |
Полученные |
значения энергии |
активации |
|||||
диффузии |
л о дислокациям |
менялись |
в довольно широ |
|||||
ких |
пределах: |
примерно |
от 41,8 до |
146,4 |
кдок/г-атом |
|||
(примерно |
от |
10 000 д о 35 000 |
кал/г-атом). |
Н а п р и м е р , |
||||
для |
сплавов |
С и + 0 , 0 1 % В |
и C u + 0 , 0 1 % La—53, 2 и |
|||||
149 |
кдж/г-атом |
(12700 и |
35600 кал/г-атом). |
Значение |
||||
энергии |
дислокационной |
д и ф ф у з и и — 1 2 5 , 5 |
|
кдж/г-атом |
||||||||||||||||
(30 000 кал/г-атом) |
|
дл я сплава |
N i + 0,005% |
Zr находится |
||||||||||||||||
между значением |
энергии |
|
активации |
|
зернограничной |
|||||||||||||||
самодиффузии, |
|
полученным |
в |
работе |
|
[107] —162 |
||||||||||||||
кдж/г-атом. |
(38500 |
кал/г-атом) |
и полученным |
в |
работе |
|||||||||||||||
[80] — 104 кдж/г-атом |
(24800 |
кал/г-атом). |
|
|
|
|
|
|
||||||||||||
Энергия активации диффузии но дислокациям в за |
||||||||||||||||||||
висимости от |
атомного |
радиуса |
диффундирующего |
в |
||||||||||||||||
медь элемента меняется |
по линейному |
|
закону |
(рис . 15) . |
||||||||||||||||
По |
мнению |
авторов, |
это ^ |
|
|
|
|
|
|
|
|
|
|
|
||||||
свидетельствует |
|
о |
том, | |
|
I |
- |
|
|
|
|
|
|
|
|
||||||
что |
механизм |
диффузии |
£ |
|
' |
|
|
|
|
|
|
|
|
|
||||||
исследованных |
примесей 1" |
^Е(ЗО) |
|
|
г,- |
Ge |
^ |
|
|
|
||||||||||
вдоль дислокаций |
в меди |
| [ |
|
|
|
|
J i |
в |
|
|
|
|
|
|||||||
одинаковый |
и |
носит |
ва- § 8Ь(20І\ |
|
|
|
|
|
|
|
|
|
||||||||
кансионный |
характер |
|
в |
I |
|
|
|
|
|
|
|
|
|
|
|
|||||
отличие |
от |
представле- -к М(Ю)if |
|
|
|
|
|
1 |
|
|
||||||||||
ний, |
развитых |
в |
работе |
^ |
|
|
1 |
1 |
|
1 |
1 |
|
1 |
|
||||||
|
|
о,1(1) оШШШШШШцгр) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Г 7 1 } - |
|
|
|
|
|
|
|
^ |
|
|
|
|
|
Г,НМ(А) |
|
|
|
|
||
Д л я |
расчета |
|
коэффи |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
циентов |
диффузии |
вдоль |
Р |
и с |
1 5 3 а в и с и м о с |
т ь |
э н |
е р г и и |
а к . |
|
||||||||||
дислокаций из амплитуд- |
тнвации диффузии |
по |
дислокаци- |
|||||||||||||||||
НОЙ зависимости |
внутрен- |
ям Q от атомного |
радиуса диф- |
|||||||||||||||||
него трения была опреде- |
|
Фундирующего |
в |
медь |
элемента |
|||||||||||||||
лена |
величина |
дислока |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ционного |
сегмента — L |
c . |
В |
сплаве Cu + 0,01% |
L i темпе |
|||||||||||||||
ратурная |
зависимость |
|
коэффициента |
|
диффузии |
вдоль |
||||||||||||||
дислокаций £ >д=0,04 ехр (—20000/ЯГ). |
|
|
|
|
|
|
|
|
||||||||||||
При |
исследовании |
диффузии |
вдоль |
|
дислокаций |
в |
||||||||||||||
меди, ж е л е з е и алюминии методом внутреннего |
трения |
|||||||||||||||||||
было замечено, |
что возврат |
|
внутреннего |
|
трения |
для |
||||||||||||||
трех |
различных |
металлов |
наблюдается |
|
нри |
близких |
||||||||||||||
гомологических |
температурах |
(0,3—0,35 Tsa). |
Д л я же |
|||||||||||||||||
леза |
при изменении |
температуры |
от 230 до |
320° С |
вре |
|||||||||||||||
мя |
возврата |
уменьшалось |
с |
S ч д о 30 мин; |
у |
меди |
||||||||||||||
51
т а к ое время отмечалось при |
130 |
и 240°С |
соответствен |
|
но, а у алюминия временная |
зависимость |
наблюдалась |
||
при комнатной температуре . |
|
|
|
|
Методом |
внутреннего трения |
исследовали т а к ж е |
||
диффузию |
германия вдоль |
расщепленных |
дислокаций, |
|
расположенных в плоскостях { і п | » в разбавленных медных растворах [64] . Авторы рассматривали компо
ненту временной |
зависимости |
|
затухания |
внутреннего |
|||||||||
трения, которая связывалась с перераспределением |
ато |
||||||||||||
мов растворенного вещества |
вдоль |
ядер |
дислокаций . |
||||||||||
Затухание |
во |
времени |
после |
снятия |
н а п р я ж е н и я |
|
воз |
||||||
буждения |
происходило в |
соответствии с |
расчетом |
по |
|||||||||
экспоненте. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно |
полученным |
данным |
D ° = 0 , 0 1 |
|
см2/сек, |
|||||||
(2д=1,26 эв, QH /Qo6—0,7. |
По |
мнению авторов |
работы |
||||||||||
[54], отклонение |
величины |
DR |
от |
истинной |
величины |
||||||||
возможно, |
по крайней |
мере, « а |
порядок из-за |
неточнос |
|||||||||
ти |
в определении |
L c p |
(среднее |
|
расстояние |
между |
точка |
||||||
ми |
закрепления |
в положении |
равновесия) ; в расчетное |
||||||||||
уравнение |
(17) оно входит во 2-й степени. |
|
|
|
|
||||||||
|
Р о ж а н с к и й измерял самодиффузию вдоль |
дислока |
|||||||||||
ций в цинковой фольге, используя электронную |
микро |
||||||||||||
скопию на |
просвет. Коэффициент диффузии |
вакансий |
|||||||||||
определяли по скорости округления дислокационных пе тель. Рассчитанный из этих данных коэффициент само диффузии цинка вдоль дислокаций оказался на 10 по
рядков больше, |
чем коэффициент |
объемной |
самодиф |
|||
фузии |
( ~ 1 0 - 9 |
и 10~1 9 см2/сек); |
последний |
получен |
||
экстраполяцией. |
|
|
|
|
||
В последнее время непосредственное измерение диф |
||||||
фузии |
вдоль |
дислокаций было изящно |
сделано Воли |
|||
ным |
[116]. |
Самодиффузию измеряли на |
алюминиевой |
|||
фольге, которую можно было исследовать методом про свечивающей электронной микроскопии. Фольга имела
изолированные |
сферические |
поры [радиус |
10—20 нм |
||
о |
|
|
|
|
|
(100—200 А) ] |
и поры, соединенные с |
поверхностью |
|||
единичными дислокациями . |
Это |
были |
расщепленные |
||
дислокации с вектором Бюргерса Ь=-—<_[ |
10і> . В про |
||||
цессе отжига и те и другие поры |
с о к р а щ а л и с ь |
в резуль |
|||
тате диффузионного подвода атомов от поверхности к порам под влиянием капиллярных сил, Однак о поры,
52
соединенные дислокацияіми с поверхностью, |
сокращались |
|
быстрее. Учитывая разницу в скорости сокращения |
изо |
|
лированных « неизолированных пор, можно |
было |
оце |
нить перенос вещества вдоль дислокаций. |
|
|
Предполагая вакансионный механизм диффузии |
как |
|
в решетке, так и по дислокациям, авторы |
определили |
|
параметр £>д , характеризующий перенос массы в резуль тате самодиффузии вдоль дислокаций:
где од — коэффициент |
диффузии вдоль |
дислокаций; |
||||||
Л д — площадь ядра |
дислокаций; |
|
|
|
||||
|д—- температурно |
зависимый фактор |
корреляции |
||||||
|
для самодиффузии по дислокациям с помощью |
|||||||
|
вакансионного механизма . |
|
|
|
||||
Д и ф ф у з и я |
подчинялась |
зависимости |
Аррениуса |
|||||
£д=А> |
exçi—QxIRT). |
|
|
|
|
|
||
Энергия активации самодиффузии алюминия состав |
||||||||
ляла 1,36-Ю-1 9 дою (0,85 эв), |
a Q„/Q O 6~0,6 . |
|
|
|||||
Б ы л а |
изучена [101] |
самодиффузия в |
монокристалле |
|||||
серебра |
A g u 0 |
по дислокационным трубкам |
в |
интервале |
||||
258—448° С методом |
снятия |
химическим |
путем |
тончай- |
||||
|
|
10 нм |
|
о |
|
|
|
|
ших слоев ~ |
(100А). |
Определенная |
из |
низкотем |
||||
пературной части графика Аррениуса энергия активации
диффузии, равная 75,4 |
кдою/г-атом |
(18000 |
кал/г-атом), |
|||||||
согласуется |
с |
результатами, |
полученными |
в |
работе |
|||||
[66] — 82,5 кдоіс/г-атом |
(19700 |
кал/г-атом) при |
исследо |
|||||||
вании диффузии вдоль |
мало - и |
среднеугловых |
границ |
|||||||
наклона |
(см . гл . I I I ) . В |
согласии |
с |
результатами |
этой |
|||||
работы |
находилось т а к ж е значение |
коэффициента |
диф |
|||||||
фузии вдоль |
дислокаций D = |
1,2-10— 1 2 см2/сек |
|
(258°С) . |
||||||
Вуттиг и Бирнбаум |
[62] изучали |
самодиффузию |
ни |
|||||||
келя в тонких |
монокристальных |
образцах, |
с о д е р ж а щ и х |
|||||||
краевые |
дислокации в направлении |
[211] |
перпендику |
|||||||
лярно к поверхности. Плотность дислокаций |
составляла |
|||||||||
~ Ю - 7 см~2, |
расстояние |
между |
ними |
было ~ |
3 мкм; |
сле |
||||
довательно, они располагались достаточно просторно. В процессе изотермического отжига в зависимости от вре мени измеряли активность диффундирующего никеля на грани, противоположной той, на которую наносился
53
|
О т ж и г проводили |
при температурах, |
когда |
диффу |
||
зия |
в решетке была |
ничтожно |
м а л а . Условия опыта |
поз |
||
волили раздельно определить |
Л д (коэффициент |
диффу |
||||
зии |
вдоль дислокации) и А д |
(сечение |
дислокационной |
|||
трубки), поскольку результаты измерений зависели |
от |
|||||
величины отсоса из дислокационной трубки в объем, ко
торый в свою очередь |
зависел |
от радиуса |
трубки. |
|
|||||
Авторы получили |
Л д г « 3 - 1 0 ~ 1 3 см2, |
что |
примерно |
па |
|||||
два порядка больше |
обычных |
оценок |
площади |
сечения |
|||||
дислокационной трубки. Величины DR |
и QR |
составляли |
|||||||
соответственно 20 см2/сек |
и 1,6 |
эв, |
a |
Q n /Q O 6 ~0,5 . |
|
|
|||
Этим ж е методом |
исследовали |
диффузию |
N i 6 |
3 в мо |
|||||
нокристальных образцах сплава N i + 6 0 % С о . |
Дислока |
||||||||
ции были диссоциированы |
вдоль |
[211]. |
П р е д с т а в л я л о |
||||||
интерес оценить роль |
энергии |
дефектов |
упаковки, |
по |
|||||
скольку в таком сплаве она примерно в 5 раз меньше,
чем в чистом никеле. |
|
О б р а з ц ы |
изгибали вокруг |
оси |
|||||||||||
[121], |
при этом |
в плоскости |
скольжения |
(111) |
генери |
||||||||||
ровались |
дислокации |
в |
количестве |
— 0,5 -107 |
см-2. Об |
||||||||||
разцы |
вырезали параллельно |
[121] |
и после |
полировки |
|||||||||||
подвергали |
отжигу при 900°С |
в вакууме |
1,33-'10~5 |
нім2 |
|||||||||||
( Ю - 7 |
тор). |
Н а |
полированную |
поверхность |
наносили |
||||||||||
|
|
3 толщиной ~ 100 нм |
|
|
|
о |
|
|
|
|
|||||
слой N i 6 |
(1000 А) |
и |
проводили |
||||||||||||
диффузионный |
отжиг |
в |
интервале |
506—618° С. В |
этой |
||||||||||
работе т а к ж е отмечена |
большая |
величина |
А д ~ Ю - 1 |
1 см2, |
|||||||||||
что на два порядка больше, чем |
величина |
А д , |
получен |
||||||||||||
ная в работе [62] . |
|
|
|
|
|
|
|
|
|
|
|
||||
Диффузия |
вдоль |
дислокационных |
|
рядов |
|
|
|
|
|||||||
Торнбалл и Гофман [56] исследовали |
самодиффузию |
||||||||||||||
серебра |
A g n 0 вдоль малоугловых |
границ |
с осью |
накло |
|||||||||||
на [001] и плоскостью границы |
(010). |
Т а к а я |
граница |
||||||||||||
согласно |
электронно-микроскопическим |
|
исследованиям |
||||||||||||
может |
быть |
представлена |
рядом |
равномерно |
располо |
||||||||||
женных дислокаций в д о л ь [001] |
с |
вектором |
Бюргерса |
||||||||||||
Ь = а |
[010] либо равномерно и близко |
расположенными |
|||||||||||||
парами дислокаций |
вдоль |
того ж е |
направления |
с Ь = |
|||||||||||
= а/2 |
['ПО] л Ь — а/2 |
[ П О ] , где а — параметр |
решетки |
||||||||||||
(рис. |
16). Величину эффективного потока |
вдоль |
к а ж д о й |
||||||||||||
дислокации |
или пары |
дислокаций |
|
определяли |
из |
|
соот |
||||||||
ношения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Ргр — эффективный |
поток вдоль |
границы; |
|
|
0 — у г о л наклона |
границы. |
|
|
|
Д и ф ф у з и я осуществлялась |
из тонкого слоя |
серебра, |
||
электролитически осажденного |
на |
поверхность |
(001). |
|
Величину Рв из (13) рассчитывали |
с помощью уравнения |
|||
Фишера [57] . |
|
|
|
|
Рис. 16. Возможная дислокационная структура малоугловых на клонных границ
Показано, что диффузия вдоль единичных или пар ных дислокаций идет с одинаковой скоростью дл я гра ниц с углом наклона 9,13 и 16°, т. е. не зависит от Ѳ (или расстояния между дислокациями / д ) . Расстояние между одиночными или парными дислокациями составляет
2,6 нм |
(26 А) — 9 ° , 1,8 нм |
(18 А) — 13° и |
1,5 |
нм |
(15 А) — |
|
|||
16°. В этом случае ядра дислокаций хорошо |
разделены . |
||||||||
Согласно |
полученным |
результатам |
|
параметры |
са |
||||
модиффузии |
серебра вдоль дислокаций |
Я» |
= . 5 , 2 - Ю - 1 |
7 |
|||||
см4/сек, |
Q ; ( = 1,18-10~19 док |
(0,74 эв); |
дл я |
решетки |
— |
|
|||
£ » 0 = 0 , 4 4 см2/сек, a Q = 3,07-10~1 9 док |
(1,92 |
эв); |
следо |
|
|||||
вательно, QJQÏZ 0,4.
Анализ Фишера (и более тонкий Уиппла) предпола гает на поверхности постоянство концентрации, что тре бует большой скорости поверхностной диффузии . По -
55
скольку нет прямого подтверждения |
|
соблюдения |
этих |
||||||
граничных условий, полученными результатами |
следует |
||||||||
пользоваться с осторожностью. |
|
|
|
|
|
|
|
|
|
Ш ь к ж о н [58] т а к ж е исследовал |
самодиффузию |
се |
|||||||
ребра, однако не вдоль наклонных границ, как |
в [ 5 6 ] , а |
||||||||
вдоль границ кручения. Сравнивая полученные |
резуль |
||||||||
таты авторы пришли к выводу, |
что коэффициент диффу |
||||||||
зии вдоль винтовых дислокаций в серебре |
на |
порядок |
|||||||
меньше, чем вдоль краевых. Однако |
электронномикро- |
||||||||
скопические исследования на просвет |
[59] |
показывают, |
|||||||
что границы кручения при относительно больших |
углах |
||||||||
(Ѳ~24°) |
нельзя описать с помощью |
простого |
ряда |
дис |
|||||
кретных |
дислокаций. Поэтому |
полученные |
|
результаты |
|||||
[58] не могут быть непосредственным |
доказательством |
||||||||
более высокой диффузионной |
проницаемости |
|
винтовых |
||||||
дислокаций [ 3 ] . |
|
|
|
|
|
|
|
|
|
Б ы л а |
исследована самодиффузпя |
|
никеля |
|
[60] |
как по |
|||
чисто наклонны-м границам, так и по границам |
кручения |
||||||||
(оси кручения < 1 1 1 > ) . Использовав |
анализ |
Уиппла |
и |
||||||
применив дл я расчетов электронно-вычислительную ма
шину, |
авторы |
нашли: |
Р в = 2 , 2 - 1 0 - 8 |
см^-секг1; |
|
Qu— |
||||||
— 2,82-10~1 9 дж (1,76 эв); |
QA /Q o c~0,6 |
(для |
наклонных |
|||||||||
границ); |
Р% =2,6-10~8 |
см^-сек^; |
Qn=3,\2-10~19 |
дж |
||||||||
(1,95 эв); |
Qfl/Qoa~0,7 (для границ |
кручения) . |
|
|
||||||||
Следует иметь в виду, что структура |
дислокационных |
|||||||||||
рядов |
в данном |
случае дл я |
малоугловых |
границ |
обоих |
|||||||
типов |
осложняется обычно |
расщеплением |
дислокаций в |
|||||||||
плоскости (111) на частичные, связанные дефектом |
упа |
|||||||||||
ковки, |
и |
быстрая диффузия, |
по-видимому, |
происходит |
||||||||
главным образом в ядре частичных дислокаций. В |
этом |
|||||||||||
случае различие в коэффициентах диффузии вдоль |
дис |
|||||||||||
локации дл я малоугловых границ |
наклона |
и |
кручения |
|||||||||
будет |
меньше, чем это следует из данных работ |
.Кэнона |
||||||||||
и С т а р к а . Этот |
вопрос |
проанализирован |
Б а л л у ф ф и [54] . |
|||||||||
іКроме того, |
изучали |
самодиффузию |
N i 6 3 |
вдоль |
крае |
|||||||
вых дислокаций в малоугловых границах в никеле [61] . Анализ данных этой работы показывает, что в пределах 5—10° энергия активации диффузии не зависит от углов
разориентировки. Д л я 0 = 4 0 ° |
авторы |
получили |
следую |
щую зависимость: |
|
|
|
РГ р = 4,6-10~" ехр (— 1,08 эв/kT) |
см*-сек~х |
; |
|
Qn/Qob ~ |
0,4. |
|
|
56
Следует отметить, что образование в металле полигоиизованной структуры может привести к уменьшению
общего диффузионного потока, вероятно, вследствие |
то |
|||||||||
го, что при этом происходит |
частичное |
очищение |
|
тела |
||||||
зерна от дислокаций и концентрация их |
на |
малоугловых |
||||||||
границах. |
|
|
|
|
|
|
|
|
|
|
•В работе |
[108] было |
проведено |
сравнительное |
иссле |
||||||
дование самодиффузии никеля в никелевом |
сплаве |
|||||||||
(ХН77ТЮ) после обычной обработки и |
после обработ |
|||||||||
ки, в результате которой возникает |
полигональная |
|||||||||
структура. П е р в а я состоит |
из з а к а л к и |
с |
іГ080°С, |
8 ч, |
||||||
охлаждения |
на |
воздухе |
и старения |
при |
700°С, 16 |
ч; |
вто |
|||
р а я — т а к ж е |
из |
з а к а л к и |
на |
воздухе |
с 1080°С, |
8 ч, |
затем |
|||
деформации растяжением на 0,3%, полигонизации |
при |
|||||||||
550°С, 200 ч |
и старения |
при |
700°С, 16 ч. В данном |
случае |
||||||
надо иметь в виду, что старение приводило |
к |
выделению |
||||||||
из ^-твердого раствора дисперсной v' - фазы на |
дислокаци |
|||||||||
онных стенках |
и закреплению их. Коэффициенты диффу |
|||||||||
зии определяли абсорбционным методом с использовани
ем N i 6 3 . Поверхностный наклепанный слой снимали |
|||
электролитической |
полировкой. |
Скорость |
диффузии в |
поверхностном слое |
образцов, |
подвергнутых |
механико- |
термической обработке (МТО) для получения полигони-
зованной |
структуры, была при |
800°С в два раза меньше, |
|
чем в образцах после |
обычной |
термической обработки |
|
(2,4-'Ю-1 2 |
и 4 , 5 - Ю - 1 2 |
см2-сек-1). |
|
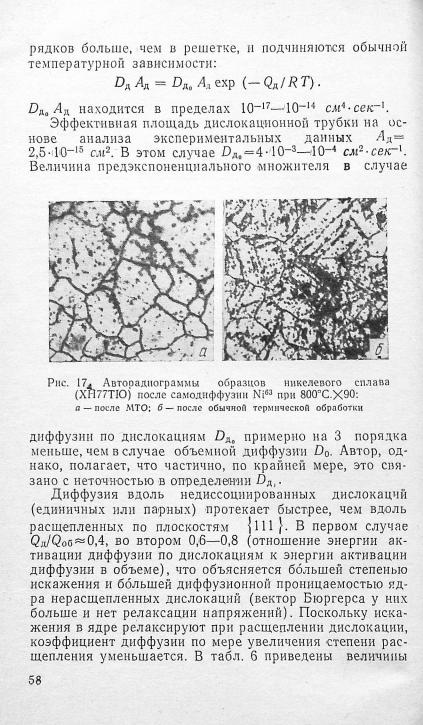
На рис. 17 показаны авторадиограммы после обеих обработок. После М Т О по сравнению с обычной терми ческой обработкой путей преимущественной диффузии меньше: диффузия происходит в основном по границам зерен и немного внутри зерна; после обычной обработки наблюдается значительная диффузия внутри зерна по «бывшим» линиям скольжения и дефектным участкам структуры.
Характерно, что наряду с замедлением |
диффузии |
||
после М Т О наблюдается |
повышение |
длительной прочно |
|
сти; при 800°С время до |
разрушения |
возрастает |
в 2 раза . |
Детальный анализ результатов экспериментальных измерений диффузии вдоль дислокаций, проведенных различными методами, главным образом в г.ц.к. метал лах (Ag, Ni, A l и др . ), сделан Б а л л у ф ф и в работе [64] . Автор приходит к следующим основным выводам: коэф фициенты самодиффузии по дислокациям на много по-
57
расщепления со частичных дислокаций с вектором Бюр - герса b = -~ < 1 1 0 > в различных металлах .
|
|
|
|
|
Т а б л и ц а |
6 |
|
Величины |
расщепления со частичных дислокаций в AI, Ni и Си |
||||||
Металл |
Энергия дефекта упаковки -у, |
С, !0««/л |
Ь, нм ( А ) |
w, нм{ А) |
|||
|
мдяс/н' |
(зрг/смг) |
|
||||
AI |
|
135 |
(135) |
2,65 |
0,286(2,86) |
0,75(7 |
,5) |
Ni |
|
240 |
(240) |
9,47 |
0,250(2,50) |
1,14(11,4) |
|
Си |
|
80 |
( 80) |
5,46 |
0,256(2,56) |
2,04(20,4) |
|
Величину «в определяли из |
соотношения |
|
|
|
|
||||||
|
|
|
о) = |
G а 2 |
|
• |
2 + V |
|
|
|
|
|
|
|
|
|
' — , |
|
|
|
|
||
|
|
|
|
48 л у |
|
1 — ѵ |
|
|
|
|
|
где |
G — модуль |
сдвига; |
|
|
|
|
|
|
|
||
|
V—•коэффициент Пуассона. |
|
|
|
|
||||||
|
Из таблицы |
видно, |
что |
наиболее |
диссоциированы |
||||||
дислокации в |
меди, а в них, как отмечалось, наиболее |
||||||||||
низкие коэффициенты диффузии . |
|
|
|
|
|||||||
•Согласно [54] в случае |
вакан-сионного |
механизма |
|||||||||
|
|
|
QA = |
Qo6p+ $ |
+ |
|
|
|
(21) |
||
где |
Qo6p — энергия образования |
вакансий |
в |
решетке; |
|||||||
|
QM—энергия миграции |
вакансий |
в |
|
я д р е |
дисло |
|||||
|
кации; |
|
|
|
|
|
|
|
|
||
|
QB—энергия связи вакансии с ядром |
дислокации . |
|||||||||
|
Оценка (2Я |
в р а м к а х |
этой |
модели соответствует |
экспе |
||||||
риментальным |
данным . |
|
|
|
|
|
|
|
|
||
|
Д и ф ф у з и я |
в дислокациях |
с |
большой |
скоростью про |
||||||
текает в ядре вдоль узкой полосы шириной в несколько
векторов |
Бюргерса и с |
меньшей скоростью вдоль полосы |
||
дефекта |
упаковки, с в я з ы в а ю щ е г о |
частичные |
дислокации . |
|
'Скорость диффузии |
зависит |
от вида |
дислокации. |
|
Вдоль диссоциированных краевых дислокаций с одина ковым вектором Бюргерса она больше, чем вдоль диссо циированных винтовых дислокаций. В никеле дл я мало угловых наклонных границ с углом раз-ориентировки 10° скорость примерно в 5 раз больше, чем в границах кру чения. Это различие тем больше, чем меньше винтовые
59
дислокации склонны к расщеплению, так к а к при расщеп лении появляется- краевая компонента.
Анализ показывает, что в диффузионных измерениях, выполненных на малоугловых границах, эффект пере крытия полей напряжения мал. Он не может 'быть суще
ствен, если «быстрая» диффузия идет |
вдоль узкой труб |
||
ки сечением Л д = 2 , 5 . 1 0 ~ 1 5 см'2. |
В этих условиях |
диффузия |
|
вдоль дислокаций в плоских скоплениях по |
малоугло |
||
вым границам и в изолированном |
состоянии |
д о л ж н а |
|
быть одинаковой. Это не относится к случаю |
расщепле |
||
ния дислокаций. Н а п р я ж е н и я |
могут |
изменить |
степень |
расщепления дислокации и, как это вытекает из преды
дущего, изменить скорость |
диффузии — сокращение |
рас |
|
стояния между частичными |
дислокациями уменьшает |
||
релаксацию, увеличивает локальные искажения |
в |
ядре |
|
и, следовательно, ускоряет |
диффузию . В случае |
модели |
|
парных дислокаций эффекты перекрытия между смеж ными дислокациями в каждой паре могут оказывать со ответствующее влияние на диффузию в зависимости от расстояния между дислокациями . В общем случае, если принять вакансионную модель, то перекрытие полей на пряжений должно приводить к замедлению диффузии изза влияния гидростатического давления Р на концентра цию и сіщзость миграции вакансий. Это вытекает из сле дующего соотношения:
г, |
/ \ |
|
р, |
/ \ |
ехр |
/ |
<2д + (^обр + |
Ю Р |
\ |
/ о т |
|
Яд |
(Р) |
= A u |
(р) |
^ |
|
^ |
|
j , |
(22) |
||
где Ѵобр — активационный |
объем |
образования |
вакансий |
||||||||
|
в |
ядре; |
|
|
|
|
|
|
|
|
|
Ѵ м — активационный объем |
миграции; |
|
|
|
|||||||
р — гидростатическое |
давление, р а в н о е — 7 з ( с г ы + |
||||||||||
|
+ |
0 2 2 + |
0 3 3 ) |
( О І І — нормальное |
н а п р я ж е н и е ) |
||||||
Однако эффект мал, так как р(Ѵ0бр+Ѵм) |
мало |
по от |
|||||||||
ношению к <2д, если допустить, |
что ( Кобр + |
Ум) |
порядка |
||||||||
одного атомного |
объема. |
|
|
|
|
|
|
||||
Анализируя |
имеющиеся |
экспериментальные |
данные, |
||||||||
автор пришел к выводу, что они не противоречат |
вакан - |
||||||||||
сионному |
механизму диффузии |
по дислокациям, а |
в п о : |
||||||||
следнем эффект корреляции слабо зависит от темпера туры и составляет всего несколько десятых. Однако на помним, что результаты исследований [70—73] больше
60
