58

Волновая оптика

Лабораторная работа 3-ВО (б)

ДИФРАКЦИЯ ФРЕНЕЛЯ НА КРУГЛОМ ОТВЕРСТИИ

Цель работы: Изучение явления дифракции света на примере дифракции Френеля.

Приборы: Лабораторный оптический комплекс ЛКО-3: оптическая скамья, гелий – неоновый лазер, винтовой окулярный микрометр, набор универсальных принадлежностей.

Методические указания по организации самостоятельной работы

1. Изучите теоретический материал по конспекту лекций и учебникам: [4: §177-180]; [3: §125-129], [1].

2. Изучите описание лабораторной работы.

3. Подготовьте конспект и бланк отчета по лабораторной работе [2].

4. Подготовьте ответы на контрольные вопросы к допуску и защите лабораторной работы:

1. Электромагнитная теория света. Уравнение, свойства световых волн.

2. Энергия световой волны. Вектор Пойнтинга. Интенсивность света.

3. Явление дифракции света. Параметр дифракции m. Виды и области наблюдения дифракции.

4. Дифракция Френеля. Принцип Гюйгенса-Френеля. Метод зон Френеля.

5. Оптическая схема наблюдения дифракции Френеля и Фраунгофера.

6. Вывод расчетных формул.

Теория метода и описание установки

Дифракция Френеля наблюдается в ближней зоне дифракции (L ~ L_{д ,} m =1) и является наиболее сложным видом дифракции. Для расчета амплитуды и интенсивности световых колебаний (волнового поля) дифракционной картины Френеля используют метод зон Френеля, основанный на принципе Гюйгенса-Френеля.

Рассмотрим плоскую монохроматическую волну длиной , падающую нормально на экран Э₁, параллельно его оси симметрии ОР (рис. 3.3). Экран Э₁ определяет положение волновой поверхности в рассматриваемый момент времени.

Согласно принципу Гюйгенса-Френеля волновое поле на экране Э₂ рассчитывается как результат суперпозиции элементарных волн, испускаемых «вторичными» когерентными источниками, расположенными на волновой поверхности в плоскости экрана Э₁.

Рис. 3.3.

Расчет показывает, что световое колебание, распространяющееся из точки В в точку Р, отстает по фазе от колебания, распространяющегося из точки О, на величину , равную

(3.14)

где L - расстояние между экранами Э₁ и Э₂, ρ- радиус отверстия.

Область волновой поверхности на экране Э₁, в пределах которой фаза приходящих в точку Р колебаний изменяется на , называется зоной Френеля. Первая зона Френеля является кругом радиуса ₁ с центром в точке О, в котором  изменяется в пределах: 0    . Вторая зона – кольцевая, в которой     . Последующие зоны Френеля также кольцевые и равенство   m определяет число m зон Френеля, укладывающихся внутри круговой области радиуса   _m. Следовательно,

, и

, (3.15)

, (3.16)

где _m – радиус внешней границы m-ой зоны Френеля.

Из сравнения формул (3.15) и (3.6) следует, что число m является параметром дифракции, определяющим вид дифракции.

Далее, рассмотрим падение на экран Э₁ расходящейся от точечного источника S волны (рис. 3.4а) или сходящейся в точке S волны (рис. 3.4б). Вычисление фазовых сдвигов  и числа m открытых зон Френеля в этом случае приводит к тем же формулам (3.14-3.15), что и для плоской волны, но L в них выражается в следующем виде:

Для расходящейся волны

= + , (3.17)

где l₁ – расстояние от фокуса волны до экрана Э₁,

l – расстояние между экранами Э₁ и Э₂.

Для сходящейся волны

= . (3.18)

Для плоской волны l₁  , L = l.

Рис. 3.4.

Если в сходящейся волне l = l₁, то L   и m  0, тогда в фокальной плоскости сходящейся волны наблюдается дифракция Фраунгофера. Эта возможность получения дифракционной картины Фраунгофера в фокальной плоскости сходящейся сферической волны используется при выполнении лабораторной работы.

Пусть экран Э₁ будет непрозрачным и в нем будет вырезано круглое отверстие радиуса . На экране Э₂ возникнет дифракционная картина Френеля от круглого отверстия, состоящая из концентрических светлых и тёмных колец, симметричных относительно оси отверстия (l  l₁). Интенсивность I света в центре картины для небольшого числа m открытых зон Френеля равна

I = I₀sin², (3.19)

где I₀ – интенсивность, когда экран Э₁ отсутствует.

Если в отверстии укладывается нечетное число m зон Френеля, то в центре картины наблюдается максимум интенсивности света I  4I₀. При четном числе m зон Френеля в центре возникает минимум интенсивности I. Это объясняется тем, что сдвиг фаз  колебаний соседних зон  = , и, следовательно, четные и нечетные зоны посылают в центр картины противофазные колебания. Угловой размер центрального светлого максимума I (или минимума) равен углу дифракции _д  .

При l = l₁ возникает дифракционная картина Фраунгофера, состоящая из центрального максимума интенсивности света I, окруженного темными и светлыми кольцами. Радиусы тёмных колец: R₁ = 0,61, R₂ = 1,12.

В лабораторной работе наблюдение дифракционных картин Френеля и Фраунгофера и измерения проводятся с помощью лабораторного оптического комплекса ЛКО-3, общий вид которого показан на рис. 3.5.

1.4 05 06 02 08 4 10 9 3 6

Рис. 3.5. 1.4 – экран со шкалой; 3 – оптическая скамья со шкалой; 4 – блок питания лазера; 6 – лазер-излучатель с линзой насадкой; 02 – модуль 02 (микропроектор); 05 – модуль 05 (конденсор); 06 – модуль 06 (объектив); 08 – модуль 08 (кассета для установки объектов); 9,10 – регулировочные винты.

Оптическая схема установки для наблюдения дифракции показана на рис. 3.6.

Рис. 3.6.

Порядок выполнения работы

1. Включите блок питания 4 в сетевую розетку и установите максимальную интенсивность излучения лазера регулятором блока питания (рис.3.5.) Лазер и ЛКО-3 включаются только в присутствии преподавателя или лаборанта.

2. Установите на оптическую скамью модуль 08 с объектом 47 (матовое стекло) в конце оптической скамьи у правой боковины установки и при помощи регулировочных винтов 9 и 10 совместите луч лазера с центром объекта 47.

3. Передвиньте модуль 08 вплотную к лазеру и регулировочными винтами 9 и 10 совместите луч лазера с центром объекта 47.

4. Повторите операции по п.п. 2,3 два-три раза, пока смещение светового пятна лазера от центра матового стекла не окажется меньше радиуса светового пятна лазера в обоих положениях модуля 08, и оставьте у правой боковины ЛКО-3.

5. Для создания сходящейся волны установите на оптическую скамью модуль 05 (конденсор – линза Л₁) вплотную к лазеру (координата .)

6. Регулировочными винтами модуля 05 совместите луч лазера с центром модуля 08.

7. Установите на оптическую скамью (координата ) модуль 06 (объектив О) и регулировочными винтами этого модуля совместите луч лазера с центром модуля 08.

8. Установите на оптическую скамью (координата ) модуль 02 (микропроектор – линза Л₂). Перемещая объектив (модуль 06), сфокусируйте световую волну в объектной плоскости Э₂ линзы Л₂ . На экране Э₃^’ при этом будет наблюдаться яркая точка минимальных размеров. Координата объектива .

9. Замените в модуле 8 объект 47 на объект 18 (отверстие с диаметром d=1мм – экран Э₁) и установите этот модуль на оптическую скамью возможно ближе к объективу, справа (координата ). В плоскости экрана Э₂ возникнет дифракционная картина Фраунгофера, которая отобразится на экране Э₃^’.Определите расстояние от экрана (модуль 08) с координатой до фокуса волны (экрана Э₂ с координатой ), 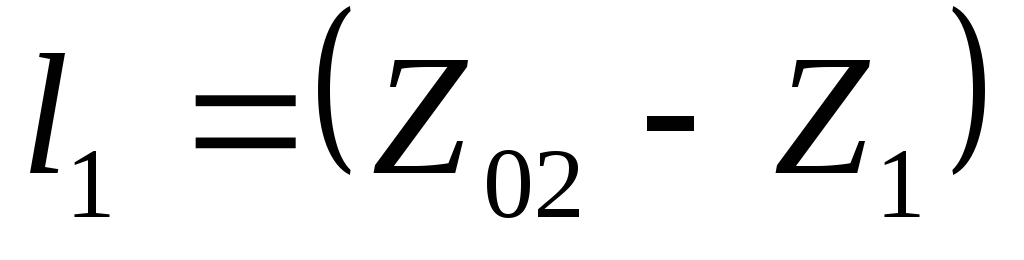мм. Данные запишите в таблицу, составленную по форме 3.2.

Форма 3.2.

Число зон m	0	2	3	4	5	6
	650
	0

10. Перемещая модуль 02 (экран Э₂) по направлению к модулю 8 (экрану Э₁), зафиксируйте изменение дифракционной картины Френеля при : чередование максимумов и минимумов интенсивности света в центре концентрических колец. Определите значения l (рис. 3.4 б), при которых открыты m=2,3,4,5,6 зон Френеля: , где - координата плоскости наблюдения (модуль 02), -координата экрана (модуль 08). Значения l запишите в таблицу, составленную по форме 3.2.

11. Вычислите по формуле (3.18) значение и . Результаты вычислений запишите в форму 3.2. Постройте график зависимости m от .Из формулы (3.15) вычислите длину волны λ.

12. Оцените абсолютную погрешность результата ΔL, учитывая приборную погрешность измерительных инструментов, которая равна

,

где коэффициент Стьюдента для надежности , γ - половина наименьшего деления линейки ().

Абсолютная погрешность ΔL равна:

.

Окончательный результат .

13. Результаты измерений.

Координата объекта : =____________мм.

Координата фокальной плоскости:

К началу

На следующую страницу

К оглавлению

К титулу