Физика-на май 2014-часть 2-бакалавр / Материалы комплекса / Лекции / Пособие по физике-2 часть-МИКХиС / Лекция 6_Магнитное поле

Курс лекций по физике. Часть II: Электромагнетизм 203

ЧАСТЬ II

Раздел 3. ЭЛЕКТРОМАГНЕТИЗМ

Лекция 6. Магнитное поле

и его характеристики

План лекции

6.1. Основные характеристики магнитного поля.

6.2. Закон Био–Савара–Лапласа и его применение к расчетам магнитных полей.

6.1. Основные характеристики

магнитного поля

Эксперимент показывает, что так же, как в пространстве вокруг электрических зарядов возникает электрическое поле, так и в пространстве, окружающем электрические токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие этого поля обнаруживается по силовому воздействию на внесенные в него проводники с током или постоянные магниты. Сам термин «магнитное поле» появился в 1820 г., когда датский физик Эрстед¹ обнаружил ориентирующее действие проводника с током на стрелку компаса. Было установлено, что в отличие от электрического поля (которое действует и на покоящиеся, и на движущиеся заряды), магнитное поле действует только на движущиеся электрические заряды. Подобно тому, как для исследования электрического поля используют малые электрические заряды, так и для изучения магнитного поля используют замкнутый плоский контур (рамку с током), размеры которого малы по сравнению с расстояниями до токов, образующих магнитное поле. Опыты показывают, что магнитное поле оказывает на рамку

с

Рис. 6.1

током ориентирующее действие, поворачивая ее определенным образом (обычно говорят: «…рамка с током свободно установилась в магнитном поле»). Для характеристики этого процесса вводят положительную нормаль , связанную с рамкой. Направление связанно с током в рамке по правилу правого винта (рис. 6.1). За

направление магнитного поля в данной точке принимается направление положительной нормали к рамке с током, свободно установившейся в магнитном поле.

Ориентирующее действие магнитного поля на рамку с током означает, что на рамку действует вращающий момент . Эксперимент дает зависимость

(6.1)

где – вектор магнитного момента рамки с током, характеризующий ее магнитные свойства; – вектор магнитной индукции, являющийся количественной характеристикой магнитного поля (направление определяет направление магнитного поля).

Для плоского контура с током

(6.2)

где S – площадь поверхности контура, – единичный вектор положительной нормали к поверхности рамки.

Направление , как следует из уравнения (6.2), совпадает с .

Если в данную точку магнитного поля помещать разные рамки с током, то согласно выражениям (6.1) и (6.2) для всех контуров отношение будет одно и то же (здесь М_max – максимальный вращающий момент).

Отношение

(6.3)

служит характеристикой магнитного поля, называемой магнитной индукцией. Таким образом, магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с током, магнитный момент которой равен единице (р_m = 1) и направлен вдоль положительной нормали к рамке.

В каждой точке поля вектор имеет единственное значение и направление. Поэтому силовое магнитное поле так же, как и электрическое, изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора . Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции. Густота линий магнитной индукции определяет в данной точке числовое значение магнитной индукции на единицу площади. Если приписать величине размерность В, то

(6.4)

В качестве примера на рис. 6.2 соответственно показаны линии магнитной индукции полей прямого тока (а); кругового витка с током (б); соленоида (в) (равномерно намотанная на непроводящий цилиндрический каркас обмотка, по которой течет ток).

а б в

I

Рис. 6.2

Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Этим они отличаются от линий напряженности электростатического поля, которые всегда разомкнуты (начинаются на положительных и кончаются на отрицательных зарядах). Эксперименты с постоянными магнитами показывают, что, разрезая магнит на части, невозможно разделить его полюса. У каждого отрезанного куска появляется соответственно новый южный или северный полюс. Эти эксперименты отражают один из фундаментальных законов природы: существуют разноименные электрические заряды, которые всегда можно разделить, и не существует их магнитных аналогов. Из этого свойства и вытекают все различия между магнитными и электростатическими полями.

До сих пор мы рассматривали макроскопические токи, текущие в проводниках. Согласно гипотезе Ампера¹ (1802 г.), в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Эти микротоки создают магнитное поле и могут ориентироваться определенным образом под действием магнитного поля макротока, помещенного вблизи тела, т.е. при одном и том же токе и прочих равных условиях вектор в различных средах будет иметь различные значения. Магнитное поле микротоков описывается вектором напряженности . Для однородной изотропной среды векторы и связаны следующим соотношением

(6.5)

где  – магнитная проницаемость среды (безразмерная величина), показывающая, во сколько раз магнитное поле макротока изменяется за счет поля микротоков среды; μ_о – магнитная постоянная:

Для магнитного поля, созданного несколькими макротоками (или движущимися зарядами), справедлив принцип суперпозиции, по которому магнитная индукция результирующего поля равна векторной сумме индукций , созданных отдельными токами

(6.6)

где i – число макротоков.

6.2. Закон Био–Савара–Лапласа

и его применение к расчетам магнитных полей

Результаты экспериментального изучения магнитных полей постоянных токов учеными были обобщены в выражении, называемом в их честь законом Био¹–Савара² –Лапласа³: элемент проводника с током I создает в некоторой точке А (рис. 6.3) индукцию магнитного поля , определяемую по формуле

(6.7)

где – вектор, по модулю равный длине элемента проводника и совпадающий по направлению с током I; – радиус-вектор, проведенный из элемента проводника в точку А поля.

Вектор (как и векторное произведение ) перпендикулярен к плоскости, в которой лежат векторы и . Направление также может быть найдено по правилу правого винта (см. рис. 6.3). В соответствии с формулой (6.7) модуль вектора определяется соотношением

(6.8)

где  – угол между векторами и .

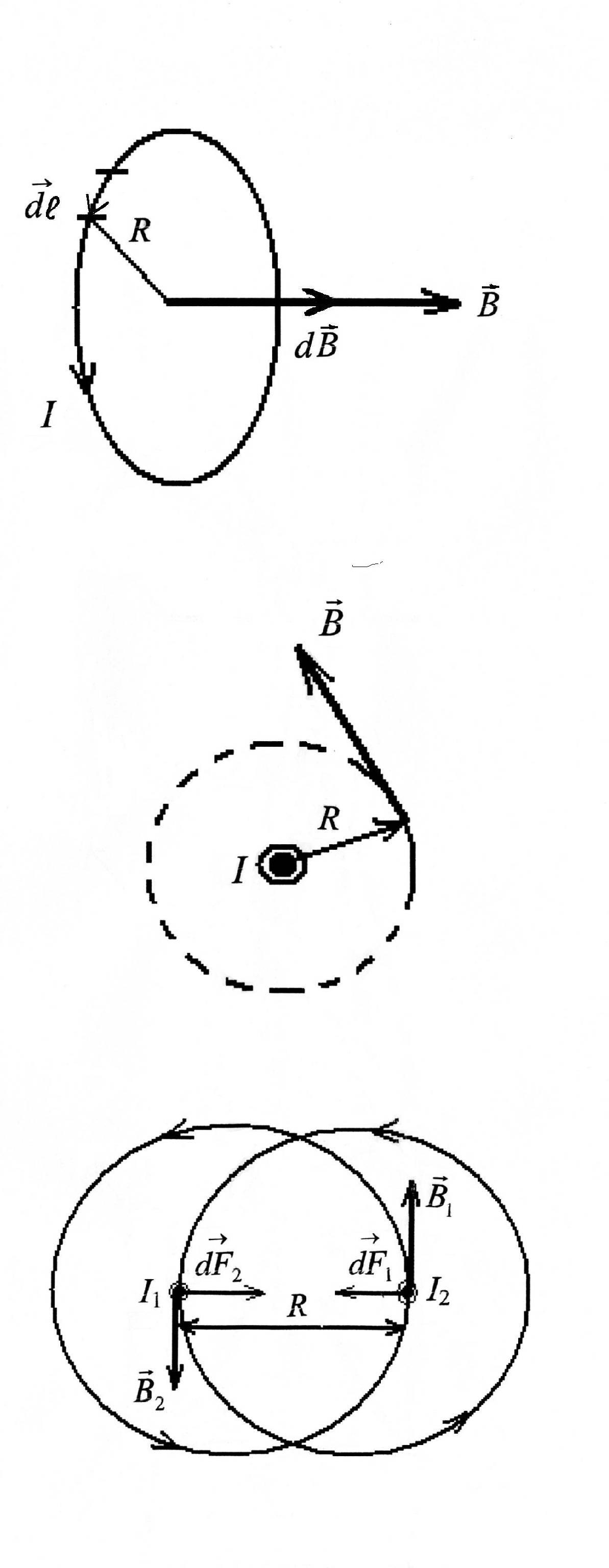
Рис. 6.3 Рис. 6.4

В общем случае расчет магнитных полей не так прост. Но для полей, обладающих определенной симметрией, применение соотношений (6.6), (6.7) и (6.8) существенно упрощается. В качестве примера рассмотрим расчет магнитного поля в центре кругового витка с током I (рис. 6.4).

Как следует из уравнения (6.7) и рис. 6.4, все элементы кругового витка с током создали в центре этого витка магнитное поле одинакового направления – вдоль нормали от витка, и сложение векторов по формуле (6.6) можно заменить сложением их модулей. Все элементы проводника перпендикулярны соответствующим радиусам-векторам (т.е. в уравнении (6.8) ); расстояние всех элементов кругового витка до центра одинаково и равно R. В итоге согласно уравнениям (6.8) и (6.6) для магнитной индукции в центре витка имеем

и

(6.9)

К началу

К следующей лекции К содержанию

К титулу

1 Х. Эрстед (1777–1851) – немецкий физик.

1 А. Ампер (1775–1836) – французский физик, математик и химик.

1 Ж. Био (1774–1862) – французский физик.

2 Ф. Савар (1791–1841) – французский физик.

3 П. Лаплас (1749–1827) – французский астроном, физик и математик.