Файловый архив студентов. Файловый архив студентов.
1306 вузов, 5172 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Московский государственный строительный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

17+Лекции+по+темеТеория+вероятности

.pdf
Скачиваний:
34
Добавлен:
03.03.2015
Размер:
1.3 Mб
Скачать
☆

~ 41 ~

 

 

 

 

 

 

 

t2

 

 

 

 

 

 

 

 

 

 

 

dz

 

 

 

 

 

 

 

 

e

t 2

 

 

Замена: z

dz tdt dt

V ez dz ez

2

 

 

 

 

z

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b

 

 

 

 

0

 

 

 

 

 

 

 

b

2

 

 

 

 

 

t2

 

 

t2

 

 

 

 

b

2

 

 

 

t2

 

 

t2

 

 

 

 

 

 

 

 

 

t e

 

 

 

e

 

dt

 

 

 

 

 

 

lim t e

 

 

 

lim t e

 

 

 

 

 

 

 

 

D(x)

 

 

2

 

 

2

 

 

 

 

 

2

 

 

2

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

b

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b2

 

 

 

 

 

 

 

 

lim

 

b

 

 

 

 

 

 

b2

 

 

2

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

e 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

lim

 

a

 

 

 

 

 

 

0

0

 

 

2

 

 

 

 

 

 

 

a

 

 

a2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

правило Лопиталя

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b2

 

 

1

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

lim

 

 

lim

 

 

 

2

 

 

 

 

b2

 

 

a2

 

 

 

2

 

 

 

 

b

 

 

a

 

 

 

 

 

 

 

 

 

b e

2

 

 

a e

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

0

 

 

 

 

 

D(x) b2

Средне квадратическое отклонение: b .

 

 

1

 

 

( x M )2

, x ( ; )

Окончательно имеем:

f (x)

 

e

2 2

 

 

 

 

 

 

 

 

 

 

2

 

 

 

Построение графика функции плотности распределения.

1.

x ( ; ) ;

 

 

 

 

 

 

 

 

 

 

 

 

 

2.

f ( x)

 

1

 

 

 

 

 

e

( x M )2

- общего вида;

 

 

 

 

 

 

 

2 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

e

M 2

 

3.

x=0;

f (0)

 

 

 

 

 

 

2b2

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M 2

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

A 0,

 

 

 

 

 

 

 

e

 

 

 

- точка пересечения с осью ординат.

 

 

 

 

 

 

 

 

 

 

 

 

b

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f (x) 0 - с осью абсцисс точек пересечения нет.

4.

Точек разрыва нет.

 

 

 

 

 

С

~42 ~

5.Вертикальных асимптот нет

k lim

f (x)

 

1

lim

 

1

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

( x M )

 

 

 

x

 

x

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x e 2 2

 

 

 

 

 

 

 

 

b lim

f (x) k x

1

 

 

lim

 

 

 

 

 

1

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

 

( x M )

x

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x e

2 2

 

 

 

y 0 - горизонтальная асимптота.

 

 

 

 

1

 

 

 

 

 

( x M )2

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

( x M )2

 

y

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

6.

 

 

 

 

 

 

 

 

e

 

 

2

 

 

 

 

 

 

 

 

 

 

 

(x

M )

 

 

 

 

(x

M ) e

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

 

3

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y 0 x M критическая точка на экстремум.

 

 

 

y

 

 

 

 

1

 

 

 

 

 

 

( x M )2

 

 

 

 

 

 

 

 

 

 

( x M )2

 

 

 

 

 

 

(x M )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e

 

2 2

 

 

(x M ) e

 

2 2

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

1

(x M )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

( x M )2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 e

 

 

 

2 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

e

M 2

1

M 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y (М )

 

 

 

 

 

 

 

 

 

2 2

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

2

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в точке x M - функция имеет максимум.

 

 

 

 

 

 

 

 

 

 

 

7.

f (M )

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

- точка максимума.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B M ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8.y 0 1 (x M )2 0

2

(x M )2 2 ; x M x M

 

 

 

x M x M

 

 

 

 

1

 

 

 

 

 

 

 

 

 

M 2 M 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y (M 2 )

 

3

 

 

2

1

 

 

 

 

 

 

2

0 вогнутость

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y (M 2 ) 0 вогнутость

y(M )

 

 

 

 

1

 

 

 

 

 

 

1 0 выпуклость

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C, D

M ;

 

 

e 2

 

 

 

 

точки перегиба

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

С

~ 43 ~

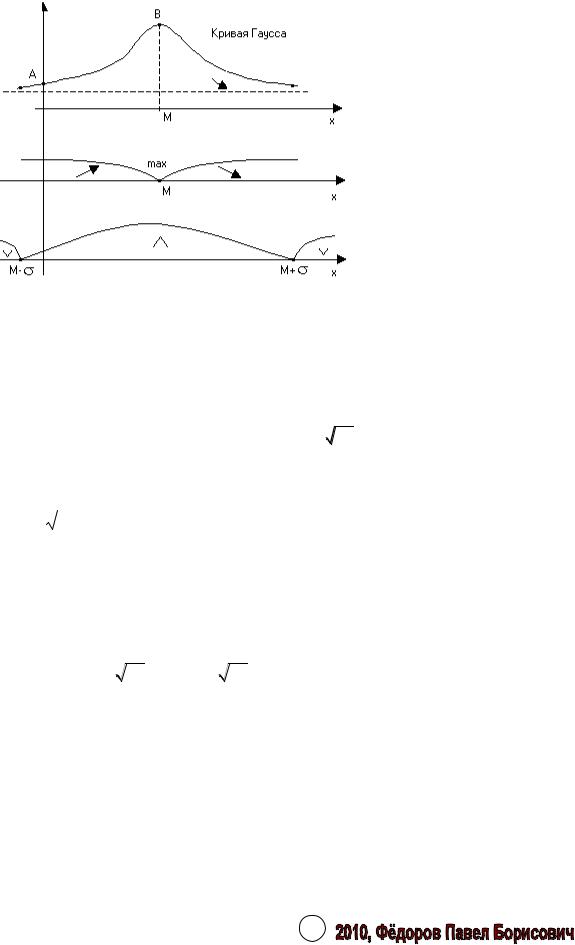
9. График

f (х)

Вероятность попадания в заданный интервал. Правило 3 для нормального распределения

b

1

 

 

b

( x M )

P(a x b) f (x)dx

 

 

e

 

 

 

 

2 2 dx

 

 

 

 

2

a

 

a

 

 

Существует функция Пуассона, которая вычисляется по формуле:

 

 

 

 

x

z 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ф(x)

 

1

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 dz

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

o

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

x M

dz

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Замена:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

M

 

 

 

 

 

b

M

 

 

 

 

 

 

 

 

 

dx dz z

 

 

; z

 

 

 

 

 

 

 

 

 

 

 

н

 

 

 

 

 

в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z2

 

 

 

 

 

 

 

 

 

 

b M

 

 

 

z2

 

 

a M

 

 

z2

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

в

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e

2 dz

 

 

 

 

2

dz

e

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e

 

 

 

dz

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

zн

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P(a x b) Ф b M

 

a M

 

Ф

 

 

 

С

~ 44 ~

Вычислим вероятность того, что отклонение случайной величины лежит

впределах данного допуска (дельта).

xM - отклонение

x M M x M

 

 

 

 

 

 

a

 

b

 

 

 

 

 

 

 

 

 

 

 

M M

 

M M

 

 

 

 

 

 

 

 

P(

x M

 

) Ф

 

 

Ф

 

 

 

Ф

 

Ф

 

 

2 Ф

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

P x M 3 2 Ф(3 ) 1

Правило 3 :

Для нормального распределения все возможные значения равные 1, лежат в следующем интервале: M 3 x M 3

Центральная предельная теорема Ляпунова

Терема: Если случайная величина представлена в виде суммы очень большого числа независимых случайных событий, влияние каждой из которой на сумму ничтожно мало, то такая случайная величина имеет распределение близкое к нормальному.

Замечание: Суммарная ошибка измерений и является такой случайной величиной.

С

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности