Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

РГР

.pdf

Скачиваний:

Добавлен:

03.03.2015

Размер:

442.62 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

		11
Составим условия равновесия:
n
kX		RAX+RBX+P1¡P2+P4 cos ®+Q1 sin ®¡Q2 = 0;
Fkx = 0;		RAX+RBX+P1¡P2+P4 cos ®+Q1 sin ®¡Q2 = 0;	(1)
=1
n
kX		RAY +RBY ¡P3¡P4 sin ®+Q1 cos ®¡P5 = 0;
Fky = 0;		RAY +RBY ¡P3¡P4 sin ®+Q1 cos ®¡P5 = 0;	(2)
=1	= 0;	RBY ¢ 16 ¡ P1 ¢ 6 + P2 ¢ 3 ¡ P3 ¢ 4 ¡ P4 cos ® ¢ 3+
k=1 MAZ ³F~k´	= 0;	RBY ¢ 16 ¡ P1 ¢ 6 + P2 ¢ 3 ¡ P3 ¢ 4 ¡ P4 cos ® ¢ 3+
n
X		+Q1 cos ® ¢10¡Q1 sin ® ¢7:5¡P5 ¢12+Q2 ¢7¡M = 0:	(3)
		+Q1 cos ® ¢10¡Q1 sin ® ¢7:5¡P5 ¢12+Q2 ¢7¡M = 0:	(3)

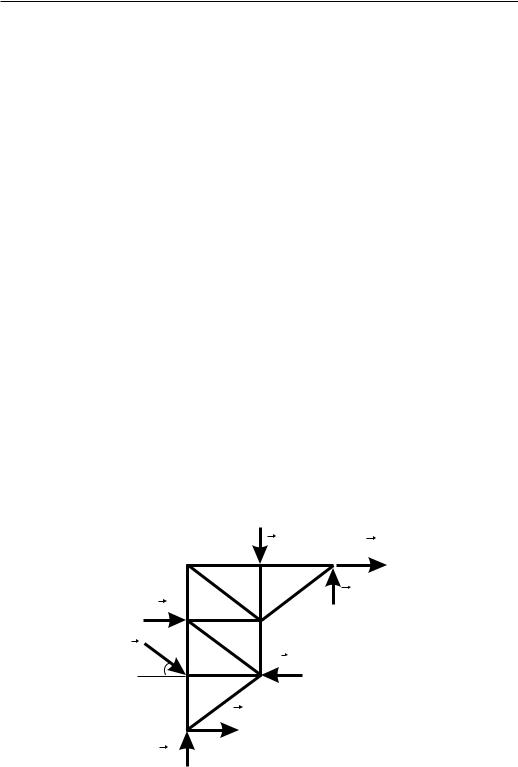
Рассмотрим равновесие левой части конструкции - фермы. Силовая схема представлена на Рис.3.

Составим условия равновесия:

n
kX		RAX+RCX+P1¡P2+P4 cos ® = 0;
Fkx = 0;		RAX+RCX+P1¡P2+P4 cos ® = 0;	(4)
=1
n
kX		RAY +RCY ¡P3¡P4 sin ® = 0;
Fky = 0;		RAY +RCY ¡P3¡P4 sin ® = 0;	(5)
=1	= 0;	¡RCX ¢9+RCY ¢8¡P1 ¢6+P2 ¢3¡P3 ¢4¡P4 cos ® ¢3 = 0:	(6)
k=1 MAZ ³F~k´	= 0;	¡RCX ¢9+RCY ¢8¡P1 ¢6+P2 ¢3¡P3 ¢4¡P4 cos ® ¢3 = 0:	(6)
n
X

		P3			RCY	P5
	D	P3	C	RCX	RCX	P5
	D		C	RCX	RCX
					C
3ì	P1			RCY	α			0.5ì
					α
					Q1			Q2
								Q2

3ì	P4					q1
3ì	P4
	α		P2					7ì
3ì						M		RBX
	A	RAX					B	RBX
	A	RAX					B
	RAY						RBY
							RBY

4ì

2ì

4ì

Ðèñ. 3

Ðèñ. 4

Рассмотрим равновесие правой части конструкции - пластины. Сило-

вая схема представлена на Рис.4.

Учитывая, что в соответствии с третьим законом Ньютона

¡!CX =

¡!CX;

!¡ CY

¡!CY

;

Получаем уравнения равновесия в виде:

¡RCX+Q1 sin ®¡Q2+RBX = 0;

Fkx = 0;

(7)

¡RCY +RBY ¡P5+Q1 cos ® = 0;

Fky = 0;

(8)

RBY ¢8+RBX ¢9¡P5 ¢4+Q1 cos ®¢2+

k=1 MCZ ³F~k´ = 0;

+Q1 sin ®¢1:5¡Q2 ¢2¡M = 0:

(9)

Определим составляющие реакций. Из уравнения (3) находим:

RBY = P1 ¢

¡ P2

+ P3 ¢

+ P4 cos ® ¢

¡ Q1

cos ® ¢

400

+Q1 sin ® ¢

+ P5 ¢

¡ Q2

+ M ¢

= 25 kH:

Из уравнения (2) находим:

RAY = ¡RBY + P3 + P4 sin ® ¡ Q1 cos ® + P5 = 15 kH:

Из уравнения (5) находим:

RCY = ¡RAY + P3 + P4 sin ® = 24 kH:

Из уравнения (6) находим:

RCX = RCY ¢

¡ P1

+ P2 ¢

¡ P3 ¢

¡ P4

cos ® ¢

= ¡8 kH:

Из уравнения (4) находим:

RAX = ¡RCX ¡ P1 + P2 ¡ P4 cos ® = ¡16 kH:

Из уравнения (7) находим:

RBX = ¡Q1 sin ® + Q2 + RCX = ¡14 kH:

Для проверки подставляем полученные результаты в неиспользованные уравнения (1), (8) и (9):

RAX + RBX + P1 ¡ P2 + P4 cos ® + Q1 sin ® ¡ Q2 = 48 ¡ 48 ´ 0;

¡RCY + RBY ¡ P5 + Q1 cos ® = 1 ¡ 1 ´ 0;

RBY ¢8+RBX ¢9¡P5 ¢4+Q1 cos ®¢2+Q1 sin ®¢1:5¡Q2 ¢2¡M = 264¡264 ´ 0:

Как видно, уравнения удовлетворяются тождественно. Следовательно, величины реакций определены верно. Таким образом:

RAX = ¡16 kH;	RBX = ¡14 kH;	RCX = ¡8 kH;
RAY = 15 kH;	RBY = 25 kH;	RCY = 24 kH:

Часть 2. Расч¨ет фермы.

Все внешние силы, приложенные к ферме, известны. Обозначим буквами все узлы фермы и цифрами - все е¨ стержни (Рис.5).

D				P3		C	RCX
		4	N				RCX
					12
					12
			5	10	13
				10			RCY
	3						RCY
P1		6
E				L
E			7
P4			7	11
	2			11
	2
α		8			P2
K				H
		9		H
	1	9
	1
A			RAX
A
RAY

Ðèñ. 5

Метод вырезания узлов.

Расч¨ет начинают с узла, соединяющего два стержня фермы. Затем переходят к соседним узлам в определ¨енной последовательности, которая позволяет на каждом шаге определять усилия в очередных двух стержнях. Первоначально предполагается, что стержни растянуты, т.е. их реакции направлены от узлов. Если усилие в каком–либо стержне оказывается отрицательным, то это означает, что данный стержень сжат.

Узел A

(Рис.6)

F e

= 0;

S9 cos ® + RAX = 0;

Fkye = 0;

S2 + S9 sin ® + RAY = 0:

Отсюда:

RAX

S9 = ¡

= 20; kH стержень растянут

cos ®

S1 = ¡RAY ¡ S9 sin ® = ¡27 kH:

стержень сжат

Узел K

(Рис.7)

Fkxe = 0;

S8 + P4 cos ® = 0;

S2 ¡ S1 ¡ P4 sin ® = 0:

Fkye = 0;

Отсюда:

S8 = ¡P4 cos ® = ¡12 kH;

стержень сжат

S2 = S1 + P4 cos ® = ¡18 kH:

стержень сжат

RAX

RAY

Ðèñ. 6

Ðèñ. 7

Узел H (Рис.8)

n
kX
Fkxe = 0;		S7	cos ® + S8 + S9 cos ® + P2 = 0;
=1
n
kX			S11 + S7 sin ® ¡ S9 sin ® = 0:
Fkye = 0;
=1
Отсюда:
S7 = ¡	S8	¡ S9	= ¡20; kH	стержень сжат
	cos ®
S11 = ¡S7 sin ® + S9 sin ® = 24 kH:				стержень растянут

Узел E

(Рис.9)

F e

= 0;

S6 + S7

cos ® + P1 = 0;

S3 ¡ S7

sin ® ¡ S2 = 0:

Fkye

= 0;

Отсюда:

S6 = ¡S7 cos ® ¡ P1 = ¡8; kH стержень сжат

S3 = S7 sin ® + S2 = ¡30 kH:

стержень сжат

S11

Ðèñ. 8

Ðèñ. 9

Узел D	(Рис.10)
	n
	kX
		Fkxe	= 0;	S4	+ S5 cos ® = 0;
	=1
	n
	kX
		Fkye	= 0;	S3	+ S5 sin ® = 0:
	=1
Отсюда:		S3
	S5 = ¡	S3	= 50; kH		стержень растянут

		sin ®
	S4 = ¡S5 cos ® = ¡40 kH: стержень сжат
Узел N	(Рис.11)
		n
		kX			S12 ¡ S4 = 0;
		Fkxe = 0;			S12 ¡ S4 = 0;
	=1
		n
		kX
		Fkye = 0;			S10 + P3 = 0:
	=1
Отсюда:	S12 = S4 = ¡40; kH				стержень сжат
	S12 = S4 = ¡40; kH				стержень сжат
	S10 = ¡3 = ¡30 kH:				стержень сжат

y				y
		S4	x	P3
D				P3
				S12
			S4		x
	α		S4
	α
				N
		S5
S3				S10
				S10

Ðèñ. 10

Ðèñ. 11

Узел L (Рис.12)

Fkxe = 0; S13 cos ® ¡ S5 cos ® ¡ S6 = 0;

k=1

Отсюда:

S5 =	S6	+ S5 = 40; kH	стержень растянут
	cos ®

Определены усилия во всех стержнях фермы. Оставшиеся уравнения равновесия узлов используем для проверки полученных результатов.

Fkye = 0; S10 + S13 sin ® + S5 sin ® = 54 ¡ 54 ´ 0:

k=1

S13

S10

S12

RCX

S13

RCY

S11

Ðèñ. 12

Ðèñ. 13

Узел C (Рис.13)

Fkxe = 0; RCX ¡ S12 ¡ S13 cos ® = 40 ¡ 40 ´ 0;

k=1

Fkye = 0; RCY ¡ S13 sin ® = 24 ¡ 24 ´ 0:

k=1

Метод сквозных сечений.

Провед¨ем сквозное сечение по третьему, шестому и одиннадцатому стержням. Рассмотрим равновесие нижней части фермы. Силовая схема представлена на Рис.14. Выбираем условия равновесия таким образом, чтобы в каждое из них входила только одна неизвестная.

k=1 MLZ ³F~k´	= ¡S4 ¢4¡P2 ¢3+P4 sin ®¢4+P4 cos ®¢3+RAX ¢6¡RAY ¢4 = 0:
n
X

							18
Отсюда	S3 = ¡30 kH:
	n		= S6 + P1 ¡ P2 + P4 cos ® + RAX = 0:
	=1	Fkxe	= S6 + P1 ¡ P2 + P4 cos ® + RAX = 0:
	kX
Отсюда	S6 = ¡8 kH:
n			= S11 ¢ 4 ¡ P2 ¢ 3 + P4 cos ® ¢ 3 + RAX ¢ 6 = 0:
k=1 MEZ ³F~k´			= S11 ¢ 4 ¡ P2 ¢ 3 + P4 cos ® ¢ 3 + RAX ¢ 6 = 0:
X
Отсюда	S11 = 24 kH:
y
S3				y
			S11	y
			S11
P1	S6	L
P1		L			P3
E					P3
E			S4	N	C	RCX	x
P4			S4	N			x
α	α		P2		α
α	α		P2
K		H		S10		RCY
		H		S10		RCY
A	RAX		x	L	S13
			x

RAY

Ðèñ. 14

Ðèñ. 15

Второе сквозное сечение провед¨ем через четв¨ертый, десятый и тринадцатый стержни (Рис.15).

k=1 MLZ ³F~k´		= S4 ¢ 4 + RCY ¢ 4 ¡ RCY ¢ 3 = 0:	Отсюда	S4 = ¡40 kH:
n
X
k=1 MCZ ³F~k´ = S10 ¢ 3 + P3 ¢ 3 = 0: Отсюда S10 = ¡30 kH:
n
X	³F~k	´ = ¡S13 sin ® ¢ 4 + RCY ¢ 4 = 0:
n
X			Отсюда
k=1 MNZ			Отсюда	S13 = 40 kH:

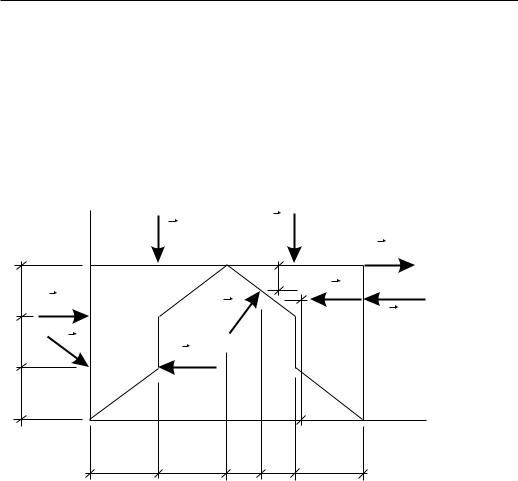
Построение диаграммы Максвелла–Кремоны.

На Рис.16 приведена разбивка на внешние и внутренние зоны действия сил.

						1	8
									Масштаб
									2kH
			P3				2, 13		3
			P3						3
	D	N		IV	C	RCX
	D	N			C
	III	XIII	XIV			7			6
		XIII	XIV		V
					V
P1	E	XII			RCY
			L	VI	RCY
	II	XI	L	VI		9
P4	II	XI				9	10, 14
	α	X	H	P2
	α			P2
	K	IX	VII					11	12
	I							11
	I
	A		RAX
		VIII

RAY

Ðèñ.16

Ðèñ.17

Диаграмма Максвелла–Кремоны приведена на Рис.17.

Таблица полученных результатов.

Метод	Усилие	S 1	S 2	S 3	S 4	S 5	S 6	S 7	S 8	S 9	S 10	S 11	S 12	S 13


Метод вырезания		-27	-18	-30	-40	50	-8	-20	-12	20	-30	24	-40	40
	узлов

Метод сквозных				-30	-40		-8				-30	24		40
	сечений

Диаграмма Максвелла-		-27	-18	-30	-40	50	-8	-20	-12	20	-30	24	-40	40
Кремоны

										20
Часть 3. Приведение системы активных сил к
простейшему виду.
	На Рис.19 изображена система активных сил, приложенных к рас-
			G1	G2
сматриваемой конструкции. Силы ¡!				и ¡! составляют пару сил с задан-
ным моментом MZ = ¡6 kH=м. Эту систему сил необходимо привести к
простейшему виду.
	y			P5
		P3		P5
		P3
	D		C		G 1
	D
				1.5 M			P1 = 24 kH;
3 M				1.5 M	G 2
3 M	P1				G 2		P2	= 12 kH;
			Q 1				P2	= 12 kH;

					Q 2		P3	= 30 kH;
					Q 2		P3	= 30 kH;
3 M	P4	P2		7 M			P4	= 15 kH;
		P2		7 M			P = 335			kH;
							P = 335			kH;
3 M							Q 1		= 40 kH;
	A				B	x	Q 2		= 18 kH;
							G 1		= 6 kH;
	4 M	4 M	2 M	2 M	4 M		G 2		= 6 kH.
			Ðèñ.19
	Графическое построение равнодействующей.

	На Рис.20 изображена в масштабе заданная система активных сил.
	P 0					P	G		Q0
Сила ¡!3 Представляет собой равнодействующую сил ¡!3							и ¡!1; сила ¡!2
			Q	G
- авнодействующая сил ¡!2				и !¡	2.
	Выбранная последовательность сложения сил следующая. Сначала
					P	P
строится равнодействующая сил ¡!2						и ¡!4; полученный результат скла-
	P		Q0			R
	P		¡!	- получаем силу ¡!1. Далее заменяем силы
дывается с ¡!1, затем с			2	- получаем силу ¡!1. Далее заменяем силы
P 0	Q						P
¡!3	и ¡!1 равнодействующей, которую складываем с силой ¡!5							- полу-
	R						R	R	2, то
чаем силу !¡		2. Оста¨ется построить равнодействующую сил ¡!1 и						!¡	2, то

!¡

есть равнодействующую F заданной системы активных сил.

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.2015816.17 Кб95РГР №7 Вариант №17.pdf
#
03.03.2015699.02 Кб30РГР №7 Вариант №17.pdf
#
03.03.2015807.99 Кб30РГР №7 Вариант №17.pdf
#
03.03.2015372.22 Кб85РГР- Баранникова Я.А.doc
#
03.03.2015108.42 Кб18РГР.docx
#
03.03.2015442.62 Кб45РГР.pdf
#
03.03.201558.37 Кб36Рек-Л2.doc
#
03.03.2015340.99 Кб49Рек-Л3.doc
#
03.03.201531.33 Кб46Рек. Л. 8.docx
#
03.03.201586.53 Кб45Рек. Л.9.doc
#
03.03.2015172.03 Кб119Рек.Л.4.doc

D				P3		C	RCX
		4	N				RCX
					12
					12
			5	10	13
				10			RCY
	3						RCY
P1		6
E				L
E			7
P4			7	11
	2			11
	2
α		8			P2
K				H
		9		H
	1	9
	1
A			RAX
A
RAY

D				P3		C	RCX
		4	N				RCX
					12
					12
			5	10	13
				10			RCY
	3						RCY
P1		6
E				L
E			7
P4			7	11
	2			11
	2
α		8			P2
K				H
		9		H
	1	9
	1
A			RAX
A
RAY

D				P3		C	RCX
		4	N				RCX
					12
					12
			5	10	13
				10			RCY
	3						RCY
P1		6
E				L
E			7
P4			7	11
	2			11
	2
α		8			P2
K				H
		9		H
	1	9
	1
A			RAX
A
RAY