
- •Статически определимые стержневые системы. Расчет статически определимых систем на неподвижную нагрузку.
- •2. Далее рассмотрим, как выглядит эпюра изгибающих моментов в консольной балке при приложенном на ее свободном конце сосредоточенном моменте m ( рис.19 ).
- •3. «Загрузим» консольную балку равномерно-распределенной нагрузкой q (рис.22). Заметим, что под ее интенсивностью q понимается нагрузка, приходящаяся на единицу длины балки. 1
- •Пример 2.
- •Пример 3.
- •Пример 4.
- •Пример 5.
- •Пример 6.
- •Пример 7.
- •Построение эпюр внутренних усилий в консольных рамах.
- •Пример 8.
- •Пример 8.
- •Построение эпюр внутренних усилий в трехшарнирных рамах.
- •Пример 9.
- •Пример 10.
- •X «от узла». Затем запишем уравнение, аналогичное примененному в случае с классической рамой, для определения одной из горизонтальных реакций:
- •Построение эпюр внутренних усилий в многопролетных статически определимых балках.
Пример 8.
4
2
2
2

Сначала пронумеруем границы характерных
участков. Обратим внимание на то, что
мы впервые сталкиваемся с трехстержневым
узлом 4. Наметим вначале последовательность
нашего расчета. Вначале рассмотрим
участок 1-2, затем перейдем на участок
2-4 и вычислим величину изгибающего
момента в сечении выше точки 4. Затем
рассчитаем участок 3-4 и вычислим момент
в сечении правее точки 4. Далее «вырежем»
узел 4 и определим величину момента
левее точки 4. В завершение расчета
рассмотрим участок 4-5. Расчет начинаем
с участка 1-2. Для этого вновь прибегнем
к уже ставшему стандартным приему –
мысленно установим в сечении, совпадающем
с окончанием первого участка, жесткую
заделку (рис.49,а). При этом эпюра на
участке 1-2 является аналогом первого
частного случая (см. рис.18), ее характер
и величина изгибающего момента левее
точки 2 известны (рис.49,б).
- 33 –
Для перехода на вертикальный участок 2-4 необходимо «уравновесить» узел 2, т.е. добиться, чтобы сумма моментов, как внутренних, так и приложенных снаружи внешних (если они есть), относительно оси узла 2 была бы равна нулю. Для этого «вырежем» узел 2 с помощью замкнутого сечения, приложим к нему известный момент в сечении левее точки 2, равный 6, растягивающий верхние волокна, что следует из рис.49,б, и вращающий узел против часовой стрелки, и внешний момент 10. Искомый момент M2Н в сечении ниже точки 2 в этом случае равен 10-6=4, вращает узел против часовой стрелки (рис.49,в). Обратим внимание на тот факт, что полученный из равновесия узла 2 момент, равный 4, растягивает левые волокна на стойке 2-4.
На следующем стандартном шаге ликвидируем условную заделку левее сечения 2 и переставим ее в сечение выше точки 4 (рис49,г). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2-4. Приложим к нему сосредоточенный момент М=4, полученный из равновесия узла 2 и растягивающий левые волокна. Это аналог случая 2 на рис.21, а эпюра на этом участке показана на рис.50,а. На участке 3-4 эпюра аналогична первому частному случаю (рис.18), а величина момента, растягивающего верхние волокна в сечении правее точки 4 равна М4П=5×2=10 (рис.50,б).

Рис.50
Для перехода на участок 4-5 необходимо «уравновесить» узел 4, т.е. добиться, чтобы сумма моментов относительно оси узла 4 была бы равна нулю. Для этого «вырежем» узел 4 с помощью замкнутого сечения, приложим к нему известные моменты в сечениях правее и выше точки 4 , равные, соответственно,10 и 4. Оба они вращают вырезанный узел по часовой стрелке. Искомый момент M4Л в сечении левее точки 4 в этом случае равен 4+10=14, вращает узел против часовой стрелки (рис.50,в). Обратим внимание на тот факт, что полученный из равновесия узла 4 момент, равный 14, растягивает верхние волокна.
Далее рассмотрим участок 4-5. Приложим к нему сосредоточенный момент М=14, полученный из равновесия узла 4 и растягивающий верхние волокна, в точке 4 приложим также сосредоточенные силы Р1=3 и Р2=5, перенесенные с участков 1-2 и 4-3, параллельных расчетному и рассмотренных ранее и равномерно-распределенную нагрузку q=3. Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 5. Независимое действие сосредоточенного момента М=14 соответствует частному случаю 2 (стр.21), приводя к растяжению верхних волокон. Отложим ординату выше нейтральной оси (рис.50,г). Воздействие равномерно-распределенной нагрузки на участок 4-5 приводит к возникновению изгибающего момента, растягивающего нижние волокна (по третьему частному случаю) и равного М=q×L2/2=3×42/2=24. Суммарное воздействие двух сосредоточенных сил приводит к растяжению верхних волокон, а вызванный ими изгибающий
- 34 -
момент равен (3+5)×4=60. Алгебраическая
сумма воздействий (в данном случае
изгибающих моментов) в заделке 5 равна
М5=74-24=50. Этот момент растягивает
верхние волокна. В пределах характерного
участка 4-5 эпюра изгибающих моментов
должна быть очерчена по квадратной
параболе с выпуклостью вверх. Результат
проведенного расчета на участке 4-5 ( без
уточнения поведения эпюры на этом
участке) – на рис.51,а. На рис.51,б показан
процесс построения эпюры Q на участке
4-5. На участке 4-5 на эпюре Q происходит
изменение знака, что указывает на наличие
экстремума на эпюре М. На рис.51,в приведены
полные эпюры изгибающих моментов и
поперечных сил для рассматриваемой
задачи.
Построение эпюры продольных сил начнем,
вырезав узел 2 с эпюры Q.
На рис. 52,а показан узел 2 с приложенными
к его стержням положительно направленными
искомыми продольными силами N2-1 и
N2-4, известными и
направленными в соответствии со знаками
поперечными силами левее и ниже этого
узла. Из уравнений равновесия получены
величины и знаки искомых продольных
сил. Далее вырезаем узел 3. При этом
обратим внимание на тот факт, что на
участке 3-4 в сечении 3 отсутствует
продольная нагрузка, что указывает со
всей очевидностью на отсутствие на этом
участке продольной силы. На рис.52,б
рассматривается узел 4 с приложенной
искомой продольной силой N4-5,
известной сжимающей продольной силой
N2-4=3, направленной «к узлу»,
поперечными силами левее, правее и выше
этого узла. Из уравнения равновесия
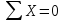 получены величина искомой продольной
силы. На рис.52,в можно ознакомиться с
эпюрой продольных сил для рассмотренного
примера.
получены величина искомой продольной
силы. На рис.52,в можно ознакомиться с
эпюрой продольных сил для рассмотренного
примера.
- 35 –



