2.1.2. Расчет сжатой глубины

Глубину потока в сжатом сеченииh_cвычисляем методом последовательных приближений (итераций ) по формуле

где ϕ - коэффициент скорости, определяемы по формуле

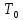- полный запас удельной энергии потока перед водосливной плотиной относительно дна водобоя

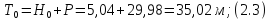
- критическая глубина

здесь коэффициент Кориолиса принят равным α = 1,05.

Отсюда согласно формуле (2.2) находим

В первом приближении в право части формулы (2.1) принимаемh_c= 0, тогда

Подставляя полученное значениев правую часть (2.1), определяем сжатую глубину во втором приближении

Вычисляем невязку между вторым и первым приближениями

Так как невязка составляет менее 3% принимаем сжатую глубину, равнойh_c = h_c⁽²⁾=0,821 м.

2.1.3. Расчет нормальной глубины

Глубину потока при равномерном теченииh0( нормальную глубину ) определяем методом Бахметева, согласно которому имеют место следующие соотношения между расходными характеристиками и глубинами в русле

где X- гидравлически показатель русла;K₁ иK₂- расходные характеристики, вычисляемые по формуле

при глубинах h₁иh₂;здесь и далее индексiпринимает значения 1 или 2 соответственно приh₁иh₂

Замечая, что площадь поперечного (живого ) сечения потока ω_i, смоченный периметр χ_i, гидравлически радиусR_iи коэффициент ШезиC_i определяются равенствами

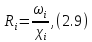
и принимая h₁=h_K = 3,56 м иh₂=h₀ = 5,7 м, последовательно находим

Отсюда, следуя (2.5), гидравлически показатель русла будет равен

при этом нормальная глубина потока составит

Сопоставляя полученное уточненное значение нормально глубины с найденным ранее по приближенной прямо формуле (1.8), равным h₀= 9,25 м, можно сделать следующие выводы :

- приближенная формула дает несколько заниженные значения нормально глубины,

- разность между приближенным и уточненным значениями составляет

т.е. 3%, что говорит о достаточно точности и применимости приближенной формулы (1.8) в инженерной практике, где допустимо считается погрешность до 5%.

Находим среднюю скорость потока воды в русле при нормально ( бытовой ) глубине и пропуске максимального расхода

Такая скорость течения в период половодий будет размывающей при связных и несвязных подстилающих грунтах, так как в этом случае V > V_доп.

Возможные мероприятия:

- искусственное крепление откосов и дня русла в зоне гидроузла,

- увеличение площади живого сечения потока за счет расчистки, расширения и углубления русла.

При скальных подстилающих породах расчетная скорость течения будет меньше допустимо (V < V_доп), при этом выполнение инженерных мероприятий по предотвращению размыва русла не потребуется.

2.1.4. Определение положения гидравлического прыжка и построение кривой свободно поверхности потока

Переход потока из бурного состояния в спокойное происходит в форме гидравлического прыжка при одновременном выполнении двух неравенств

Эти неравенства выполняются, поскольку согласно расчетам = 0,821 м, = 3,56 м и

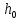= 5,86 м. Причемследовательно, в нижнем бьефе реализуется совершенный прыжок. Для заданного русла прямоугольного сечения раздельная глубина прыжка составит

Поскольку

то возникает отгон гидравлического прыжка

Вычислим глубину, сопряженную с бытовой

при которой реализуется прыжковый переход потока в нижнем бьефе из бурного в спокойное течение. При этом длина гидравлического прыжка составит

Кривую свободной поверхности будем строить по 5 промежуточным створам, разбив перепад высот кривой подпора на 6 равных доле с шагом по высоте

при этом глубина потока в створах начиная с i = 1 по 6 будет равна

Нулевым створом будем полагать створ сжатого сечения с глубиной,а шестым - створ с глубиной.

Расчет кривой подпора будем выполнять по уравнению Бахметева для неравномерного плавно изменяющегося движения жидкости в призматическом русле с положительным уклоном

где ,- глубины в конце и в начале расчетного участка длиной;η_i, η_i-1 - относительные глубины

j_ср- параметр Павловского

в котором C_cp - коэффициент Шези, определяемы по формуле Маннинга (2.10);i- уклон дна русла;R_cp, χ_cp- гидравлический радиус и смоченный периметр при

ϕ(η_i) и ϕ(η_i-1) - функции относительных глубин, принимаемые в данном случае равными ϕ(η_i) = η_i, поскольку для диапазонаη_iотдореализуется условие η_i<0,3. Для значений ϕ(η₅) и ϕ(η₆) производилась интерполяция между табличными значениями (с. 36-37, Приложение) при гидравлическом показателеX= 3,26.

Расчет интерполяции сведен в табл. 2.2.

Таблица 2.2

Расчет значений ϕ(η₅) и ϕ(η₆) при гидравлическом показателеX= 3,26

X=3,25				X=3,30
ϕ(ƞ5)	ƞ=0,3	ƞ=0,35	ƞ=0,303	ϕ(ƞ5)	ƞ=0,3	ƞ=0,35	ƞ=0,303
	0,301	0,352	0,304		0,301	0,352	0,304
		ϕ(ƞ5)	X=3,25	X=3,30	X=3,26
			0,304	0,304	0,304
X=3,25				X=3,30
ϕ(ƞ6)	ƞ=0,3	ƞ=0,35	ƞ=0,336	ϕ(ƞ6)	ƞ=0,3	ƞ=0,35	ƞ=0,336
	0,301	0,352	0,338		0,301	0,352	0,338
		ϕ(ƞ6)	X=3,25	X=3,30	X=3,26
			0,338	0,338	0,338

Расчет кривой подпора при отгоне гидравлического прыжка сведен в табл. 2.3.

Таблица 2.3

Расчет кривой свободно поверхности потока

№	, м	, м	ƞi-1	ƞi	hср, м	ωср, м2	χср, м
1	0,821	1,013	0,140	0,173	0,917	144,85	159,83
2	1,013	1,204	0,173	0,205	1,108	175,10	160,22
3	1,204	1,396	0,205	0,238	1,300	205,36	160,60
4	1,396	1,587	0,238	0,271	1,491	235,62	160,98
5	1,587	1,779	0,271	0,303	1,683	265,87	161,37
6	1,779	1,97	0,303	0,336	1,874	296,13	161,75
№	Rcp, м	Сср, м0,5/с	jcp	ϕ(ƞi-1)	ϕ(ƞi)	, м
1	0,906	39,35	0,1311	0,140	0,173	31,69
2	1,093	40,60	0,1392	0,173	0,205	32,63
3	1,279	41,67	0,1463	0,205	0,238	35,36
4	1,464	42,62	0,1527	0,238	0,271	36,91
5	1,648	43,47	0,1584	0,271	0,304	30,96
6	1,831	44,24	0,1637	0,304	0,338	33,44

Общая длина кривой подпора составит