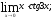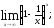§5. Предел промежуточной функции.


Изучите по учебнику Н.С.Пискунова §5,гл.2; §6, гл.2.
Рассмотрим функцию

Эта функция в точке
 не определена, тем не менее ее предел
при
не определена, тем не менее ее предел
при
 существует , причем
существует , причем

Этот предел часто называют первым замечательным пределом.
Пример 1.

Пример 2.
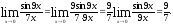
Пример 3.

Пример 4.

Пример 5.

Пример 6.
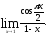
Сделаем замену
 ,
,
тогда при


4 случай. Раскрытие неопределенности типа 0·∞.
Пусть требуется найти
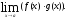
Если

то говорят , что произведение

представляет неопределенность 0·∞. Этот случай нахождения предела приводится к случаю 1 или 2 путем преобразования функции

Пример 7.

(см. пример 6).
Найдите пределы:
§6. Предел монотонной последовательности.
Число e и связанные с ним пределы.
Изучите по учебнику Н.С.Пискунова §5, гл.1; §5, гл.2, § 7-8, гл.2.
В высшей математике встречается несколько весьма важных пределов последовательностей. Одним из таких является предел последовательности

При
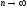 выражение, стоящее в скобках, стремится
к единице, а показатель степени , в
которую выражение в скобках возводится,
неограниченно увеличивается. Доказательство
того, что эта последовательность имеет
предел, основано на применении теоремы:
выражение, стоящее в скобках, стремится
к единице, а показатель степени , в
которую выражение в скобках возводится,
неограниченно увеличивается. Доказательство
того, что эта последовательность имеет
предел, основано на применении теоремы:
Всякая монотонная ограниченная последовательность имеет предел.
Предел последовательности по примеру Эйлера принято обозначать буквой e.
Итак,

Число e является иррациональным. Его приближенное значение с точностью до пятого знака: e≈2,71828.
Пример 1. Найдите

Решение. Сделаем замену


Рассмотрим теперь функцию

Число e ,определенное как предел последовательности , является также пределом этой функции при


Данный предел называется вторым замечательным пределом.
5 случай. Раскрытие неопределенности типа

Пусть требуется найти

Если


и

то говорят, что имеем неопределенность

В этом случае для нахождения предела используется второй замечательный предел. Вычисление многих пределов, связанных с числом e , основано также на применении следующего утверждения. Если
 то
то


Пример 2.

Пример 3.

Пример 4.

Найдите пределы:
Варианты контрольной работы.
Вариант 1.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 2.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 3.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 4.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
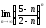 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 5.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 6.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 7.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)
Вариант 8.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
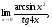 8)
8)
9)

Вариант 9.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 10.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 11.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6)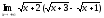 ,
,
7)
 8)
8)
9)

Вариант 12.
Вычислить пределы:
1)
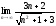 ,
2)
,
2)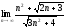 ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)

 8)
8)
9)

Вариант 13.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)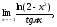
9)

Вариант 14.
Вычислить пределы:
1)
 ,
2)
,
2)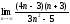 ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6)
7)
 8)
8)
9)

Вариант 15.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)
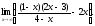
Вариант 16.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 17.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 18.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
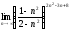 , 4)
, 4) ,
,
5)
 6)
6)
7)
 8)
8)
9)

Вариант 19.
Вычислить пределы:
1)
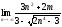 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 20.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)

6)
 ,
,
7)
 8)
8)
9)

Вариант 21.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 22.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 23.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4)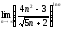 ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)
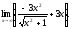
Вариант 24.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)

6)
 ,
,
7)
 8)
8)
9)

Вариант 25.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 26.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 27.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)

6)
 ,
,
7)
 8)
8)
9)

Вариант 28.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4)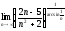 ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)
Вариант 29.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)

Вариант 30.
Вычислить пределы:
1)
 ,
2)
,
2) ,
,
3)
 , 4)
, 4) ,
,
5)
 6)
6) ,
,
7)
 8)
8)
9)