
ВВЕДЕНИЕ
Настоящие методические указания «Предел функции одной переменной» составлены применительно к программе курса высшей математики для студентов факультета промышленное и гражданское строительство.
Указания состоят из 6 параграфов, вариантов контрольных работ. Каждый параграф начинается с указания литературы, которую студент должен прочитать и усвоить. Затем следуют краткие теоретические сведения, которые необходимы для последующего решения задач. Далее приводятся решения «типовых» задач. В конце каждого параграфа предлагаются упражнения.
§1. Понятие предела функции.
Изучите по учебнику Н.С.Пискунова §6,гл.1; §2,гл.2.
Пусть
задана функция
 .
Теория пределов выясняет, как изменяются
значения функции при изменении аргумента
.
Теория пределов выясняет, как изменяются
значения функции при изменении аргумента .
.
Рассмотрим
поведение функции
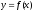
 около
точки
около
точки Предположим,
что функция определена в некоторой
окрестности точки
Предположим,
что функция определена в некоторой
окрестности точки ,за
исключением , быть может ,самой этой
точки. Пусть значения функции приближаются
к числу
,за
исключением , быть может ,самой этой
точки. Пусть значения функции приближаются
к числу ,когда
значения аргумента приближаются к
,когда
значения аргумента приближаются к Это записывается так:
Это записывается так: при
при
Тот факт,
что
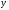 приближается
к
приближается
к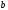 ,означает
, что разность
,означает
, что разность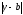 становится как угодно малой. А это в
свою очередь означает , что для любого
положительного
становится как угодно малой. А это в
свою очередь означает , что для любого
положительного
 наступит
такой момент в изменении
наступит
такой момент в изменении ,
после которого будет выполняться
неравенство
,
после которого будет выполняться
неравенство .
.
Процесс
изменения функции
 в
данном случае состоит в том , что
рассматриваются значения функции при
значениях аргумента
в
данном случае состоит в том , что
рассматриваются значения функции при
значениях аргумента ,
все более близких к
,
все более близких к и не равных
и не равных .Близкие
к
.Близкие
к значения
значения лежат в промежутке
лежат в промежутке ,где
,где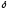 -
положительное число. Уменьшая
-
положительное число. Уменьшая ,
мы тем самым уменьшаем длину промежутка
,
мы тем самым уменьшаем длину промежутка и ограничиваемся рассмотрением все
более близких к
и ограничиваемся рассмотрением все
более близких к значений аргумента
значений аргумента .Для
.Для ,
лежащих в промежутке
,
лежащих в промежутке выполняются
неравенства
выполняются
неравенства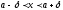 или
или
Последнее
неравенство записывается так:

Заметим,
что по свойству абсолютной величины
 при всех
при всех ,
причем
,
причем при
при и
и при
при
В теории
пределов рассматриваются значения
 близкие к
близкие к ,
но не равные
,
но не равные Чтобы исключить
Чтобы исключить из промежутка
из промежутка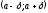 будем записывать
будем записывать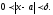
Утверждение
«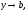 если
если »
означает, что для любого заранее
заданного числа
»
означает, что для любого заранее
заданного числа можно найти такой промежуток
можно найти такой промежуток
 что
для всех
что
для всех из этого промежутка,
из этого промежутка,
 выполняется
неравенство
выполняется
неравенство или
или
Число
 называется пределом функции
называется пределом функции при
при , стремящемся к
, стремящемся к ,
если для любого положительного числа
,
если для любого положительного числа существует такое положительное число
существует такое положительное число ,
зависящее от
,
зависящее от ,что
для всех
,что
для всех удовлетворяющих неравенству
удовлетворяющих неравенству выполняется неравенство
выполняется неравенство
В этом
случае пишут:

§2. Понятие предела последовательности.
Изучите по учебнику Н.С.Пискунова §3-5,гл.1; §1,гл.2.
Следует обратить внимание на то, что определение числовой последовательности является определением функции на множестве натуральных чисел, а поэтому определение предела последовательности сводится к определению предела функции на бесконечности.
Число
 называется пределом последовательности
называется пределом последовательности если для любого положительного числа
если для любого положительного числа ,
найдется такое число
,
найдется такое число зависящее
от
зависящее
от ,
что для всех членов последовательности,
номер которых
,
что для всех членов последовательности,
номер которых выполняется неравенство
выполняется неравенство
В этом
случае пишут:

Если последовательность имеет предел, то она называется сходящейся.
§3. Бесконечно малые и бесконечно большие; их свойства. Сравнение бесконечно малых.
Изучите по учебнику Н.С.Пискунова §3,4,11, гл.2.
Функция
 называется бесконечно малой при
называется бесконечно малой при если ее предел при
если ее предел при равен нулю, т.е.
равен нулю, т.е.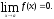
Аналогично
определяется бесконечно малая при

Отметим следующие свойства бесконечно малых.
Сумма любого конечного числа бесконечно малых при
 функций является бесконечно малой
функцией при
функций является бесконечно малой
функцией при
Пусть
 бесконечно
малая функция при
бесконечно
малая функция при а
а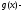 ограниченная функция в некоторой
окрестности точки
ограниченная функция в некоторой
окрестности точки .
Тогда произведение
.
Тогда произведение является бесконечно малой функцией
при
является бесконечно малой функцией
при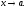
Функция
 называется
бесконечно большой при
называется
бесконечно большой при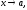 если для любого числа
если для любого числа найдется такое число
найдется такое число что для всех
что для всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
 ,
выполняется неравенство
,
выполняется неравенство
О бесконечно
большой функции говорят, что она стремится
к бесконечности или имеет бесконечный
предел и пишут:


Отметим следующую особенность терминологии: если функция имеет бесконечный предел, то это значит, что предел функции не существует.
Следует
обратить внимание, что из определения
бесконечно большой функции при
 следует, что знак
следует, что знак роли не играет, а требуется лишь , чтобы
абсолютная величина
роли не играет, а требуется лишь , чтобы
абсолютная величина могла быть сделана больше любого наперед
заданного положительного числа
могла быть сделана больше любого наперед
заданного положительного числа
Бесконечно большие функции обладают такими свойствами.
1). Сумма двух бесконечно больших функций одного и того же знака есть бесконечно большая функция того же знака.
2). Сумма бесконечно большой функции и ограниченной
функции – бесконечно большая функция.
3). Произведение двух бесконечно больших функций – бесконечно большая функция.
4). Произведение бесконечно большой функции на функцию, имеющую отличный от нуля предел,- бесконечно большая функция.
Между бесконечно большими и бесконечно малыми функциями существует тесная связь.
5). Если
 бесконечно большая функция при
бесконечно большая функция при , то
, то -
бесконечно малая функция при
-
бесконечно малая функция при .
Обратно, если
.
Обратно, если - бесконечно малая функция при
- бесконечно малая функция при ,
отличная от нуля в некоторой окрестности
точки
,
отличная от нуля в некоторой окрестности
точки ,за
исключением, быть может, самой точки
,за
исключением, быть может, самой точки то
то бесконечно большая при
бесконечно большая при
Отметим, что разность двух положительных бесконечно больших функций может быть бесконечно большой, бесконечно малой, постоянной или даже функцией , не имеющей предела.
