4. Краткие указания по технике безопасности

Работа с источниками ионизирующих излучений проводится в соответствии с Федеральными законами «О санитарно-эпидемиологическом благополучии населения» № 52-ФЗ от 30.03.99 г. и «О радиационной безопасности населения» № 3-ФЗ от 09.01.96 г., Нормами радиационной безопасности (НРБ-99), Основными санитарными правилами обеспечения радиационной безопасности (ОСПОРБ-99) и с другими нормативными документами.

При выполнении лабораторных, работ студентам запрещается:

- без надобности открывать крышку контейнера с источником иони­зирующего излучения и снимать его с рабочего места;

- держать без необходимости контейнер открытым (время работы с открытой крышкой контейнера должно строго соответствовать условиям проведения лабораторной работы);

- наклоняться над огражденным свинцом колодцем при находящемся там контейнере с источником ионизирующего излучения;

- в помещении лаборатории хранить и принимать пищу пользоваться косметикой.

Рекомендуется после окончания работы вымыть руки. Включение и выключение используемой в лабораторной работе аппа­ратуры производится лаборантом.

В случае неисправности аппаратуры необходимо обратиться к лабо­ранту или преподавателю, ведущему занятие.

5. Определение погрешностей при измерении интенсивности ионизирующего излучения

Эффективное использование на практике аппаратуры, регистрирую­щей излучение, тесно связано не только с хорошим знанием приборов и правил обращения с ними, но и с умением обработать и правильно записать результаты экспериментальных измерений.

Всякое измерение, как бы тщательно оно не было выполнено, обязательно сопровождается погрешностью (ошибкой), Погрешности обусловливаются разнообразными причинами (несовершенством измери­тельного прибора, влиянием окружающей среды, ошибкой эксперимен­татора и др.) и подразделяются на грубые, систематические и слу­чайные.

Грубые погрешности(промахи) возникают при небрежности, некомпетентности экспериментатора, неисправности прибора или резкого изменения условий измерений. Они легко обнаруживаются и исключаются из результата измерения на основании статистических методов.

Систематическими погрешностямиявляются те, причины которых известны и контролируемы, например, смещение шкалы прибора, отставание секундомера. Эти погрешности постоянны или изме­няются по известному закону при многократных измерениях одной и той же величины. Обычно эти погрешности исключают из результатов измерения, если их знак известен или включают в общую погрешность измерения, если их знак не известен.

Случайные погрешности связаны с неточностью отсчетов, которую совершенно непроизвольно может внести всякий экспериментатор, или с различными внешними воздействиями, не контролируемыми в процессе измерений. Случайные погрешности избежать не возможно. Они всегда изменяют результат измерений в меньшую или в большую сторону. Однако их можно уменьшить. Для уменьшения влияния случайных погрешностей на результат эксперимента измере­ния многократно повторяют, и результат измерений и его погрешность определяют по результатам многих отдельных измерений называемых наблюдениями.

Погрешности принято подразделять на абсолютные и относительные.

Абсолютные погрешностиΔхопределяются как разность между измереннымxи истиннымx_истзначением величины:

Δx = x – x_ист ( 5.1 )

Относительные погрешности δxопределяются как отношение абсолютной погрешности к значению истинной или измеряемой величины и выражаются в процентах:

( 5.2 )

Обработка результатов экспериментов осуществляется с использованием методов математической статистики.

Основными параметрами, которые использует математическая статистика, являются среднее, дисперсия, среднее квадратичное отклонение и коэффициент вариации.

Среднее (или среднее арифметическое) m наблюдаемых значений величины определяется по формуле:

( 5.3 )

Для генеральной совокупности среднее арифметическое называется математическим ожиданием или истинным значением измеряемой величины.

Дисперсия - это рассеяние случайной величины х_i относи­тельно математического ожидания. Для m значений величины х генеральной совокупности дисперсию определяют из выражения:

, (5.4)

где- отклонение (истинная абсолютная погрешность измерения величины) отдельного результата наблюденияот математического ожидания (истинного значения).

Для п значений величины х случайной выборки определяют величину выборочной дисперсии , как оценку дисперсии из выражения:

(5.5)

где- отклонение (оценка абсолютной погрешности измерения) отдельного результата наблюденияот среднего арифметического значения.

В формуле (5.5) в знаменателе стоит m-1, а не m потому, что среднее арифметическое для выборки отличается от среднего арифметичес­кого генеральной совокупности. Знаменатель определяют как число независимых наблюдений минус число тех связей, которые наложены на эти измерения при дальнейшей обработке материала.

Средним квадратичным отклонением и его оценкой называ­ют положительное значение корня квадратного из исоответственно. Его называют также стандартным отклонением, или просто стандартом.

Отношение среднего квадратичного отклонения к средней величине x, выраженное в процентах, характеризует относительную изменчивость результатов, называется коэффициентом вариации и обозначается v_x:

(5.6)

Для генеральной совокупности среднее арифметическое называетсяматематическим ожиданием или истинным значением измеряемой величины.

При регистрации параметров ионизирующих излучений случайные погрешности в значительной степени связаны с флуктуациями самой измеряемой величины и являются особой группой случайных погрешностей - статистическими погрешностями.

В результате экспериментов измеряют число импульсовN, зарегистрированных от источника за время по ко­торому определяют величину скорости счета , характеризующуюинтенсивность источника излучения.

Среднее (или среднее арифметическое) значениенаблюдаемых величин дляm измерений определяется по формуле:

( 5.7 )

Результаты отдельных наблюдений величин представляют собой последователь­ность дискретных величин N_i, отклонение которых относительно среднего арифметического значения описываетсяраспределением Пуассона по формуле:

, ( 5.8 )

Значения среднего квадратичного отклонения величин N_i и n_i, связанные с флуктуацией этих величин, оцениваются по формулам:

( 5.9 )

( 5.10 )

где определяется по форм. 5.3;

- средняя скорость счета импульсов из mнаблюдений.

Значения коэффициентов вариации, характеризующих относительную изменчивость и относительную погрешность результатов, определяются выражениями:

( 5.11 )

( 5.12 )

Из формул ( 5.9 ) - ( 5.10 ) следует, что значение среднего квадратичного отклонения величин N_i возрастает с ростом , а значение среднего квадратичного отклонения величин n_i возрастает с ростом и уменьшается с увеличением времени измерения. Коэффициент вариации величины N_i уменьшается с увеличением величины . Коэффициент вариации величинn_i уменьшается с увеличением величин и .

В случае соответствия распределения результатов наблюдения распределению Пуассона при отсутствии значимых других случайных погрешностей и отсутствии значимых или исключении систематических погрешностей вычисленные из результатов наблюдений значения средних квадратических отклонений должны наблюдаться приближенные равенства:

( 5.13 )

( 5.14 )

где и- средние квадратические отклонения при определении величини, определяемые по формулам:

( 5.15 )

( 5.16 )

Фактически эти равенства могут не выполняться при наличии значимых других случайных погрешностей и наличии не исключенных систематических погрешностей.

В случае, если независимо от того, соответствует или не соответствует распределение результатов распределению Пуассона,доверительные границы величин измерения ипри исключении всех систематических погрешностей будут определяться по формулам:

( 5.17 )

( 5.18 )

где - величина, зависящая от величины доверительной вероятности Р и числа степеней свободыf=m-1, принимаемая по табл. 5.1.

В случае, если распределение результатов соответствует распределению Пуассона и , тодоверительные границы величин измерения ипри исключении всех систематических погрешностей будут определяться по формулам:

( 5.19 )

( 5.20 )

Таблица 5.1

Значения t_Р для различной доверительной вероятности Р

(двусторонний критерий)

Число степеней свобо­ды f = m-1	Доверительная вероятность Р
	0,50	0,80	0,90	0 , 95	0,98	0,99	0,999
1	1,000	3,078	6,314	12,700	31,821	63,657	630,620
2	0,810	1,886	2,920	4,303	6,965	9,925	31,600
3	0,705	1,638	2,358	3,182	4,541	5,841	12,940
4	0,741	1,533	2,132	2,776	3,747	4,604	8,010
5	0,727	1,476	2,015	2,571	3,365	4,032	0,860
6	0,718	1,440	1,943	2,447	3,143	3,707	5,960
7	0,711	1,415	1,895	2,365	2,998	3,499	5,410
8	0,700	1,397	1,860	2,306	2,896	3,355	5,040
9	0,703	1,383	1,833	2,262	2,821	3,250	4,780
10	0,700	1,372	1,812	2,228	2,764	3,169	4,590
11	0,097	1,363	1,796	2,201	2,718	3,1 06	4,490
12	0,690	1,356	1,782	2,179	2,681	3,055	4,320
13	0,694	1,350	1,771	2,160	2,050	3,012	4,220
14	0,693	1,345	1,701	2,145	2,624	2,977	4,140
15	0,691	1,341	1,753	2,131	2,602	2,947	4,070
10	0,690	1,337	1,746	2,120	2,583	2,921	4,020
17	0,689	1,333	1,740	2,110	2,567	2,898	3,960
18	0,688	1,330	1,734	2,101	2,552	2,878	3,920
19	0,688	1,328	1,729	2,093	2,539	2,861	3,880
20	0,687	1,325	1,725	2,086	2,528	2,845	3,850
21	0,686	1,323	1,721	2,080	2,518	2,831	3,820
22	0,686	1,321	1,717	2,074	2,508	2,819	3,790
23	0,685	1,319	1,714	2,009	2,500	2.807	3,770
24	0,685	1,318	1,711	2,064	2,492	2,797	3,740
25	0,684	1,316	1,708	2,060	2,485	2,787	2,720
26	0,684	1,315	1,706	2,056	2,479	2,779	3,710
28	0,683	1,313	1,701	2,048	2,467	2,763	3,670
30	0,683	1,310	1,697	2,042	2,457	2,750	3,650
120	0,676	1,289	1,658	1,980	2,358	2,617	3,370
	0,674	1,282	1,615	1,960	2,326	2,576	3,290

где - величина, зависящая от величины доверительной вероятности Р, принимаемая по табл. 5.2.

Таблица 5.2.

Зависимость значения от величины доверительной вероятности Р

Р	0,95	0,96	0,97	0,98	0,99	0,995	0,999	10-6	10-7
u	1,96	2,054	2,17	2,325	2,576	2,612	3,291	4,417	5,327

В случае, если распределение результатов не соответствует распределению Пуассона и , тодоверительные границы величин измерения ипри исключении всех систематических погрешностей будут определяться по формулам:

( 5.21 )

( 5.22 )

При отсутствии реальных источников ионизирующих излучений счетчик может регистрировать импульсы частиц космических излучений, радиоизотопов, входящих в грунт и строительные материалы и других посторонних источников, определяющих так называемый фон счетчика. Наличие фона приобретает особенно большое значение при измерении интенсивности слабых источников и должно быть учтено в результатах измерения.

Скорость счета, обусловленная источником излучения и фоном, вычисляется по формулам

( 5.23 )

где - скорость счета источника излученияi-го наблюдения и средняя скорость счетаmнаблюдений за вычетом радиационного фона;

–то же вместе с радиационным фоном;

_ф– фоновая скорость счета.

В соответствии с формулой ( 5.23 ) погрешности результата измеренияопределяется выражением:

( 5.24 )

В соответствии с выражением ( 5.24 ) при увеличении количества наблюдений m и времени измерения даже при их неизменной точности погрешность измеряемой величины скорости счета n уменьшается. Однако влияние времени на величину погрешности наблюдается только в том случае, если распределение результатов наблюдения соответствует закону Пуассона, а влияние количества наблюдений имеет место всегда. В связи с этим наиболее надежным является увеличение количества наблюдений.

Используемые при определении погрешностей результатов измерений формулы основаны на предположении, что погрешности результатов наблюдений распределяются по нормальному закону (распределению Гаусса) или близкому к нему закону Пуассона. Однако это условие не всегда соблюдается. Поэтому при числе наблюдений m > 15 должна проводиться проверка на соответствие серии из m наблюдений предполагаемому закону распределения погрешностей.

При регистрации ионизирующих излучений достаточно проверить соответствие распределения результатов наблюдения распределению Пуассона. Наиболее удобно использовать проверку пo F - критерию. При этом для серии из m наблюдений величины п определяется опытное значение F - кри­терия F_оп по формуле:

( 5.25 )

где S_n - оценка величины среднего квадратического отклонения в серии из m наблюдений, определяемого по формуле ( 5.16 );

- среднее квадратическое отклонение, вычисляемое по формуле Пуассона ( 5.10 ).

Считается, что полученное из опыта распределение результатов наблюдения соответствует предполагаемому распределения при довери­тельной вероятности Р, если:

( 5.26 )

где - значениеF-критерия, принимаемое по величине доверительной вероятности Р и числу степеней свободы m-1 по табл. 5.3.

Таблица 5.3

Значения F_табл. F-критерия при различных значениях доверительной

вероятности Р и числа степеней свободы m-1

Р	Значения Fтабл. при различных значениях числа степеней свободы m-1
	1	2	3	4	5	6	10	12	24
0,95	3,8	3,0	2,6	2,4	2,2	2,1	1,9	1,8	1,5	1
0,99	6,6	4,6	3,8	3,3	3,0	2,8	2,5	2,2	1,8	1

В случае, если условие ( 5.26 ) соблюдается, то проверку соответствия распределения результатов наблюдений нормальному закону можно не проводить.

При проведении экспериментальных исследований перед каждым экспериментом составляется план, который включает:

- цель и задачи эксперимента;

- выбор варьируемых факторов;

- обоснование числа опытов;

- определение последовательности изменения факторов;

- обоснование средств измерений;

- описание проведения эксперимента;

- обоснование способов обработки и анализа результатов эксперимента.

- порядок реализации опытов;

При планировании эксперимента важным является определение минимального количества наблюдений, которое обеспечивало бы требуемую точность результата измерения.

В общем случае, при определении величины экспериментальных значений с требуемой погрешностью Δ_тр и заданной доверительной вероятностью Р необходимое количество наблюдений m_тр можно определить по формуле:

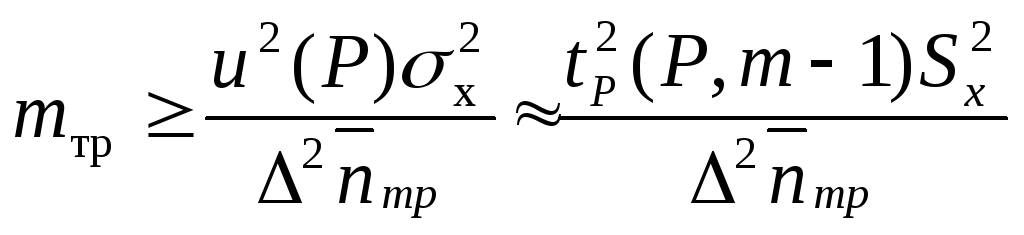( 5.27 )

где и- величины, принимаемые по табл. 5.1 и 5.2;

- дисперсия случайной величины n_i относи­тельно математического ожидания. Для m значений величины n генеральной совокупности дисперсию определяют из выражения:

, ( 5.28 )

где n_i – _{o =} Δn_o– истинная абсолютная погрешность отдельного измеренияn_i от среднего арифметического значения .

При регистрации параметров ионизирующих излучений, когда случайные погрешности в значительной степени связаны с флуктуациями самой измеряемой величины, определение необходимого минимального количества наблюдений имеет особенности.

Необходимое количество наблюдений m_тр для достижения требуемой величины погрешности Δ_тр или относительной погрешности δ_{тр =} Δ_тр/при заданной доверительной вероятности Р можно найти, если из предварительных измерений известны значения средних квадратических отклонений или оценкипри определении величины .

Значение m_тр определяется по формулам:

На основании полученных значений , ,,, заданной преподавателем требуемой относительной погрешностиδ_тр и доверительной вероятности требуемое число наблюденийm_трс учетом фона определяется по формулам:

Определив по формулам ( 5.31 ) и ( 5.32 ) требуемое количество измерений m_тр, проводим экспериментальные исследования при условии m_опт m_тр.

m_опт – оптимальное количество измерений.