10. Прочность изгибаемых железобетонных элементов по нормальным сечениям

10.1.Элементы прямоугольного сечения с одиночной арматурой

Высоту сжатой зоны определяют из выражения

.

Рис.10.1. Схема усилий и эпюра напряжений в поперечном прямоугольном сечении изгибаемого железобетонного элемента с одиночным армированием

Условия прочности

M < R_bbх(h₀ – 0,5x)

Можно также пользоваться выражением изгибающих моментов внутренней пары сил относительно ц.т. сжатой зоны

Задача 1 типа. Заданы размеры b и h. Необходимо определить площадь растянутой арматуры:

1 – определяют параметр

2 – по таблицам находят величины  и , при этом обязательно проверять условие

3- определяют площадь растянутой арматуры

Задача 2 типа. Требуется определить размеры сечения и армирования элемента.

1 – задаются из конструктивных условий шириной сечения b и требуемым значением относительной высоты сжатой зоны

2 – по таблице находят

3 – определяют требуемую высоту сечения

4 – определяют требуемую площадь сечения арматуры

10.2.Расчет по прочности нормальных сечений с двойной арматурой.

В практике проектирования часто встречаются случаи двойного армирования, т.е. установки в сжатую зону арматуры, хотя она там используется менее эффективно. Это производится в случаях для одиночного армирования при - низкая прочность бетона, недостаточная высота сечения. При этом сжатую арматуру должна раскреплять поперечная арматура.

Расчет прямоугольных сечений (рис.10.2) производится следующим образом в зависимости от высоты сжатой зоны

(10.1)

а) при - из условия

M < R_bbх(h₀ – 0,5x) + (h₀ – a’); (10.2)

б) при  > _R – из условия

M < _RR_bbh+ (h₀ - a'), (10.3)

где _R =_R(1 – 0,5_R).

Если прочность проверяют из условия

M  R_s A_s (h₀ – a'). (10.4)

Рис.10.2. Схема усилий и эпюра напряжений в поперечном прямоугольном сечении изгибаемого железобетонного элемента с двойным армированием

Изгибаемые элементы рекомендуется проектировать так, чтобы обеспечить выполнение условия  ≤ _R. Невыполнение этого условия можно допустить лишь в случаях, когда площадь сечения растянутой арматуры определена из расчета по предельным состояниям второй группы или принята по конструктивным соображениям.

Задача 1 типа. Определить площади сечения растянутой A_s и сжатой арматуры, соответствующие минимуму их суммы.

Учитывая, что площадь арматуры определяют по формулам:

(10.5)

A_s = _RR_bbh₀/R_s + , (10.6)

где _R и _R – определяются по зависимостям(см.формулу 3) .

Задача второго типа. Заданы размеры сечения b и h и площадь сжатой арматуры . Требуется определить площадь сечения растянутой арматуры. Определяют параметр

, (10.7)

.

Если _m < _R то площадь растянутой арматуры определится

.

Если _m > _R то сжатой арматуры недостаточно.

10.3.Тавровые и двутавровые сечения

Расчет сечений, имеющих полку в сжатой зоне (тавровых, двутавровых и т.п.), производят в зависимости от положения границы сжатой зоны:

а) если граница проходит в полке (рис.10.3,а), т.е. соблюдается условие

R_sA_s  R_b, (10.8)

расчет производят как для прямоугольного сечения шириной ;

б) если граница проходит в ребре (рис.10.3,б), т.е. условие (10.8) не соблюдается, расчет производят из условия:

Рис.10.3. Положение границы сжатой зоны в тавровом сечении изгибаемого железобетонного элемента

а - в полке; б - в ребре

, (10.9)

при этом высоту сжатой зоны определяют по формуле

, (10.10)

и принимают не более _Rh₀ .

Если x >_R h₀, условие (9) можно записать в виде

. (10.11)

Примечания: 1. При переменной высоте свесов полки допускается принимать значение , равным средней высоте свесов.

2. Ширина сжатой полки , вводимая в расчет, не должна превышать величин: при отсутствии поперечных ребер (или при расстояниях между ними, больших, чем расстояния между продольными ребрами) и при

в) при консольных свесах полки

при -

при

при - свесы не учитывают.

Требуемую площадь сечения сжатой арматуры определяют по формуле

, (10.12)

где A_ov = .

При этом должно выполняться условие . В случае, если, площадь сечения сжатой арматуры определяют как для прямоугольного сечения ширинойпо формуле (10.5).

Требуемую площадь сечения растянутой арматуры определяют следующим образом:

а) если граница сжатой зоны проходит в полке, т.е. соблюдается условие:

(10.13)

площадь сечения растянутой арматуры определяют как для прямоугольного сечения шириной ;

б) если граница сжатой зоны проходит в ребре, т.е. условие (10.13) не соблюдается, площадь сечения растянутой арматуры определяют по формуле

, (10.14)

где 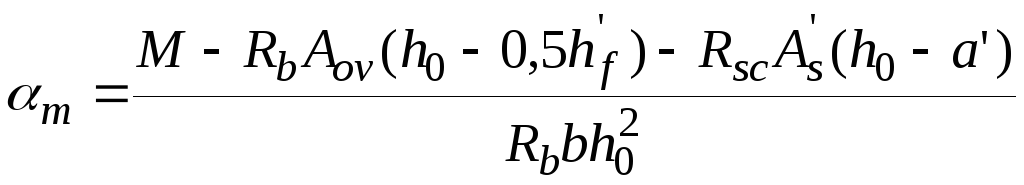.