4. Расчет и конструирование однопролетного ригеля.

Для опирания пустотных панелей принимаем сечение ригеля высотой h_b = 40 см.

4.1. Исходные данные.

Нормативные и расчетные нагрузки на 1 м² перекрытия принимаются те же, что и при расчете плиты перекрытия. Ригель шарнирно оперт на консоли колонны, h_b = 45 см.

Расчетный пролет:

l₀ = l_b – b– 2·20 – 130 = 5600 – 400 – 40 – 130 = 5030 мм = 5,03 м

где l_b – пролет ригеля в осях;

b – размер колонны.

Расчетная нагрузка на 1 м длины ригеля определяется с грузовой полосы, равной шагу рам, в данном случае шаг рам l_n = 6,4 м.

Постоянная (g):

- от перекрытия с учетом коэффициента надежности по ответственности здания γ_n = 1:

g_ƒl = g·l_n·γ_n = 471,3·6,4·1 = 3016,32 кг/м

- от веса ригеля:

g_bn = (0,2·0,40 + 0,18·0,2) ·2500 = 290 кг/м, где

2500 кг/м³ – плотность ж/б. С учетом коэффициента надежности по нагрузке γ_ƒ = 1,1 и по ответственности здания γ_n = 1,

g_b = 290·1,1·1 = 319 кг/м.

Итого постоянная погонная нагрузка, т.е. с грузовой полосы, равной шагу

g_l = g_ƒl + g_b = 3016,32 + 319 = 3335,32 кг/м.

Временная нагрузка (V₁) с учетом коэффициента надежности по отвественности здания γ_n = 1 и коэффициента сочетания

ψ_А1 = 0,4 + 0,6/ = 0,4 + 0,6/ = 0,701;

На коэффициент сочетания умножается нагрузка без учета перегородок:

V₁ = (V_p + ψ_А1·V₀)·γ_n·l_n = (64,8 + 0,701·195)·1·6,4 = 1289,57 кг/м

Полная погонная нагрузка:

g₁+V₁ = 3335,32 + 1289,57 = 4624,64 кг/м.

4.2. Определение усилий в ригеле.

Расчетная схема ригеля – однопролетная шарнирно опертая балка пролетом l₀. Вычисляем значение максимального изгибающего момента М и максимальной поперечной силы Q от полной расчетной нагрузки:

M = (g₁ + V₁)·/8 = 4624,64·5,03²/8 = 14625,94 кг·м;

Q = (g₁ + V₁)·l₀/2 = 4624,64·5,03/2 = 11630,97 кг;

Арматура продольная рабочая класса А500С диаметром 10-40 мм, R_s = 4350 кг/см², поперечная арматура А400 диаметром 6-8 мм, R_sw = 2900 кг/см²,

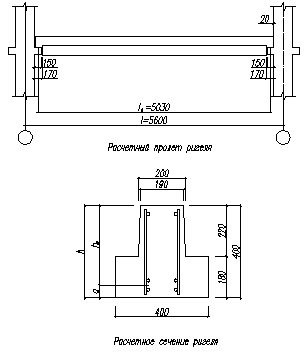
4.3. Расчет ригеля по прочности нормальных сечений при действии изгибающего момента.

Определяем высоту сжатой зоны x = ξ·h₀, где

h₀ – рабочая высота сечения ригеля;

ξ – относительная высота сжатой зоны, определяемая в зависимости от α_m.

h₀ = (h_b – 5) = 40 – 5 = 35 см,

α_m = M/(γ_b1·R_b·b·) = 1462594/(0,9·173·20·35²) = 0,383;

ξ = 1 - = 1 - = 0,516;

высота сжатой зоны x = ξ·h₀ = 0,516·35 = 18,07 см;

Граница сжатой зоны проходит в узкой части ригеля, следовательно, расчет ведем как для прямоугольного сечения.

Значение граничной относительной высоты ξ_R = 0,493. (Таблица 14 методички)

Площадь сечения растянутой арматуры определяется по формуле:

A_s = γ_b1·R_b·ξ·b·h₀/R_s = 0,9·173·20·0,516·35/4430 = 12,69 см²;

По найденной площади сечения растянутой арматуры по сортаменту подбираем 2Ø20 А500С и 2Ø22 А500С А_s,eƒ = 13,88 см²;

µ% = 13,88·100/(20·40) = 1,74 %

4.4. Расчет ригеля по прочности при действии поперечных сил.

Рабочая высота короткой консоли ригеля в подрезке h₀₁ = 20 см, вне подрезки (у опор) h₀ = 37 см, в средней части пролета h₀ = 35 см.

При диаметре нижних стержней продольной рабочей арматуры ригеля d_s = 22 мм с учетом требований п. 8.3.10 (СП 52-101-2003; 0,25·d_s = 5,0 ≈ 6 мм) назначаем поперечные стержни (хомуты) Ø8 А400. Их шаг на приопорном участке принимаем по конструктивным соображениям S_w1 = 10 см, что в соотвествии с п. 8.3.11 (СП 52-101-2003) не превышает 0,5h₀₁ = 0,5·20 = 10 см и 30 см.

Расчет ригеля по бетонной полосе между наклонными трещинами производятся из условия: Q ≤ φ_b1·R_b·b·h₀₁, где

φ_b1 – коэффициент, принимаемый равным 0,3. Проверка этого условия дает:

Q = 11630,97 кг ≤ 0,3·0,9·173·20·20 = 18684 кг,

следовательно принятые размеры сечения ригеля в подрезке достаточны.

Проверяем, требуется ли поперечная арматура по расчету, из условия:

Q ≤ Q_b,min = 0,5·R_bt·b·h₀₁,

т.е. Q = 11630,97 кг > Q_b,min = 0,5·0,9·11,7·20·20 = 2106 кг,

поэтому расчет поперечной арматуры необходим.

Находим погонное усилие в хомутах для принятых выше параметров поперечного армирования A_sw = 1,01 см² (2Ø8 А400), R_sw = 2900 кг/см², S_w1 = 10 см:

q_sw,1 = R_sw·A_sw/S_w1 = 2900·1,01/10 = 292,9 кг/см.

Q ≤ Q_b + Q_sw

c < 2·h₀₁ = 48 см. φ_b2 = 1,5 в соответствии с п. 6.2.34 (СП 52-101-2003).

Q ≤ 1,5·γ_b1·R_bt·b·/c + 0,75·q_sw·c;

Q > 1,5·0,9·11,7·20·20²/23,98 + 0,75·292,9·25,28 = 10537,2 кг,

условие прочности ригеля по наклонному сечению в подрезке при действии поперечной силы не соблюдается, следовательно уменьшим шаг поперечной арматуры:

A_sw = 1,01 см² (2Ø8 А400), R_sw = 2900 кг/см², S_w1 = 7 см:

q_sw,1 = R_sw·A_sw/S_w1 = 2900·1,01/7 = 418,43 кг/см.

Q ≤ Q_b + Q_sw

c < 2·h₀₁ = 48 см. φ_b2 = 1,5 в соответствии с п. 6.2.34 (СП 52-101-2003).

Q ≤ 1,5·γ_b1·R_bt·b·/c + 0,75·q_sw·c;

Q < 1,5·0,9·11,7·20·20²/20,07 + 0,75·418,43·20,07 = 12594,38 кг,

Следовательно условие прочности ригеля по наклонному сечению в подрезке при действии поперечной силы соблюдается.

Необходимо также убедиться в том, что принятый шаг хомутов S_w1 = 7 не превышает макисмального шага хомутов S_w,max , при котором еще обеспечивается прочность ригеля по наклонному сечению между двумя соседними хомутами:

S_w1 = 10 см < S_w,max = R_bt·b·h₀²/Q = 0,9·11,7·20·20²/11630,97 = 7,24 см.

Выясним теперь, на каком расстоянии от опор в соответствии с характером эпюры поперечных сил в ригеле шаг поперечной арматуры может быть увеличен. Примем, солгласно п. 8.3.11 (СП 52-101-2003), шаг хомутов в средней части пролета равным S_w2 = 0,75·h₀ = 0,75·35 = 26,25 = 26 см,что не превышает 50 см. Погонное усилие в хомутах для этого участка составляет:

q_sw,2 = R_sw·A_sw/S_w2 = 2900·1,01/26 = 112,65 кг/см.

Минимальная интенсивность усилия, при котором поперечная арматура учитывается в расчете:

q_sw,min = 0,25·R_bt·b= 0,25·11,7·20 = 58,5 кг/см.

Условия q_sw,1 = 418,43 кг/см > q_sw,min= 58,5 кг/см и q_sw,2 = 112,65 кг/см > q_sw,min = 58,5 кг/см выполняются.

При действии на ригель равномерно распределенной нагрузки q = g₁ + V₁ длина участка с интенсивностью усилия в хомутах q_sw,1принимается не менее значения l₁, определяемого по формуле: l₁ = (Q–Q_b,min)/q–c₁ и не менее l₀/4,

Q_b,min = 0,5·R_bt·b·h₀ = 0,5·11,7·20·35 = 4095 кг;

с₁ = = 71,34 см,

Так как с₁ < 2·h₀ = 90 см, то принимаем с₁ = 71 см; q = g + V = 46,25 кг/см, тогда:

l₁ = (11630,97 – 4095)/46,25 -80= 82,94 см.

Принимаем дополнительные хомуты у конца подрезки в количестве 2Ø12 А500С с площадью сечению А_sw,1 = 2,26 см², отгибы не используются. Проверка условия:

R_sw·A_sw,1 = 3060·2,26 = 6915,6 кг > Q·(1 – h₀₁/h₀) = 11630,97·(1 – 20/40) = 5815,49 кг,

следовательно дополнительных хомутов достаточно для предотвращения горизонтальных трещин отрыва у входящего угла подрезки.

Продольная арматура короткой консоли подрезки представлена горизонтальными стержнями, привариваемыми к опорной закладной детали ригеля, что обеспечивает ее надежную анкеровку на опоре, а значит и возможность учета с полным расчетным сопротивлением. Принимаем арматуру в количестве 2Ø12 А500С; А_s = 2,26 см²; R_s = 4430 кг/см.

Невыгоднейшее значение «с» определим по формуле:

с = (Q – R_sw·A_sw,1)/(q_sw,1 + q) = (11630,97 – 3060·2,26)/(418,43 + 46,25) = 10,16 см;

M = Q(a₀ + c) = 11630,97·(8,5 + 10,16) = 217033,9 кг·см = 2170,34 кг·м;

M_s = R_sA_sz_s = 4430·2,26·17 = 170200.6 кг·см = 1702,01 кг·м, при z_s = h₀₁ – a’ = 20 – 3 = 17 см;

M_sw = ΣR_swA_swz_sw = 0,5·q_sw,1·c² + R_swA_sw(c – a₁) = 0,5·418,43·10,21² + 3060·2,26·(10,16 – 3) =

= 71325,1 кг·см = 713,25 кг·м

Расчет по прочности наклонного сечения, проходящего через входяящий угол подрезки, на действие изгибающего момента производится из условия:

M ≤ M_s + M_sw + M_s,inc , M_s,inc = 0, т.к. отсутствуют отгибы.

Подставляем найденные значения в вышеописанное условие:

М = 2170,34 кг·м < М_s + M_sw = 1702,01 + 713,25 = 2415,26 кг·м,

следовательно прочность рассматриваемого наклонного сечения на действие изгибающего момента обеспечена.

Определим необходимую длину заведения продольной растянутой арматуры за конецподрезки по формуле:

w₀ = 2·(Q – R_sw ·A_sw,1)/q_sw + a₀ + 10d = 2·(11630,97 – 3060·2,26)/418,43 + 8,5 + 12 = 43,04 см,

w₀ = 43,04 < l_0,an = R_s·A_s/(R_bond·u_s) = 4430·1,131/(26,33·3,77) = 50,47

l_0,an– базовая (основная) длина анкеровки;

R_bond – расчетное сопротивление сцепления арматуры с бетоном

R_bond = η₁·η₂·R_bt = 2,5·1·11,7·0,9 = 26,33 кг/см².

Выясним необходимость устройства анкеров для нижнеготряда продольной арматуры ригеля. Для этого выполним расчет по прочности наклонного сечения, расположенного вне подрезки и начинающегося на расстоянии h₀ – h₀₁ = 37 – 20 = 17 см от торца ригеля, на действие изгибающего момента; тогда расстояние от конца анкеруемого стержня до рассматриваемого сечения l_s = 17 – 1 = 16 см.

При пересечении наклонного сечения с продольной растянутой арматурой, не имеющей анкеров в пределах зоны анкеровки, усилие в этой арматуре N_sопределяется по формуле:

N_s = R_s·A_s·l_s/l_an = 4430·6,28·16/84,12 = 5291,56 , где

l_an – длина анкеровки арматуры, равная l_an = λ_an·d_s = 42,06·2 = 84,12 см;

λ_an = R_s·α/(4·R_bond) = 4430·1/(4·26,33) = 42,06;

α – коэффициент, учитывающий влияние поперечного обжатия бетона в зоне анкеровки арматуры и при отсутствии обжатия принимаемый равным 1,0.

Учитывая, что в пределах длины l_s = 16 см к стержням нижнего ряда продольной арматуры приварены 2 вертикальных и 1 горизонтальный стержень Ø8 А400, увеличим усилие N_s на величину:

N_w = 0,7·n_w·φ_w·d_sw²·R_bt = 0,7·3·150·0,8²·11,7·0,9 = 2122,85 кг

Тогда σ_sA_s = N_s + N_w = 5291,56 + 2122,85 = 7414,41 кг.

Определим высоту сжатой зоны бетона (без учета сжатой арматуры):

x = σ_sA_s/(R_bb) = 7414,41/(0,9·173·20) = 2,38 см < 2·а’ = 6 см, т.е. z_s = h₀ – a’ = 37 – 3 = 34 см.

Невыгоднейшее значение «с» равно:

с = Q/(q_sw + q) = 11630,97/(418,43 + 46,25) = 25,03 см < w₀ – (h₀ – h₀₁) =

= 43,04 – (37 – 20) = 26,07 см,

т.е. при таком значении «с» наклонное сечене пересекает продольную арматуру короткой консоли. Принимаем конец наклонного сечения в конце указанной арматуры, т.е. на расстоянии w₀ = 43,04 см от подрезки, при этом с = 26,07 см.

Расчетный момент М в сечении, проходящем через конец наклонного сечения, равен:

М = Q(a₀ + w₀) – 0,5q(a₀ + w₀)² =

= 11630,97 (8,5 + 43,04) – 0,5·46,25·(8,5 + 43,04)² = 538031,6 кг·см = 5380,32 кг·м

Проверяем условие: M ≤ M_s + M_sw + M_s,inc, M_s,inc = 0:

М = 5380,32 кг·м > σ_sA_sz_s + 0,5q_swc² =

= 7414,41·34 + 0,5·418,43·26,07² = 394281,85 кг·см = 3942,82 кг·м.

Поскольку условия прочности по рассматриваемому наклонному сечению не соблюдается, необходимы дополнительные мероприятия по анкеровке концов стержней нижнего ряда продольной арматуры ригеля или устройство отгибов у входящего угла подрезки. Примем два отгиба из стержней Ø12 А500С сечением А_s,inc = 2,26 см², что позволяет создать дополнительный момент в наклонном сечении, равный:

М_s,inc = R_swA_s,incz_s,inc = 3060·2,26·42,55 = 294258,78 кг·см = 2942,59 кг·м

z_s,inc = z_scos(45˚) + (c – a₁)sin(45˚) = 34·0,707 + 26,18·0,707 = 42,55 см.

Проверка условия: M ≤ M_s + M_sw + M_s,inc :

М = 3942,82 кг·м < σ_aA_sz_s + 0,5q_swc²+ R_swA_s,incz_s,inc= 3942,82 + 2942,59 = 6885,41 кг·м

Таким образом, установка отгибов позволяет обсепечить соблюдение условия прочности по наклонному сечению вне подрезки.