4. Приближение функции. Интерполяция.

Процесс приближения функции находит широкое распространение не только в научной и технической областях деятельности человека, но и в его повседневной деятельности. Одним из видов приближения функции является интерполяция. Поэтому каждому студенту необходимо быть знакомым с основными методами и приемами интерполирования.

4.1 Постановка задачи приближения функции.

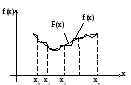
Пусть на отрезке [a,b] заданы точки х₀,х₁,…,х_n и значения некоторой функции f(x) в этих точках f(x₀)=y₀, f(x₁)=y₁,…,f(x_n)=y_n.

Необходимо построить такую функцию F(x), которая принимает в точках xi (i=0,1,2,…,n) значения, равные значениям f(xi): F(x0)=y0, F(x1)=y1, … , F(xn)=yn Такая функция F(x) называется интерполирующей, а точки x0, x1, …, xn – узлами интерполяции.

Интерполяционную функцию F(x) используют для вычисления значений функции f(x) в промежутках между точками x_i, x_i+1.

Процесс вычисления f(x) в промежуточных точках между x₀,x_n называется интерполяцией.

Наиболее часто встречается интерполяция многочленами

F_n(x) = a₀ + a₁x + a₂x² + … +a_nxⁿ

Для вывода формулы многочлена P_n(x) по заданным параметрам функции f(x) прежде всего введем понятие конечные разности функции.

4.2 Конечные разности различных порядков.

Рассмотрим случай равноотстоящих значений аргументов, т.е.

x_i – x_i-1 = h = const (i=1,2,…,n)

Величина h называется шагом.

Пусть известны значения функции в узлах xi

y_i = f(x_i)

Составим разности значений функции:

∆y₀ = y₁ – y₀ = f(x₀ + h) – f(x₀)

∆y₁ = y₂ – y₁ = f(x₀ + 2h) – f(x₀ + h)

… … … … … … … …

∆y_n-1 = y_n – y_n-1 = f(x₀ + nh) – f(x₀ + (n-1)h)

Эти значения называются первыми конечными разностями (или разностями первого порядка) функции. Аналогично составляются конечные разности второго порядка:

∆²y₀ = ∆(∆y₀) = ∆y₁ - ∆y₀; ∆²y₁ = ∆(∆y₁) = ∆y₂ - ∆y₁

Аналогично конечной разностью k-ого порядка будет:

∆^ky_i = ∆^k-1y_i+1 - ∆^k-1y_i; i=0,1,…,n–1

Конечные разности различных порядков удобно располагать в виде горизонтальной таблицы разностей.

Используя эти формулы, построим горизонтальную таблицу конечных разностей для n=5.

x	y	∆y	∆2y	∆3y	∆4y
x0 x1 x2 x3 x4	y0 y1 y2 y3 y4	∆y0 ∆y1 ∆y2 ∆y3	∆2y0 ∆2y1 ∆2y2	∆3y0 ∆3y1	∆4y0

Пример 3. Составить горизонтальную таблицу разностей функции

y = 2x³ – 2x² + 3x – 1

от начального значения x₀ = 0, приняв шаг h = 1.

РЕШЕНИЕ: Полагая x₀=0, x₁=1, x₂=2, x₃=3, находим соответствующие значения

y₀=–1, y₁=2, y₂=13, y₃=44

Эти значения запишем в таблицу:

x y ∆y ∆2y ∆3y 0 1 2 3 –1 2 13 44 3 11 31 8 20 12

Отсюда имеем ∆y0 = y1 – y0 = 3 ∆y1 = y2 – y1 = 11 ∆y2 = y3 – y2 = 31 ∆2y0 = ∆y1 - ∆y0 = 8 ∆2y1 = ∆y2 - ∆y1 = 20 ∆3y0 = ∆2y1 - ∆2y0 = 12

Рассматривая символ ∆ как оператор, можно указать следующие его свойства:

∆(u + v) = ∆u + ∆v

∆(C∙u) = C∆u

∆^m(∆ⁿu) = ∆^m+nu

∆⁰(u) = u

Конечные разности можно выразить непосредственно через значения функции

∆y₀ = y₁ – y₀

∆²y₀ = ∆y₁ - ∆y₀ = (y₂ – y₁) – (y₁ – y₀) = y₂ – 2y₁ + y₀

∆³y₀ = ∆²y₁ - ∆²y₀ = (∆y₂ - ∆y₁) – (∆y₁ - ∆y₀) = ∆y₂ – 2∆y₁ + ∆y₀ = (y₃ – y₂) – 2(y₂ – y₁) + (y₁ – –y₀) = y₃ – 3y₂ + 3y₁ – y₀

Аналогично для любого k в узле x₀ можно написать

∆^ky₀ = y_k – ky_k-1 + y_k-2 + … + (–1)^ky₀ (4.1)

Эту формулу можно записать и для значения разности в узле x_i:

∆^ky_i = y_k+1 – ky_k+i-1 + y_k+i-2 + … + (–1)^ky_i