3.3 Обратные матрицы
Матрица A-1 называется обратной по отношению к квадратной матрице A, если их произведение равно единичной матрице:
AA-1= A-1*A=E;
Всякая матрица с отличным от нуля определителем имеет обратную матрицу. При этом:
detA-1=
Минором элемента aij называется определитель (n1)-го порядка, образованный из определителя матрицы A зачеркиванием i-n строки из j-го столбца.
Алгебраическим дополнением Aij элемента aij называется его минор, взятый со знаком плюс, если сумма номеров i+j четная, и со знаком минус, если эта сумма нечетная.
Для квадратной матрицы третьего порядка после группировки слагаемых получим определитель ∆.
∆ =
= 
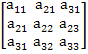Заключенные в скобках разности произведений элементов матрицы и есть алгебраические дополнения:
Aij=(-1)i+j ×Mij
А в целом это есть разложение определителя по первой строке матрицы, т.е.:
∆ =
Каждый
элемент обратной матрицы равен отношению
алгебраического дополнения 
исходной матрицы A
к знамению её определителя.
Таким образом, если detA = ∆ для этой же матрицы
=
=
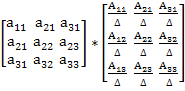=E
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
ЗАДАНИЕ 2
ДЕЙСТВИЯ С МАТРИЦАМИ
1) Вычислить произведение матриц A и B.
2)
Найти матрицу 
обратную матрице A.
Задания приведены в таблице 2.
ТАБЛИЦА 2
|
|
0,1,2 |
3,4,5,6 |
7,8,9 | |||
|
A |
B |
A |
B |
A |
B | |
|
0 1 |
5 8 1 1 2 3 2 –3 2 |
–1 0 5 0 1 3 2 –2 5 |
1 2 1 3 –5 3 2 7 –1 |
1 2 1 2 3 1 2 1 3 |
1 2 1 2 3 1 2 1 3 |
0 –2 6 2 4 3 0 –3 4 |
|
2 3 |
1 2 4 5 1 2 3 –1 1 |
0 2 3 1 0 –2 3 1 1 |
4 –3 2 2 5 –3 5 6 –2 |
2 3 1 4 –1 0 0 1 2 |
2 –1 –1 5 4 –2 3 –2 4 |
5 1 2 –1 2 0 1 0 1 |
|
4 5 |
5 3 –1 2 0 4 3 5 –1 |
1 1 2 2 –1 2 4 1 4 |
3 –1 0 –2 1 1 2 –1 4 |
–1 2 4 0 3 2 –1 –3 4 |
3 –1 1 2 –5 –3 1 1 –1 |
1 4 2 2 1 –2 0 1 –1 |
|
6 7 |
1 1 1 2 –1 –5 3 –2 0 |
4 2 1 3 –2 0 0 –1 2 |
2 1 –1 1 1 1 3 –1 1 |
1 0 3 –2 0 1 –1 2 1 |
2–1–3 3 4–5 0 2 7 |
2 3 1 –1 2 4 5 3 1 |
|
8 9 |
1 5 1 2 –1 –1 1 –2 –1 |
–1 –2 3 2 3 5 1 4 –1 |
1 –2 3 2 3 –4 3 –2 –5 |
2 3 1 4 –1 0 0 1 2 |
3 4 2 2 –1 –3 1 5 1 |
2 1 3 1 –2 0 4 –3 0 |
Вычислить сумму произведений одноименных элементов, аналогично рассчитывая остальные сij.
С11=
С12=
С13
=
С21=
С22=
С23=
С31=
С32=
С33=
Следовательно:
С=A*B=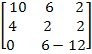
2. Найдем обратную матрицу A-1. Матрица
A=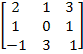
имеет обратную, если её определитель ∆
не равен нулю.
Вычислить определитель.
Для этого разложим его по первой строке матрицы A
∆=
Вычислим
алгебраические дополнения по формуле:
Минор
получают вычеркиванием i-й
строки и j-го
столбца матрицы A,
и из оставшейся части матрицы рассчитывается
определитель:
=(-1)1+1
=(-1)1+2
=(-1)1+3
Определитель
∆=
не равен 0, значит, матрица A
имеет обратную матрицу A-1.
Выражение обратной матрицы:
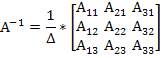
Здесь
-
алгебраическое дополнение элементов
матрицы A.
Так
как 
уже вычислены, то вычислим остальные
:
=(-1)2+1
=(-1)2+2
Подставим
в выражение для 
,
=(-1)2+3
=(-1)3+1
=(-1)3+2
=(-1)3+3
получим обратную матрицу:
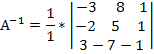
Для
матрицы A
и её обратной должно выполняться
равенство 
,
где E-
единичная матрица.
Перемножим
матрицы A
и 
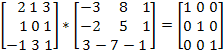
Обратная матрица определена верно.