3. Решение системы линейных

УРАВНЕНИЙ.

Система n уравнений от n неизвестных называется линейной, если неизвестные входят в неё только в первой, например:

a

(2.1)

₁₁x₁ + a₁₂x₂ + … + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n = b₂

_{……………………………………}

a_n1x₁ + a_n2x₂ + … + a_nnx_n = b_n

Здесь a_ij-коэффициенты уравнений;

x_i- неизвестные;

b_i- свободные члены уравнений (i,j=1,2..n).

Записывая коэффициенты этой системы a_ij в виде прямоугольной таблицы, а неизвестные x_i и свободные члены b_i в виде столбцов.

A= 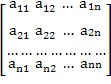, x= , b =

Систему уравнений (2.1) можно записать в векторно-матричном виде:

Ax=b

Здесь: A-матрица коэффициентов системы

x- вектор-столбец неизвестных

b- вектор-столбец свободных членов.

Так как алгебра матриц широко используется в теории линейных уравнений, рассмотрим ее основные понятия.

3.1 Основные понятия алгебры матриц.

Матрицей называется система m×n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов

A=

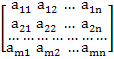
Если m=n, то матрицу называют квадратной порядка n. Прямоугольную матрицу типа m×n обозначают в виде A=[a_ij]_m×n.

Квадратная матрица вида

A=

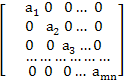
называется диагональной и обозначается A=[a₁ ,a_2,…,a_n].

Если a_i=1(i=1,2…,n), то матрица называется единичной и обозначается буквой E

E=

Матрица называется нулевой, если все ее элементы равны нулю. Она обозначается O_mn. Матрица называется верхней треугольной, если все элементы ее ниже главной диагонали равны нулю, и нижней треугольной, если ее элементы выше главной диагонали нулевые.

Матрица называется ленточного типа, если ненулевые элементы её располагаются параллельно главной диагонали, а остальные равны нулю.

Каждой квадратной матрице A соответствует определитель (детерминант), который обозначается detA или ∆.

Определители для матриц второго и третьего порядка вычисляются по правилу Саррюса:

∆ = detA = =

В этом случае определитель равен разности произведений элементов матрицы, расположенных вдоль главных диагоналей

Для вычисления определителя 3-го порядка к ней справа добавляются два первых столбца элементов, а затем составляется сумму произведений элементов, расположенных вдоль диагоналей, причем произведения элементов сверху вниз берутся со знаком плюс, а снизу вверх- со знаком минус.

detA = =

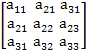3.2 Действия с матрицами

Если матрицы A и B одного типа, то имеет смысл операции сложения и вычитания.

Матрица суммы (разности), матриц A и B есть матрица C, элементы которой равны сумме (разности) соответствующих элементов матриц A и B.

Матрицу A можно умножить на число α. В результате получается матрица B, элементы которой получены умножением всех элементов матрицы A на число α.

Матрица –A=(–1)A называется противоположной матрице А. Если A-квадратичная матрица порядка n, то определитель матрицы C= αA равен:

detC = detαA = αⁿdetA

Операция умножения матриц:

Пусть A и B матрицы типов m×n и p×q соответственно. Если число столбцов n матрицы A равно числу строк p матрицы B(n=p), то для этих матриц существует матрица C типа m×q, являются их произведением.

C = ,

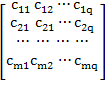где (i=1,2,…,m, j=1,2,…,q)

Т.е. элемент матрицы – равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B.

В общем случае AB ≠ BA. Если матрица A типа m×n и B типа p×q, то AB – матрица типа m×q, а BA – p×n.

Например:

A = ; B = ; AB =

BA = , т.е. AB ≠ BA;