2.3 Действия над приближенными

ЧИСЛАМИ.

При сложении и вычитании их абсолютные погрешности складываются.

При умножении и делении их относительные погрешности складываются.

Относительная погрешность степени или корня от приближенного числа равна относительной погрешности числа, умноженной на степень или деленной на показатель корня соответственно.

Для случая двух приближенных чисел а и b эти правила можно выразить математически:

∆(a±b)= ∆a±∆b;

δ

(2.1)

(a∙b)= δa+δb;

δ(a/b)= δa+δb;

δ(a_k)=k∙δa;

δ()=.

Во избежание завышения абсолютной погрешности суммы(разности) большого количества слагаемых, округленных до m-ого десятичного знака (т.е. их погрешности оцениваются величиной 0,5∙10^-m), абсолютная погрешность суммы (разности) оценивается правилом Чеботарева:

∆_s =∙ 0,5 ∙ 10^-m

n – число слагаемых.

Если среди слагаемых имеется одно число, абсолютная погрешность которого значительно превосходит погрешности остальных слагаемых, то абсолютная погрешность суммы (разности) считается равной этой наибольшей погрешности.

Пример 2.1

Найти сумму приближенные чисел 0,348; 0,1834; 345,4; 235,2; 11,75; 9,27.

Решение: наибольшую абсолютную погрешность ∆=0,05 имеют два числа 345,4 и 235,2. Поэтому можно считать, что абсолютная погрешность суммы составляет 2∆=0,10. Так как количество слагаемых невелико, то округляем слагаемые до 0,01

345,4 235,2 11,75 9,27 0,35 0,18	В окончательном результате последний знак отбрасывается: S=602,15 При этом к ранее определенной погрешности ∆s=0,10 добавляем погрешность округления 0,05, что дает ∆s=0,15, а округляя это число, получим ∆s=0,2
S=602,15

Т.о. полный учет всех погрешностей только усложнил бы расчет, не внося существенных уточнений в результат.

2.4 Погрешности вычисления значений функции.

Пример 2.2. Найти относительную погрешность функции

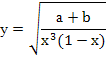
Используя формулы (2.1)

δy = [ δ(a+b) + 3δx + δ(1-x) ] =

Полученная оценка относительной погрешности содержит в знаменателе . Ясно, что при x≈1 можно получить завышенную погрешность. Поэтому при организации вычислительных алгоритмов следует избегать вычитания близких чисел, при возможности алгоритм надо видоизменить во избежание потери точности на некотором этапе вычисления.

Рассмотрим функцию одной переменной y=f(x). Пусть a – приближенное значение аргумента х. ∆а – его абсолютная погрешность. Абсолютную погрешность функции можно считать ее приращением, которое возникает при изменении аргумента на ∆а. это приращение можно заменить дифференциалом: ∆y≈dy. Тогда для оценки абсолютной погрешности получим выражение:

∆y=| f '(x) |∆a

Для функции нескольких аргументов. Например, оценка абсолютной погрешности функции U=f(x,y,z), приближенные значения аргументов, которой соответственно a,b,c имеет вид:

Здесь ∆a, ∆b, ∆c – абсолютные погрешности аргументов.

Относительная погрешность находится по формуле:

δU =

ПРИМЕР 2.3

Найти абсолютную и относительную погрешность объема шара.

Дано: d=3,7±0,05 см π=3,14+0,0016	Решение: V = ; = = 8,44 = = 21,5 ∆V= Поэтому V=26,5±1,1см3 ΔV= = 0,041 ≈ 4%
Найти: ∆V=?, δv=?

ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО

Определить абсолютную и относительную погрешности объема параллелепипеда, имеющего стороны:

a=5±0,05см

b=7±0,05см

с=4±0,02см

Решение:

V=a*b*c=140см²