8. Приближенное решение обыкновенных дифференциальных уравнений.

Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции y=y(x)

F(x,y,y¹,…,y⁽ⁿ⁾) = 0, где x-независимая переменная.

Решением дифференциального уравнения называется функция, которая после её подстановки в уравнение превращает его в торжество.

Некоторые методы решения известны по курсу дифференциальных уравнений. Для ряда уравнений первого порядка ( с разделяющимися переменных однородных, линейных и др) удается получить решение в виде формул путем аналитических преобразований.

В большинстве случаев для решения дифференциальных уравнений используются приближенные методы, которые можно разделить на две группы:

1)аналитические методы, дающие решение в виде аналитического выражения;

2)численные методы, дающие приближенное решение в виде таблицы.

Рассмотрим перечисленные методы в виде следующих примеров.

8.1 Метод последовательного дифференцирования.

Рассмотрим уравнение:

с начальными условиями , где – заданные числа.

Предположим, что искомое решение y=f(x) может быть решено в ряд Тейлора по степеням разности (x-x₀):

²ⁿ+….

Начальные условия (8.2) дают нам значения y^(k)(x₀) при k=0,1,2,...,(n-1). Значения y⁽ⁿ⁾(x₀) найдем из уравнения (8.1), подставляя (x-x₀) и используя начальные условия (8.2):

y⁽ⁿ⁾(x₀) = f(x₀,y₀,y^'₀,...,y₀^(n-1))

Значения y⁽ⁿ⁺¹⁾(x₀), y⁽ⁿ⁺²⁾(x₀)... последовательно определяются дифференцированием уравнение (8.1) и подстановкой x=x₀, y^(k)(x₀)=y_0k (k – 0,1,2).

ПРИМЕР: Найти первые семь членов разложения в степенной ряд решения y=y(x) уравнения y^''+0,1(y^')²+(1+0,1x)y=0 с начальными условиями y(0)=1; y^'(0)=2.

РЕШЕНИЕ: Решение уравнения ищем в виде ряда:

y(x)=y(0)+y'(0)x/1!+y''(0)x²/2!+...+y⁽ⁿ⁾(0)xⁿ/n!...

Из начальных условий имеем y(0)=1, y^'(0)=2. Для определения y^''(0) разрешим данное уравнение относительно y'':

y''(0)= – 0,1(y^')² – (1+0,1x)y (8.3)

Используя начальные условия, получим

y''(0)= –0,1*4 – 1*1= –1,4

Дифференцируя по x левую и правую части уравнения (8.3)

y'''= – 0,2y'y'' – 0,1(xy'+y) – y',

y⁽⁴⁾= – 0,2(y'y'''+y''²) – 0,1(xy''+2y') – y'',

y⁽⁵⁾= – 0,2(y'y⁽⁴⁾+3y''y''') – 0,1(xy'''+3y'') – y''',

y⁽⁶⁾= – 0,2(y'y⁽⁵⁾+4y''y⁽⁴⁾+3y'''²) – 0,1(xy⁽⁴⁾+4y''' – y⁽⁴⁾)

Подставляя начальные условия и значение y''(0), находим y'''(0)= – 1,54;

y⁽⁴⁾(0)= – 1,224; y⁽⁵⁾ (0)=0,1768; y⁽⁶⁾(0)= – 0,7308. Таким образом, искомое приближенное решение запишется в виде: y(x) ≈ 1 + 2x – 0,7x² – 0,2567x³ + 0,051x⁴ + 0,00147x⁵ – 0,00101x⁶.

8.2 Метод эйлера

Простейшими из численных методов решения дифференциальных уравнений является метод Эйлера, который основан на замене искомой функции многочленом первой степени, т.е. линейной экстраполяцией. Речь идет о нахождении значений функции в соседних точках аргумента x не между ними.

Выберем шаг h малым, чтобы для всех x между x₀ и x₁=x₀+h значение функции y мало отличалось от линейной функции. Тогда на указанном интервале y = y₀ + (x – x₀)y' = y₀ + (x –

– x0)f'(x0y0), где y'0 = f'(x0,y0) – значение производной в точке х=х0 (см. Рисунок) Таким образом, кривая на этом участке заменяется отрезком прямой (касательной к кривой в начале участка). Для точки x1=x0+h, y1=y0+hy'0. Для точки x2=x1+h, y2=y1+hy'0.

Продолжая таким же способом определять значения функции, убеждаемся, что метод Эйлера представляется в виде последовательного выполнения формул:

∆

(8.4)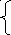

y_k = y'_kh

y_k+1 = y_k + ∆y_k

ПРИМЕР

Решим методом Эйлера уравнения y' = x – y с начальным условием х₀=0, у₀=0 на отрезке [0,1] с шагом h=0,1.

Вычисления приведены в таблице.

Первая строка в столбцах 1 и 2 заполнена по начальным данным. Затем вычисляется у' по заданному уравнению (в столбце 4), затем ∆y = y'h – в столбце (4).

Столбец (5) содержит таблицу значений точного решения заданного уравнения.

х у ∆y у уточн 0 0 0 0 0 0.1 0 0.01 0.10 0.00 0.2 0.01 0.02 0.19 0.02 0.3 0.03 0.03 0.27 0.04 0.4 0.06 0.03 0.34 0.07 0.5 0.09 0.04 0.41 0.11 0.6 0.13 0.05 0.47 0.15 0.7 0.18 0.05 0.52 0.20 0.8 0.23 0.06 0.57 0.25 0.9 0.29 0.06 0.61 0.31 1 0.35 0.37

Из таблицы видно что при х=1 относительная ошибка метода Эйлера составляет δ=0,37 — 0,35/0,37*100%≈5,4%

УТОЧНЕННЫЙ МЕТОД ЭЙЛЕРА

При том же объеме вычислительной работы дает более высокую точность.

Ранее мы считали подынтегральную функцию постоянной, равной её значению f(x_k,y_k) на левом конце участка. Более точное значение получится если полагать f(x,y(x)) равной значению в центре участка. Для этого надо брать двойной участок (x_k-1,x_k+1), заменив формулу

y_k+1=y_k+∆y_k на y_k+1=y_k-1+2hy'_k (8.5)

Эта формула и выражает уточненный метод Эйлера. Но в этом случае надо придерживать следующей последовательности действий:

х у ∆y у' уточн 0 0 0 0 0 0.05 0 0.005 0.050 0.001 0.1 0.005 0.10 0.095 0.005 х у ∆y у' уточн 0.2 0.019 0.036 0.181 0.019 0.3 0.041 0.052 0.259 0.041 0.4 0.071 0.066 0.329 0.070 0.5 0.107 0.079 0.393 0.107 0.6 0.150 0.090 0.450 0.149 0.7 0.197 0.101 0.503 0.197 0.8 0.251 0.110 0.549 0.249 0.9 0.307 0.119 0.543 0.307 1.0 0.37 0.368

y1/2=y0+h/2y' y1=y0+hy' y2=y0+2hy' Далее расчёты вести по формуле (8.5). ПРИМЕР Для сравнения рассмотрим то же уравнение y' = x – y с начальными условиями x0=0, y0=0. Уточненный метод, как видно из таблицы дает более высокую точность относительная погрешность при х=1, у=0,370, а уточн 0,368.