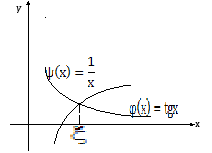7.2 Погрешность приближнного значения

КОРНЯ.

Если ξ-точное значение корня уравнения , -его приближенное значение на отрезке [a,b], причем (-наименьшее значение функции в данном интервале), то погрешность приближенного значения корня будет:

Пример: Приближенным корнем уравнения является . Оценить абсолютную погрешность этого корня.

Решение: Имеем , то точный корень ξ содержится в интервале (1,22;1,23). Производная монотонно возрастает, поэтому её наименьшем значением в данном интервале является:

Отсюда .

7.3 Графическое решение уравнений.

В отдельных случаях приближенное решение уравнения можно найти графическим методом. Пусть требуется найти корни уравнения . Заменим это уравнение равносильным:

;

где - более простые функции. Построим графики этих функций, получим корни уравнения , как координаты x точек пересечения ;

ПРИМЕР: Решить уравнение .

Заменим его равносильным уравнением: , где . Построив их графики, найдем точку пересечения , которая и является решением исходного уравнения.

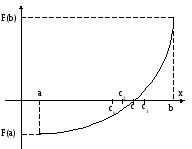
7.4 Метод половинного деления

(МЕТОД БИССЕКЦИИ).

Пусть требуется найти корень уравнения на отрезке [a,b]. Отрезок [a,b] либо задан заранее, либо получен методом отделения корней. Метод деления отрезка пополам проиллюстрирован на рисунке.

Пусть , в качестве начального приближения корня примем . Поскольку , то рассматриваем отрезок []. Следующее приближение , при этом отрезок [] отбрасывается таким образом. Аналогично находим другие приближения , и т.д. до выполнения условия .

Итерационный процесс можно завершить тогда, когда значение функции после к-ой итерации станет меньшим по модулю заданной , т.е. .

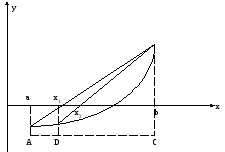
7.5 Метод хорд

(ПРОПОРЦИОНАЛЬНЫХ ЧАСТЕЙ).

Отрезок [a,b] либо задан заранее, либо получен методом отделения корней. Пусть . Соединим хордой точки A и B, из подобия ∆ABC и ∆Ax1D: , x1 = a – .

Это будет первым приближением к корню уравнения . Сравнивая знаки , видим, что корень находится на отрезке [x,b]. Следующее приближение к корню x₂ получаем в точке пересечения с осью x ходы, соединяющей . Её координаты определяются аналогично, x₁ по формуле:

Последующие итерации выполняются по формуле:

Итерации продолжаются до тех пор, пока значение не станет меньше наперед заданного числа (погрешность расчета) .

Если , то формула для расчета корня имеет вид , погрешность приближенного решения можно оценить по формулам , где ; , где - точное значение корня.

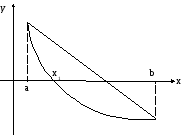
7.6 Метод ньютона

(МЕТОД КАСАТЕЛЬНЫХ).

Его отличие от предыдущего метода состоит в том, что вместо хорды проводится касательная кривой y=f(x) в точке c₀. При этом не обязательно задавать отрезок [a,b], содержащий корень, а достаточно лишь найти начальное приближение корня. В точке c₀ проводим касательную к кривой f(x). Точка пересечения её с осью дает первое приближение

корня. Затем проводим перпендикуляр к оси x в точке x1 и получаем точку c1. Далее снова проводим касательную к f(x) в точке c1. Ее пересечение с осью x дает следующее приближение x2 и т.д., пока не будет выполнено условие , где -погрешность расчета.

Расчетную формулу можно получить из геометрических соображений из треугольника x₁bc₀ имеем:

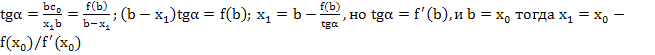а для последующих точек .

Оценка погрешности решения производится по формулам:

²

Здесь m₁=min f’(x), а M₁=max f’(x) на отрезке [a,b]. Это самый эффективный, быстро сходящийся метод.