2) Метод трапеций.

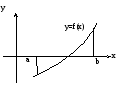
В этом методе также разбивают отрезок [a,b] на n равных частей с шагом Затем точки ординат y0, y1,…, yn соединяют хордами. В результате непрерывная кривая f(x) заменяется

ломанной линией и определённый интеграл заменяется суммой площадей трапеций. Площадь отдельной трапеции:

Определённый интеграл будет равен:

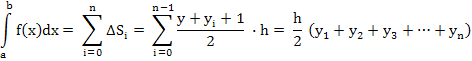
3) Метод симпсона.

Более точным, нежели рассмотренные ранее, является метод Симпсона.

Разобьём участок [a,b] на чётное число участков. Рассмотрим пару соседних участков x0x1 и x1x2. Проведём через 3 точки кривой f(x) параболу, управление которой y = Ax2 + Bx + C. Заменив площадь заданной криволинейной трапеции на участке [x0,x2] площадью ограниченной трапеции к

приближённому равенству:

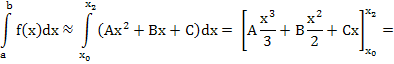
Вынося за скобки (x₂ – x₀) и приводя к общему знаменателю, получим:

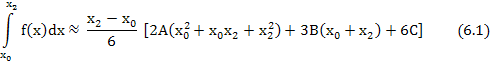
Неизвестные A,B,C находятся из условия, что при значениях x, равных x₀, x₁, x_2, функция f(x) принимает значения y₀, y₁, y₂. Заметим, что x1 = , запишем эти условия в виде:

(6.2)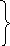

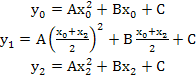
Умножая второе равенство на четыре и складывая все три равенства (6.2), находим:

y₀ + 4y₁ + y₂ = A + B + 6C = 2A + 3B(x₀+x₂) + 6C, (6.3)

а это совпадает с квадратной скобкой формулы (6.1).

Подставив (6.3) в (6.1) и заметив, что х₂ – х₀ = 2h, получим

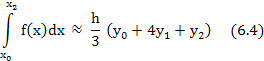
Ясно, что для каждой следующей пары участков получится такая же формула.

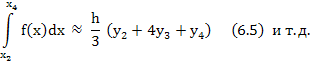
Суммируя равенство вида (6.4) и (6.5) по всем участкам и определенным образом сгруппировав элементы, получим:

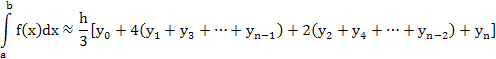
Полученное соотношение называется формулой Симпсона или формулой парабол. В ней все ординаты с нечетными номерами умножаются на четыре, а все ординаты с четными номерами (кроме крайних) – на два.

7. Приближенное решение

НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Корнем (решением) нелинейного уравнения f(x) называется такое x=ξ, при котором f(ξ)=0.

Нелинейные уравнения бывают алгебраические и трансцендентные. Алгебраические уравнения – это уравнения, содержащие алгебраические функции.

Уравнения, содержащие тригонометрические, показательные, логарифмические функции называются трансцендентными.

Методы решения нелинейных уравнений бывают прямыми и итерационными, т.е. методы последовательных приближений.

Приближенное нахождение изолированных корней обычно состоит из двух этапов:

1) отделение корней, т.е. определение промежутков [a,b], содержащих отдельные корни;

2) уточнение приближенных корней, т.е. доведение до заданной точности.

7.1 Использование конечных разностей для

ДИФФЕРЕНЦИРОВАНИЯ.

При отделении корней пользуются теоремой:

Если непрерывная функция f(x) принимает значение разных знаков на концах отрезка [a,b], то внутри этого отрезка содержится, по меньшей мере, один корень уравнения f(x)=0. Корень будет единственным, если первая производная f’(x) существует и сохраняет

постоянный знак на интервале [a,b]. Отделение корней начинаем с определения знаков f(x). Чтобы убедиться в существовании единственного корня на отрезке, нужно провести процесс половинного деления, определяя знаки f(x) в точках деления.

Пример: Определить корни уравнения f(x)=x3 – 6x + 2 = 0.

x f(x) x f(x) –∞ –3 –1 0 – – + + 1 3 +∞ – + +

Это уравнение имеет 3 действительных корня. Из таблицы знаков функции видно, что функция имеет три корня в интервалах (–3, –1), (0,1), (1,3).