Алгебраическая система

Алгебраическая система

Алгебраической системой A называется совокупность ‹M,O,R›, первая составляющая которой M есть непустое множество, вторая компонента O – множество алгебраической операций, третья компонента R – множество отношений на множестве M.

Пояснение.

1. Множество M алгебраической системы A называют несущим, или основным множеством.

2. Совокупность алгебраических операций и отношений алгебраической системы называют сигнатурой Σ. В этом случае алгебраическая система записывается парой ‹M, Σ.› .

3. Алгебраическая система ‹M,O› называется универсальной алгеброй (или просто алгеброй), если на основном множестве M множество отношений R пусто (т.е. R = ).

4. Алгебраическая система A = ‹M,R› называется реляционной системой (или моделью), если на основном множестве M заданы только отношения R (т.е. в этом случае пусто множество операций O, что означает O = ).

Пример 1. Алгебраической системой является аксиоматическая теория множеств ‹M, , -, › (где O = {, -} – множество из операций объединения и операций дополнения -, аR = {} – множество, состоящее из отношения включения .

Пример 2. Алгебра Кантора (алгебра множеств) - ‹B(M), , ›, несущим множеством является булеан B(A) (т.е. множество всех подмножеств данного множества U), а множеством операций O = {, , -} -, булевы операции объединения , пересеченияи дополнения -.

Пример 3. Метрическое пространство ‹M,R›, где R – метрика, является реляционной системой. Пояснение. Пространство – множество объектов (точек) с введенным отношением между точками и операциями над элементами множества. Метрическое пространство – это множество точек Х с расстоянием между ними d≥0, удовлетворяющее трем аксиомам:

1. Аксиома идентичности. d=0 тогда и только тогда , когда x=y.

2. Аксиома симметрии. d(х,y)=d(y,x).

3. Аксиома треугольника. d(х,y)=d(y,z)+d(z,y), где

Расстояние d(х,y) называется метрикой, а пара ‹X,d› - метрическим пространством.

Замыкание и подалгебры

Подмножество называется замкнутым относительно операцииφ, если

Если X замкнуто относительно всех , тоназываетсяподалгеброй алгебры , где,k = n_i/

Пример 1. Алгебра - поле действительных чисел.

Тип – (2,2).

Все конечные подмножества, кроме {0}, не замкнуты относительно сложения и все конечные подмножества, кроме {0} и {0,1}, не замкнуты относительно умножение.

Кольцо целых чисел образует подалгебру рациональных и, соответственно, вещественных чисел.

Пример 2. Алгебра -алгебра подмножеств над множеством M.

Тип – (2,2,1).

При этом - подалгебра.

Пример 3. Алгебра гладких функций , где- операция дифференцирования.

Множество полиномов одной переменной x образует подалгебру которая обозначается R[x].

Тип – (1).

Теорема. Непустое пересечение подалгебр образует подалгебру.

Доказательство. Пусть - подалгебра алгебры. Тогда

Замыканием множества относительно сигнатурыΣ (обозначается [X]_Σ) называется множество всех элементов (включая сами элементы X), которые можно получить из X, применяя операции из Σ.

Морфизмы

Из вышеприведенных определений следует, что каждая алгебраическая структура выделяет класс отображений между объектами с данной структурой, согласованных с операциями этой структуры.

Такие отображения называются морфизмами. Изоморфизм множеств был рассмотрен выше.

Гомоморфизмы

Алгебры с различными типами имеют различное строение. Пусть A = иB = - две алгебры одинакового типа. Если существуетf: A → B, такая что

,

то говорят, что f - гомоморфизм из A в B (гомоморфизм «уважает» операции)

Пусть A = ,B = , тип = (1) иf: A → B. Действие этих функций изобразим с помощью следующей диаграммы:

φ

A → A

f↓ ↓f

B → B

Пусть f – гомоморфизм. Если взять конкретное и двигаться по двум различным путям на диаграмме, то получится один и тот же элемент(так какf(φ(a)) = ψ(f(a))), т.е. диаграмма коммутативна. Коммутативной диаграмма называется потому, что условие гомоморфизма можно переписать так

где - суперпозиция функций.

Рассмотрим морфизмы с другой стороны.

Пусть даны алгебраические системы A = ,B = . Отображениеφ: A → B называется гомоморфизмом системы A в систему B, если выполняются следующие условия:

1) для любого функционального символа f⁽ⁿ⁾,соответствующих функций f_А и f_В в системах A и B и любых a₁, a₂, …, выполняется

2) для любого предикатного символа соответствующих предикатовP_А и P_В в системах A и B и любых a₁, a₂, …,a_n выполняется

Если φ: A → B – гомоморфизм , то будем его обозначать φ: A → B

При гомоморфизме сохраняются действий операций и отношения. Это позволяет переносить изучение свойств с одной системы на другую.

Пример. Пусть A = ,B = , гдеN₁₀ +{0,1,2,3,4,5,6,7,8,9}, а +₁₀ - сложение по модулю 10. Тогда f:=a mod 10 - гомоморфизм из A в B.

Гомоморфизм, обладающий дополнительными свойствами, имеют специальные названия.

Гомоморфизм, который является инъекцией, называется мономорфизмом.

Гомоморфизм, который является сюръекцией, называется эпиморфизмом.

Гомоморфизм, который является биекцией, называется изоморфизмом.

Если A = B, то гомоморфизм называется эндоморфизмом, а изоморфизм называется автоморфизмом.

Фундаментальные алгебры

На множестве М может быть задано много различных операций. Чтобы выделить одну из них используют обычно скобки <М, *> и говорят, что операция * определяет на М алгебраическую структуру. Так, например, на множестве целых чисел помимо хорошо известных операций сложения и умножения целых чисел n и m можно ввести много других, например, операцию ○ суть которой состоит в следующем m○n = n m - 3n и т.п.

В зависимости от операции получаем различные алгебраические структуры: <М, *>; <М, +>; <М, х>; <М, ○>. Это бинарные операции, но операции могут быть в общем случае n–арными: при n = 1 – унарные, при n = 2 – бинарные, при n = 3 – тернарные и т.д. и их комбинации. Такие алгебраические структуры составляют специальную теорию универсальных алгебр. Изучение в общем виде алгебр для нас не представляет практического интереса, поэтому рассмотрим наиболее часто используемые алгебры, т.е. фундаментальные алгебры.

Подведем итог сказанному. Алгебра A = – это совокупность A носителя и сигнатуры Σ. Носитель A – это множество, которое может состоять из нескольких множеств, тогда алгебра будет называться многоосновной. Сигнатура Σ также является множеством, элементами которого являются множества {F_1,i1 , F_2,i2 , …,F_n,in,}, где первый индекс указывает местность операции, а второй индекс указывает порядковый номер, например, операции F_2,i2 – бинарные операции, номер данной операции i₂, где i₂ принимает значения 1, 2, …, n₂.

Алгебры с унарными операциями

Самые простые алгебры A = – это алгебры с унарными операциями F_1,i1, где i₁ принимает значения 1, 2, …, n₁. Эти операции определяют свойства элементов и самой простой алгеброй будет алгебра, когда i₁ = 1, т.е. A = .

Алгебры с бинарными операциями

Бинарные алгебры имеют вид A = – это алгебры с бинарными операциями F_2,i2, где i₂ принимает значения 1, 2, …, n₂. Из этих алгебр самой простой будут алгебры с одной бинарной операцией, т.е. A = , где A = MM, а F_2,1 =*, т.е. *: MM → M. Рассмотрим более подробно эти алгебры.

Алгебры с одной бинарной операцией

Пусть на множестве М задана одна бинарная операция. Рассмотрим порождаемые ею алгебры, но предварительно рассмотрим некоторые свойства бинарных операций.

Бинарная операция * на множестве М называется ассоциативной, если a*(b*c) = (a*b)*c для всех a, b, c принадлежащих множеству М.

Бинарная операция * на множестве М называется коммутативной, если a*b = b*a для всех a, b принадлежащих множеству М. Требования коммутативности и ассоциативности независимы, т. из ассоциативности не следует коммутативность и наоборот.

Пример.

1. На множестве целых чисел n и m задана алгебраическая структура <М, *> такая, что n*m = -m – n = . Эта алгебраическая структура коммутативна, что очевидно n*m = -n – m = -m – n = m* n, но не ассоциативна:

m*(n*p) = -m - (n*p) = -m - (-n - p) = -m + n + p;

(m*n)*p = -(m*n) – p = -(- m - n) – p = m + n – p

Таким образом m*(n*p) ≠ (m*n)*p, т.е. эта алгебраическая структура не ассоциативна.

2. Рассмотрим множество М_n(R) всех квадратных матриц порядка n>1 на котором задана операция умножения Ч в обычном смысле. Так построенная алгебраическая структура ассоциативна, но не коммутативна. (докажите)

Названия свойств операций будут присваиваться и соответствующим алгебраическим структурам <М, *>, т.е. коммутативная или ассоциативная алгебраическая система или то и другое одновременно.

Рассмотрим еще один элемент e множества М, который может быть только один, если он существует на данной алгебраической структуре. Этот элемент e называется нейтральным или единичным. Он обладает свойствами: во-первых, e М, а во-вторых, для любого элемента m М выполняется равенство – 'e*М = М*e' = М, где 'e, e' - соответственно левый и правый нейтральный элемент.

Полугруппа

Множество М с заданной на нем бинарной ассоциативной операцией f₂ называется полугруппой <М, f₂>. Пусть S полугруппа на алгебраической структуре с f₂ ≡ *. Подмножество S' S называется подполугруппой, если а*b S' для всех а, b S', тогда подмножество S' замкнуто относительно операции *. Для полугруппы для любых a, b, c принадлежащих М выполняется для бинарной операции условие

a * (b * c) = (a * b) * c

Пример 1. Множество непустых слов A⁺ в алфавите A образует полугруппу относительно бинарной операции конкатенации.

Пример 2. Любое множество функций, замкнутое относительно суперпозиции, образует полугруппу.

Если в полугруппе существует система образующих, состоящая из одного элемента, то такая полугруппа называется циклической.

Пример 1. <N, +> является циклической полугруппой, поскольку {1} является системой образующих, т.е каждое натуральное число можно представить, как последовательность знаков 1. Различные слова в алфавите {1} это различные элементы носителя, то есть эта полугруппа свободна.

Теорема (Маркова-Поста). Существует полугруппа, в которой проблема распознования равенства слов алгоритмически неразрешима.

Моноид

Полугруппа с единичным (нейтральным элементом) принято называть моноидом или просто полугруппой с единицей. Мощность моноида, как множества обозначается |М| или Card М.

Моноид – это полугруппа с единицей.

Теорема. Единица моноида единственна.

Доказательство. Пусть . Тогда

Теорема. Всякий моноид над М изоморфен некоторому моноиду преобразований над М.

Доказательство. Пусть М = <М, *> - моноид над М = {e,a,b,c, ….}. Построим . Тогда

Группоид

Алгебра вида <М, f₂> называется группоидом.

Если f₂ — операция типа умножения (), то группоид называютмультипликативным, если f₂ - операция типа сложения (+), то аддитивным.

Пусть А = <М, f₂) — группоид; обозначим операцию f₂ как . Тогда элементназываетсяправым нейтральным элементом группоида А, если для всякого выполняется равенствоте = т ; элемент группоидаА = <М,> называется левым нейтральным элементом, если для всех выполняется равенствоет = т. В этих определениях использовались выражения «все элементы», «всякий элемент». В дальнейшем для краткости вместо слов «все» или «всякий» будем использовать символ (перевернутая букваА — первая буква английского слова All — все). Если элемент е, , группоида А = <М, > является одновременно левым и правым нейтральным элементом, то его называют двусторонним нейтральным элементом или просто нейтральным элементом.

Никакой группоид не может иметь более одного нейтрального элемента. Действительно, если

те = ет = т и те'=е'т=т

справедливо для всех , то

е' = е'е = е.

Если группоид <М,> мультипликативный, то нейтральный элемент называется единицей и обозначается 1; если аддитивный, то нейтральный элемент называется нулем и обозначается 0.

Группоид А = <М,> называется идемпотентным, если его сигнатура удовлетворяет закону идемпотентности

.

Группоид <М,>, сигнатура которого удовлетворяет закону коммутативности

.

называется коммутативным или абелевым.

Группоид <М,>, в котором выполняется закон ассоциативности называетсяассоциативным или полугруппой.

Группа

Полугруппа <М,> в которой выполнимы обратные операции: для любых каждое из уравнений, обладает единственным решением, называетсягруппой.

Пример.

Рассмотрим понятие группы на примере группы подстановок, содержащей шесть элементов. Группу подстановок исследовал выдающийся французский математик Галуа в связи с решением уравнений в радикалах.

Подстановкой n-й степени называется взаимно однозначное отображение множества из п элементов на себя.

Рассмотрим три элемента: х₁, х₂, х₃. Существует шесть перестановок из трех элементов (3! = 6): х₁х₂х₃, х₂х₃х₁, х₁х₂х₃, х₃х₁х₂, х₂х₁х₃, х₃х₂х₁. Запишем две перестановки из трех элементов друг под другом:

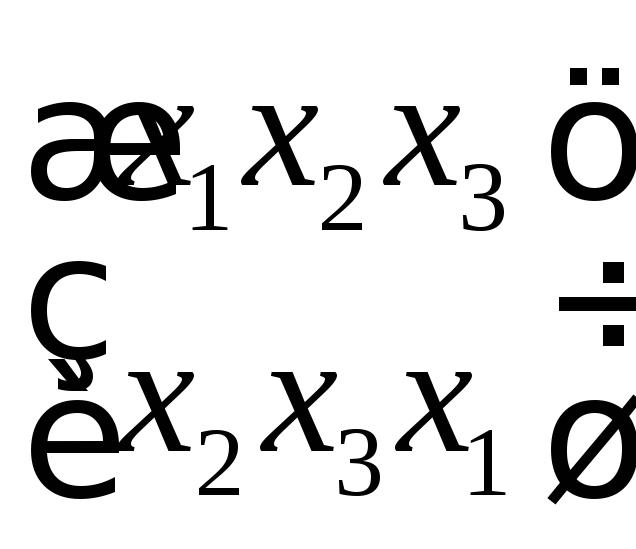
Эта запись означает, что х₁ переходит в х₂, х₂ - в х₃, х₃ – в х₁.

Число возможных подстановок равно числу перестановок. Введем следующие обозначения для шести возможных подстановок:

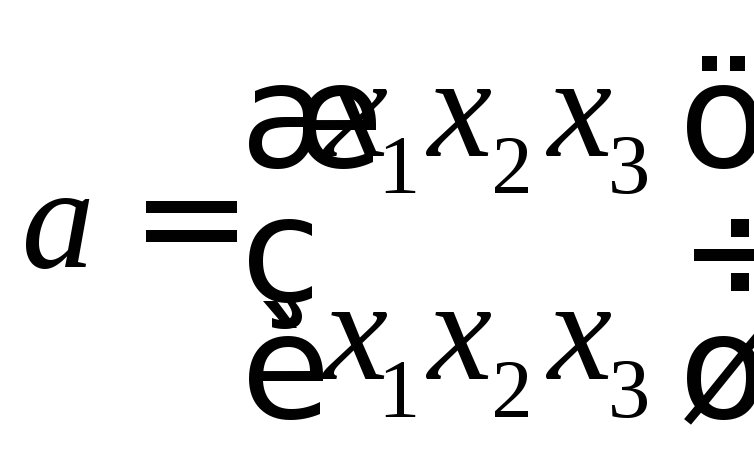
Введем операцию умножения над подстановками.

Произведением подстановок называется подстановка, получаемая в результате последовательного выполнения сначала первой, а затем второй из перемноженных подстановок. Например,

Выражение бв, б,в = а, b, с, d, е, f определяет табл. 1.1.

Таблица 1.1

б	в
	а	b	с	d	е	f
a	а	b	с	d	е	f
b	b	а	d	с	f	е
c	с	е	а	f	b	d
d	d	f	b	е	а	с
е	е	с	f	а	d	b
f	f	d	е	b	с	а

В рассматриваемой алгебре <М, > выполняется закон ассоциативности, но не выполняется закон коммутативности.

Абелева группа

Группа с коммутативной операцией называется коммутативной, но чаще ее называют абелевой в честь норвежского математика Абеля. Термин «группа» ввел французский математик Галуа, который и является создателем теории групп.

Алгебра с двумя операциями

Рассмотрим алгебраические структуры с двумя операциями. Эти структуры нашли широкое применение при решении практических задач.

Кольца

Алгебра <М, , +>, которая по умножению является мультипликативным группоидом, по сложению — абелевой группой, причем умножение связано со сложением законами дистрибутивности

а(b + с) = аb + aс,

(b + с) а =bа + са,

называется кольцом.

Тело

Кольцо, в котором все отличные от нуля элементы составляют группу по умножению, называется телом.

Поля

Тело, у которого мультипликативная группа абелева, называется полем.

Отношения

Фундаментальным понятием дискретной математики является понятие отношения, которое используют для обозначения связи между объектами или понятиями.

Квадратом множества М называется декартово произведение двух равных между собой множеств: ММ = М². Бинарным отношением Т в множестве М называется подмножество его квадрата: . Элементы т_i, и т_j, находятся в отношении T, если .

Граф

Совокупность множества М с заданным в нем бинарным отношением называетсяграфом G:

,

где М - носитель графа (множество вершин); Т - сигнатура графа (множество дуг).

Рассмотрим задание бинарного отношения с помощью матрицы смежности и фактор-множества.

Матрица смежности

При матричном задании используют двумерную таблицу — матрицу смежности, каждой строке (столбцу) которой взаимно однозначно сопоставляют элемент множества М. Тогда каждая клетка (i, j) взаимно однозначно соответствует элементам множества М². Клетку (i, j), которая соответствует элементу, принадлежащему , как-то отличают, например зачерняют или помещают в нее единицу; остальные клетки оставляют незачерненными или записывают в них нули.

Пример.

Рассмотрим предложенную фон Нейманом блок-схему ЭВМ, которая состоит из множества устройств

Фактор-множества и фактор-алгебра

Если отношение R обладает свойствами: рефлексивное симметричное транзитивное, т.е. является отношением эквивалентности (~ или ≡ или Е) на множестве M, то множество классов эквивалентности называется фактор множеством множества M относительно эквивалентности R и обозначается M/R

Здесь есть подмножество элементов множестваM эквивалентных x , называемых классом эквивалентности.

Из определения фактор-множества следует, что оно является подмножеством булеана: .

Функция называетсяотождествлением и определяется следующим образом:

Теорема. Фактор-алгебра F_n/~ изоморфна алгебре булевых функций B_n

Доказательство.

Искомый изоморфизм ξ: F_n/~ → B_n определяется по следующему правилу: классу эквивалентности ~(φ) сопоставляется функция f_φ, имеющая таблицу истинности произвольной формулы из множества ~(φ). Поскольку разным классам эквивалентности соответствуют различные таблицы истинности, отображение ξ инъективно, а так как для любой булевой функции f из В_п найдется формула , представляющая функциюf, то отображение ξ сюръективно. Сохранение операций , 0, 1 при отображении ξ проверяется непосредственно. ЧТД.

По теореме о функциональной полноте каждой функции , не являющейся константой0, соответствует некоторая СДНФ ψ, принадлежащая классу ~(φ) = ξ^-1(f) формул, представляющих функцию f. Возникает задача нахождения в классе ~(φ) дизъюнктивной нормальной формы, имеющей наиболее простое строение.

Целые числа по модулю m

Дано кольцо целых чисел <Z; +, >.

Напомним. Алгебра <М, , +>, которая по умножению является мультипликативным группоидом, по сложению — абелевой группой, причем умножение справа и слева связано со сложением законами дистрибутивности называется кольцом.

Возьмем целое число m>1. Зададим отношение эквивалентности на множестве целых чиселZ по следующему правилу:

ba b - a = m q для некоторого .

Напомним. Пусть Е – эквивалентность на множестве A. Классом эквивалентности элемента называетсямножество .

Класс эквивалентности элемента a по модулю m – это множество = {…, -3m+a, -2m+a, -m+a, a, m+a, 2m+a, 3m+a, …}, которое обозначается через a+Zm или просто .

Пример. Если m=5, то при соответственно a=0, 1, 2, 3, 4 классы эквивалентности элементов a по модулю 5 будут соответственно равны

; ;

; .

Таким образом, множество Z разбивается на непересекающиеся подмножества ,,,,, т.е.Z = и попарные пересеченияи т.д.

Напомним. Множество называетсяфактор-множеством множество A по отношению E.

Фактор-множеством целых чисел Z по отношению целые числа по модулю 5 является множество . Мощность этого множества равна 5.

В общем случае множество содержитm элементов.

Вместо записи пишутb ≡ a (mod m) читается «b равно a по модулю m» или «b сравнимо с a по модулю m».

Множество обозначается также черезZ_m и называется множеством вычетов или множеством целых чисел по модулю m.

Конгруэнции

Конгруэнцией на алгебре A = <A; Σ> (Σ – сигнатура алгебры состоит только из функциональных символов) называется такое отношение эквивалентности , при котором для любого, любогоn-местного символа произвольных наборов(a₁, a₂, … ,a_n), (b₁, b₂, … ,b_n) Aⁿ, если a₁θb₁, a₂θb₂, …, a_nθb_n, то f(a₁, a₂, … ,a_n)θf(b₁, b₂, … ,b_n), т.е. все операции согласованы с отношением эквивалентности θ.

Пример. Для двухместной операции сложения это выглядит так: для любых x и y из A и любых ,элементa+b принадлежит классу θ(x+y).

Лемма. Отношение является конгруэнцией на алгебре<Z; +, >.

Наибольший общий делитель чисел a и b обозначается (a, b)или НОД(a, b). Два целых числа a и b называются взаимно простыми если (a, b) = 1.

Теорема. Тогда и только тогда элемент a кольца Z_m имеет обратный (т.е. элемент a^-1 такой, что a a^-1 = 1), когда (a,m) = 1.

Теорема. Кольцо вычетов <Z_m; +, > тогда и только тогда является полем, когда m простое число.

Замечание

1. Для построения логической теории используются формализованные языки (непустое множества алфавита, синтаксиса и семантики), которые являются средством познания мира и средством выражения мысли.

δ = ‹ A, S₁, S₂› (A- символы алфавита, S₁- синтаксис, S₂- семантика).

2. В рамках формализированных языков строятся логические теории, с помощью которых решаются логические задачи.

3. Во множестве формул языка выделяют класс формул - аксиомы (логич. закон, базис) Например, выражение xне x = 1

4. Выделяют множество переходов, т.е. с помощью переходов от одной формулы к другой находят правильные умозаключения.

Контрольные вопросы

Лекция № 7

Для математиков XIXв., занимавшихся алгеброй логики, наиболее важной проблемой было развитие технических приемов оперирования с элементарными утверждениями булевой алгебры, подобных тем, которые имеются в элементарной алгебре.

Х. Карри. Основания математической логики. М.: Мир,- 1969, стр. 420