
- •§1. Определение производной.
- •§ 2. Производные от некоторых
- •§3. Основные правила дифференцирования.
- •§4. Производная сложной функции.
- •§ 5. Дифференцирование обратной функции.
- •§6.Производная логарифмической функции.
- •§8. Производные обратных тригонометрических функций.
- •§9. Производная показательной функции.
- •§10.Таблица основных формул дифференцирования.
- •§11. Производные высших порядков.
- •§ 12. Экстремум функции. Возрастание и убывание функции.
- •§13. Касательная и нормаль к линии.
Производная функции одной переменной.
Введение.
Настоящие методические разработки предназначены для студентов факультета промышленное и гражданское строительство. Они составлены применительно к программе курса математики по разделу «Дифференциальное исчисление функций одного переменного».
Разработки представляют собой единое методическое руководство, включающее в себя: краткие теоретические сведения; «типовые» задачи и упражнения с подробными решениями и пояснениями к этим решениям; варианты контрольной работы.
В конце каждого параграфа дополнительные упражнения. Такая структура разработок делает их пригодными для самостоятельного овладения разделом при самой минимальной помощи со стороны преподавателя.
§1. Определение производной.
Механический и геометрический смысл
производной.
Понятие производной является одним из самых важных понятий математического анализа.Оно возникло еще в 17 веке. Формирование понятия производной исторически связано с двумя задачами: задачей о скорости переменного движения и задачей о касательной к кривой.
Эти задачи, несмотря на их различное содержание, приводят к одной и той же математической операции, которую нужно провести над функцией.Эта операция получила в математике специальное название. Она называется операцией дифференцирования функции. Результат операции дифференцирования называется производной.
Итак, производной функцииy=f(x)
в точкеx0 называется
предел (если он существует) отношения
приращения функции
![]() к приращению аргумента
к приращению аргумента
![]() при
при
![]() .
.
Производную принято обозначать
так:
![]() .
.
Таким образом, по определению
![]() .
.
Для обозначения производной употребляются
также символы
![]() .
.
Механический смысл производной.
Если s=s(t)
– закон прямолинейного движения
материальной точки, то
![]() есть скорость этой точки в момент времениt.
есть скорость этой точки в момент времениt.
Геометрический смысл производной.
Если функция y=f(x)
имеет производную в точке![]() ,
то угловой коэффициент касательной к
графику функции в точке
,
то угловой коэффициент касательной к
графику функции в точке![]() равен
равен
![]() .
.
Пример.
Найдите производную функции
![]() в точке
в точке![]() =2:
=2:
1) Дадим точке
![]() =2
приращение
=2
приращение![]() .
Заметим, что
.
Заметим, что![]() .
.
2) Найдем приращение функции в точке
![]() =2:
=2:
![]()
3) Составим отношение приращения функции к приращению аргумента:
![]() .
.
Найдем предел отношения при
![]() :
:
![]() .
.
Таким образом,
![]() .
.
§ 2. Производные от некоторых
простейших функций.
Студенту необходимо научиться вычислять
производные конкретных функций: y=x,y=![]() и вообщеy=
и вообщеy=![]() .
.
Найдем производную функции у=х.
Имеем:
 т.е.
(x)′=1.
т.е.
(x)′=1.
Найдем производную функции
![]()
![]()
Производная
![]()
Пусть
![]() тогда
тогда

Легко заметить закономерность в
выражениях производных от степенной
функции
![]() приn=1,2,3.
приn=1,2,3.
Следовательно,
![]() . (1)
. (1)
Эта формула справедлива для любых действительных n.
В частности, используя формулу (1), имеем:
![]() ;
;
![]() .
.
Пример.
Найдите производную функции
![]() .
.
Решение:
 .
.
Данная функция является частным случаем функции вида
![]() при
при
![]() .
.
Используя формулу (1), имеем
 .
.
Производные функций y=sin x и y=cos x.
Пусть y=sinx.
![]()
Разделим на ∆x, получим

Переходя к пределу при ∆x→0, имеем

Пусть y=cosx .
Тогда
![]()
Отсюда

Переходя к пределу при ∆x→0, получим

![]() ;
;![]() .
(2)
.
(2)
§3. Основные правила дифференцирования.
Рассмотрим правила дифференцирования.
Теорема 1. Если функцииu=u(x) иv=v(x) дифференцируемы в данной точкеx,то в этой точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых: (u+v)'=u'+v'.(3)
Доказательство: рассмотрим функцию y=f(x)=u(x)+v(x).
Приращению ∆x аргумента x соответствуют приращения ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) функций u и v. Тогда функция y получит приращение
∆y=f(x+∆x)-f(x)=
=[u(x+∆x)+v(x+∆x)]--[u(x)+v(x)]=∆u+∆v.
Следовательно,
![]()
Итак, (u+v)'=u'+v'.
Теорема 2.Если функцииu=u(x) иv=v(x) дифференцируемы в данной точкеx, то в той же точке дифференцируемо и их произведение.При этом производная произведения находится по следующей формуле: (uv)'=u'v+uv'. (4)
Доказательство: Пусть y=uv, где u и v – некоторые дифференцируемые функции от x. Дадим x приращение ∆x;тогда u получит приращение ∆u, v получит приращение ∆v и y получит приращение ∆y.
Имеем y+∆y=(u+∆u)(v+∆v), или
y+∆y=uv+u∆v+v∆u+∆u∆v.
Следовательно, ∆y=u∆v+v∆u+∆u∆v.
Отсюда
![]()
Переходя к пределу при ∆x→0 и учитывая, чтоuиvне зависят от ∆x, будем иметь
![]()
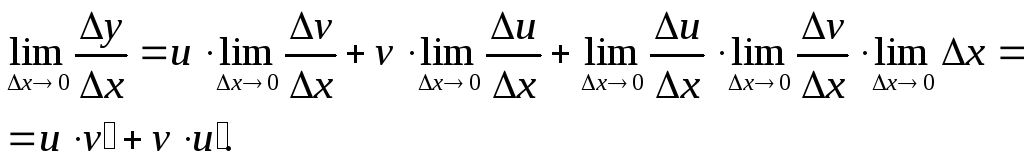
Теорема 3. Производная частного двух функций равна дроби, знаменатель которой равен квадрату делителя, а числитель- разности между произведением производной делимого на делитель и произведением делимого на производную делителя, т.е.
Если
![]() то
то![]() (5)
(5)
Теорема 4.Производная постоянной равна нулю, т.е. если y=C, где С=const, то y'=0.
Теорема 5.Постоянный множитель можно выносить за знак производной, т.е. если y=Cu(x), где С=const, то y'=Cu'(x).
Пример 1.
Найдите производную функции
![]() .
.
Решение.
Данная функция имеет вид
![]() ,
гдеu=x,v=cosx. Применяя правило
дифференцирования (4), находим
,
гдеu=x,v=cosx. Применяя правило
дифференцирования (4), находим
![]() .
.
Пример 2.
Найдите производную функции
![]() .
.
Решение.
Применим формулу (5).
Здесь
![]() ;
;![]() .
.

![]() .
.
Задачи.
Найдите производные следующих функций:
![]() ;
;
11)![]()
2)![]() ;
12)
;
12)![]() ;
;
3)![]() 13)
13)![]()
4)![]() 14)
14)![]()
5)![]() 15)
15)![]()
6)![]() 16)
16)![]()
7)![]() 17)
17)![]()
8)![]() 18)
18)![]()
9)![]() 19)
19)![]()
10)![]() 20)
20)![]()
