книги из ГПНТБ / Пластическое деформирование металлов [сборник статей]

И . А. К РА В Ч Е Н К О , В. И. О ВЧИ Н Н И КО В

ПРИМЕНЕНИЕ РАСЧЕТНЫХ МЕТОДОВ И РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ В УСЛОВИЯХ ПРОИЗВОДСТВА

Результаты исследования смешанного режима трения, выпол­ ненные в лабораторных условиях с применением в качестве пла­ стической среды свинца, а в качестве смазки смеси канифоли и касторового масла, моделируют процессы горячей штамповки с применением стеклосмазок.

Характерной особенностью этих процессов является изотер­ мический режим, слабое упрочнение нагретого сплава и вязкие свойства расплавленной стеклосмазки.

Для проверки расчетного метода и достоверности моделиро­ вания были проведены производственные эксперименты.

В производственных условиях использовались в качестве пла­ стической среды круглые образцы из жаропрочного и титанового

ЦДМПУ-200 усилием 200 Т, на которой установлено нагреватель­ ное устройство УИДИН, обеспечивающее деформирование в изотермических условиях. Скорость движения верхнего ползу­ на этой машины — 1—2 мм/сек.

Особенность установки состоит в том, что она снабжена индук­ тором, который нагревает штамп и заготовки в межштамповом пространстве до температуры 1000° С. Поэтому деформирование заготовок происходит с постоянной температурой, а смазки дей­ ствуют при постоянной вязкости.

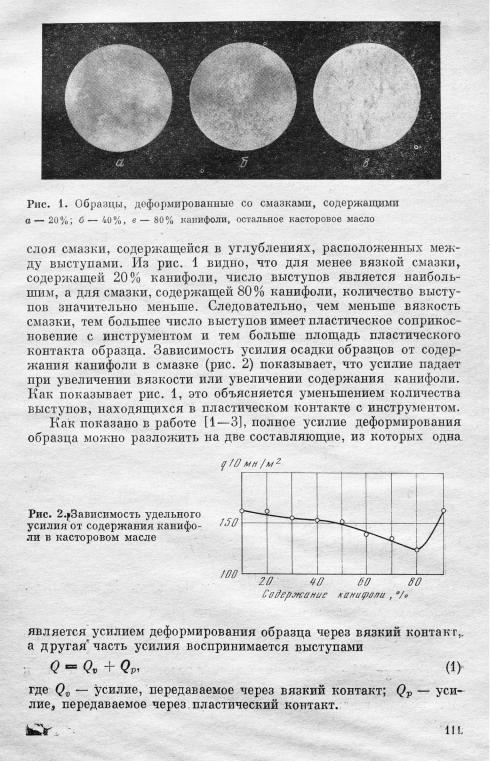
Основные предположения для вязко-пластического контак­ та. В процессах пластического формообразования смазочный слой работает в сложных условиях. Как будет показано далее, вязкий режим смазки может быть обеспечен только при создании доста­ точного давления смазочного слоя, например в случае гидро­ статического прессования. Если давление смазочного слоя нерегулируется, то при обычных условиях смазка выдавливается полностью или частично. На рис. 1 показаны образцы, которые деформировались со смазками, содержащими 20, 40, 80% канифо­ ли, остальное касторовое масло.

На поверхности образцов видны выступы и углубления, где задерживалась смазка. Высота выступов, образованных на

тическая толщина вязкого слоя является средней толщиной

110

Вследствие малого трения, усилие, передаваемое через вязкий

Определим усилие деформирования выступов.

Усилие, приходящееся на один выступ, вычисляется по полю линий скольжения, показанного на рис. 3. Со стороны смазки, находящейся между выступами, на поверхность BE действует контактное давление оп, которое равно о„ = 2к, где &=const — пластическая постоянная материала образца.

Гидростатическое давление в области ВОЕ равно [4]

Гидростатическое давление в области АСВ определяется по формуле

<зс = ° d — 2/сф = — к ( 3 + 2ср),

Так как линии скольжения подходят к поверхности АВ под углом я/4, то усилие, приходящееся на один выступ, равно

где Qt — усилие деформирования одного выступа; St — площадь соприкосновения одного выступа с поверхностью инструмента. Усилие деформирования всех выступов равно

П

S..

где С = ——■ 1 — отношение площади пластического контакта к

О

полной поверхности деформируемого образца; S — nd2/4 — полная площадь образца; d — диаметр образца.

112

Из формулы (6) можно определить отношение площади пласти­ ческого контакта к полной поверхности образца

рQ ~ 2 k S

В случае гидростатического режима смазки полное усилие равно

Q=

иотношение площади пластического контакта к полной поверхно­ сти деформируемого образца

nd2

S 2 —7— 2 к — knd2

Рис. 3. Смешанный режим трения

Рис. 4. Влияние угла ф и со­ става смазки на поверхность пластического контакта

Зная полное усилие при осадке образцов для смазок с различ­ ным содержанием канифоли по формуле (7) можно определить площадь пластического контакта образца с инструментом.

На рис. 4 показана вычисленная по формуле (7) зависимость отношения площади пластического контакта от значений угла О ^ Ф ^ я/2 для различного содержания канифоли и масла в смазке (табл. 1).

Как видно из этого графика, наименьшую площадь пластиче­ ского контакта имеет смазка с содержанием 80% канифоли и 20% масла. Кривые для смазок с содержанием канифоли 10 и 90% совпали. Это объясняется тем, что для жидкой смазки с 10% ка­ нифоли большая часть этой смазки вытекла и образец имеет боль­ шую площадь пластического контакта с инструментом.

Смазка, содержащая 90% канифоли, имеет высокую вязкость и с трудом деформируется. Усилие на деформацию этой смазки и образца требуется такое же, как и для смазки, содержащей 10% канифоли. '

Слой смазки, содержащей 90% канифоли, воздействует на образец, подобно инструменту. В этих условиях пластический кон­ такт, как показывает рис. 4, аналогичен контакту со смазкой, содержащей 10% канифоли. Площадь пластического контакта,

114

подсчитанная для различных жаропрочных образцов марки ЭИ437Б, деформирумых со стеклянными защитно-смазочными покры­ тиями при различных температурах, приведена в табл. 2.

Определение коэффициента пластического трения для смешан­ ного режима. Используя известную приближенную формулу [5], для осесимметричной осадки образца, можно выразить через пло­ щадь пластического контакта коэффициент трения Прандтля.

Действительно, формула [5] с коэффициентом трения Прандтля, заданным на поверхности инструмента, имеет вид

где / — коэффициент трения Прандтля; h — высота образца в метрах; S — площадь поверхности образца, л 2; d — диаметр образ­ ца; к — пластическая постоянная материала, Н1м2, приравняв правые части (6) и (8) получим

ным путем коэффициент пластического трения. Определив площадь пластического контакта, по рис. 4 для соответствующей смазки, можно определить угол ср. Затем, подставляя эти величины и геометрические размеры осаженного образца в правую часть (9),, получим значения пластического коэффициента трения.

Пластический коэффициент трения определяется следующим спо­ собом. Выбиралось значение угла ср. По формуле (7) определялось отношение С = Sp/S, затем по формуле (9) находили пластический

На рис. 5 показана зависимость коэффициента пластического трения для смазок с различным содержанием канифоли и масла. Из этого графика видно, что для смазки с содержанием канифоли 80% коэффициент пластического трения имеет наименьшее значе­ ние. Это объясняется тем, что площадь пластического контакта для этой смазки имеет наименьшее значение. Площадь пластического контакта для смазки с 10% канифоли имеет наибольшее значение и соответственно коэффициент пластического трения для этой

10 J 5, мм

Содержание епнифали, %

Рис. 5. Коэффициент пластического трения для различных смазок Рис. 6 . Зависимость критической толщины смазочного слоя от состава смазки

смазки наибольший. Смазка, содержащая 90% канифоли, очень вязкая и практически не деформируется, когда образец начал уже деформироваться. Таким образом, коэффициент пластического трения для смазки, содержащей 90% канифоли, имеет почти такое же большое значение, как и для смазки, содержащей 10% кани­ фоли.

Формула (9) замечательна тем, что она дает возможность увя­

1, чем больше значение этого коэффициента, тем лучше чистота поверхности. Задаваясь величиной С = Sp/S, по формуле (7) определяем необходимое усилие Q. Затем с заданной величиной С = Sp/S по формуле (9) определяем значение коэффициента пластического трения.

Значения коэффициента пластического трения для различных защитно-смазочных покрытий, подсчитанные по указанным форму­ лам, приведены в табл. 2.

Определение эффективности защитно-смазочных покрытий. Смазочные свойства характеризуются в основном следующими параметрами:

1)чистотой поверхности отштампованной детали;

2)критической толщиной смазочного слоя;

3)величиной усилия деформирования;

4)коэффициентом пластического трения.

Влияние смазки на процесс деформирования является весьма сложным, поэтому нельзя характеризовать смазку каким-то одним параметром. Каждый из перечисленных параметров характеризует одну из сторон смазочных свойств. Для оценки смазочных свойств требуется учитывать всю совокупность перечисленных пара-

116

метров. Например, для достижения наименьшего усилия при де­

Например, на рис. 1 показаны свинцовые образцы, обжатые со смазкой, содержащей 20 и 80% канифоли. Для первого из них удельное усилие является максимальным при наилучшей чистоте поверхности. Для второго удельное усилие минимальное, но чистота поверхности очень плохая. Для улучшения чистоты по­ верхности изделия (параметр 1 и 2) требуется увеличить усилие деформирования, параметр 3, при этом соответственно увеличи­ вается коэффициент пластического трения, параметр 4. Чистота поверхности определяется площадью пластического контакта изде­ лия и инструмента. Увеличение площади пластического контакта и уменьшение" толщины критического слоя улучшает чистоту поверхности и одновременно увеличивает коэффициент пластичен ского трения и усилие деформирования.

Для конкретного технологического процесса осадки круглой свинцовой заготовки с использованием смазок с различным про­ центным содержанием канифоли и масла параметр 1 определяется по рис. 4, параметр 2 определяется по рис. 6, параметр 3 определя­ ется по рис. 2, параметр 4 определяется по рис. 5.

Используя эти графики, можно выбрать такую смазку, пара­ метры которой являются оптимальными для данного техноло­ гического процесса.

Аналогичные расчеты производятся для процессов горячей штамповки с применением стеклосмазок, которые моделируются в лабораторных условиях.

Результаты производственных испытаний показаны в таблицах

ина графиках, приведенных выше.

Л И Т Е Р А Т У Р А

1.В. П. Звороно. Технология и нормативы холодного прессования продол­ говатых стальных изделий.— Сб. «Обработка металлов давлением». М.,. Изд-во АН СССР, 1958.

2.А. Д. Томленое. О вязкопластическом контакте в процессах формообра­

зования металлов.— Кузнечно-штамповочное производство, 1973, № 3.

3.А. Д . Томленое. Определение параметров смазочного слоя в процессах пластического формообразования металлов.— Сб. «Расчеты процессов пластического течения металлов». М., «Наука», 1973.

4.А. Д. Томленое. Теория пластического деформирования металлов. М., «Металлургия», 1972.

5.З.Зибель. Обработка металлов в пластическом состоянии. М., «Металлургиздат», 1934.

6* 117

в. в . ПОПОВ

0*НАПРЯЖЕНЯ0-ДЕФ0РМИР0ВАНН0М СОСТОЯНИИ ПРИ РЕДУЦИРОВАНИИ

Обычно исследование процесса редуцирования сводится к опре­ делению верхней оценки усилий деформирования кинематическим методом. Как показано в работе [1], конечное формоизменение круглого прутка может быть получено последовательными пере­ ходами плоской деформации. Это дает возможность для расчета усилий осесимметричного редуцирования применить ноля линий скольжения плоской деформации.

Однако для исследования локальных явлений, в частности причин возможных дефектов, необходимо построение полей на­ пряжений и скоростей на основе теории осесимметричного пла­ стического течения. В настоящей работе применена теория осе­ симметричного течения идеального жестко-пластического тела при условии пластичности Треска—Сен-Венана и ассоциированном законе течения. Использован пластический режим, соответствую­ щий ребру призмы Треска в пространстве главных напряжений.

Состояние материала при осесимметричном редуцировании характеризуется в цилиндрической системе координат (г, 0, z),

в пространстве главных напряжений (ох, а2, сг3), пластическое течение описывается дифференциальными уравнениями в частных производных гиперболического типа [2, 3]. Характеристики этих уравнений совпадают с направлениями максимальных касатель­ ных напряжений в меридиональной плоскости и определяются уравнениями

1(1 )

где а — угол между положительными направлениями оси г и характеристики \ первого семейства, отсчитываемый против ча­ совой стрелки. Характеристики первого | и второго ц семейства ортогональны и образуют первую систему криволинейных коор­ динат.

Дифференциальные соотношения для напряжений при условии

118

Компоненты напряжения в цилиндрических координатах свя­ заны с функциями р и а уравнениями

где

v^ — vT-cos a -f- vz sin a, v%— vzcos a — vrsin a — компоненты вектора скорости в направлениях характеристик.

Ассоциированный с ребром призмы Треска закон течения вы­ полняется, если справедливо неравенство [3]

При выполнении условия (5) диссипативная функция неотрица­ тельна [4].

Рассматриваемая задача является статически неопределимой и граничные условия для нее смешанные. Для построения реше­ ния применим численный метод решения задач осесимметричной деформации со смешанными граничными условиями [5].

Пусть на поверхности конической матрицы (рис. 1) известны контактные касательные напряжения хк к. Давление р на контуре матрицы представим в виде непрерывной вместе с первой производной функции р (s), где s — длина дуги контура матрицы, отсчитываемая от точки 20. Задача становится статически опре­ делимой. По уравнениям (1), (2) вычислим характеристики и функ­ ции р, а в областях 20—11—02, решая задачу Коши. Затем най­ дем характеристики и функции р, а в областях 20—11—10, 02— 11—01 (вырожденная задача Гурса) и в области 10—11—01—00 (задача Гурса). Углы в особых точках 20 и 02 определяются из условия пересечения оси симметрии характеристиками под уг­ лом 45°.

Скорость v0 жесткой области справа от характеристики 02—

Вдоль этих характеристик скорости при переходе из жесткой области в пластическую непрерывны, так как характеристики лересекакл ось симметрии [6]. Непрерывность скоростей на жестко­

119